Данный метод способствует уменьшению требуемого числа опытов. Приближенное решение уравнения (1) выберем в виде, удобном для аналитических преобразований:
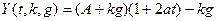(16)
Введём новую перемеренную состояния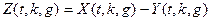 
,
отсюда
,
.
Выполним в уравнении (1) замену переменной X на Z:
(17)
Получим новое уравнение:
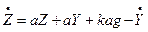, (18)
где 
, 
. (Учитывая, что A=0)
Оценка искомого математического ожидания определяется в виде (15), где первое слагаемое может быть найдено аналитически:
а второе слагаемое определяется по методу статистического моделирования на основе многократного решения полученного нового уравнения (18).
При удачном выборе функции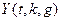 
дисперсия случайной величины 
оказывается существенно меньше, чем дисперсия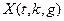 
что и приведёт к сокращению требуемого количества опытов.
Итак, по схеме итерационного алгоритма статистического моделирования, подробно рассмотренного выше, определим оценку математического ожидания величины Z.
Таблица 2 Результаты вычислений
| № итерации | mz | Dz | N треб. | Общее количество опытов |
| -0.2082 | 0.0138 | |||
| -0.2052 | 0.0136 | |||
| -0.2056 | 0.0135 | |||
| -0.2056 | 0.0134 |
В результате, при статистическом моделировании на основе использованного выше алгоритма, получили следующие оценки:
, 
, 
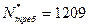
Оценка математического ожидания по (3) равна:
Таким образом, при использовании описанного метода позволило обеспечить снижение требуемого количества опытов по сравнению со стандартной схемой в 
раз. Программа, реализующая итерационный алгоритм, написана в среде MATLAB 6.5 [5]. Текст программы представлен в Приложении 2.
ЗАКЛЮЧЕНИЕ
В ходе выполнения работы были получены следующие результаты:
− определено математическое ожидание выходного сигнала неустойчивого апериодического звена в заданный момент времени, которое при решении задачи разными методами составило:
· при решении аналитически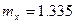 
;
· при решении прямым методом статистического моделирования 
(необходимо провести 21377 опытов);
· при решении методом выделения главной части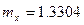 
(необходимо провести 1209 опытов);
− снижена трудоемкость статистического эксперимента в 17.7 раза за счет выбора и проведения исследования упрощенной модели.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Емельянов В. Ю. Методы моделирования стохастических систем управления. Учебное пособие. СПб, 2004.
2. Ануфриев И. Е. Самоучитель Matlab 5.3/6. x. СПб: БХВ-Петербург, 2002. 736 с.
3. “Положение о курсовых проектах и курсовых работах на факультете информационных и управляющих систем (общие требования)”.
ПРИЛОЖЕНИЯ
Приложение 1
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs,StdCtrls, Buttons;
type
TForm1 = class(TForm)
Memo1: TMemo;
Memo2: TMemo;
Edit1: TEdit;
Button1: TButton;
Memo3: TMemo;
Memo4: TMemo;
Memo5: TMemo;
Memo6: TMemo;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
const
alfa=9;
h=0.001;
eps=0.01;
kk=1200;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var
Sx,Sx2,mx,Dx,g,a,x,Sx2n,Sxn,mxn,Dxn,aa,kkk,K:real;
i,j,ll:integer;
ntreb,nn,n,n1,n2:longint;
flag:boolean;
begin
Sx:=0;
Sx2:=0;
randomize;
nn:=400;
Memo1.Lines.Clear;
Memo2.Lines.Clear;
Memo3.Lines.Clear;
Memo4.Lines.Clear;
Memo5.Lines.Clear;
Memo6.Lines.Clear;
// Начальная серия опытов
for i:=1 to nn do
begin
g:=1;
a:=random*0.6+0.5;
k:=random*0.4+0.6;
x:=0;
for j:=1 to kk do x:=(a*x+1*k*a)*h+x;
Sx:=Sx+x;
Sx2:=Sx2+sqr(x);
end;
mx:=Sx/nn; // Вычисление оценок МО и Дисперсии
Dx:=Sx2/(nn-1)-sqr(mx);
ntreb:=round(alfa*Dx/sqr(eps)); // Оценка Требуемого количества опытов
Memo1.Lines.Add('Mx='+FloatToStr(mx));
Memo1.Lines.Add('Dx='+FloatToStr(Dx));
Memo5.Lines.Add('ntreb='+FloatToStr(ntreb));
Memo6.Lines.Add('Sx='+FloatToStr(Sx));
Memo6.Lines.Add('Sx2='+FloatToStr(Sx2));
Memo5.Lines.Add('nn='+FloatToStr(nn));
n1:=0;
flag:=true;
// Дополнительная серия опытов
randomize;
while nn<ntreb do
begin
n1:=ntreb-nn; // Объём дополнительной серии
edit1.text:=floattostr(n1);
if (n1>8500) then n1:=n1 div 2
else begin
if n1<7 then n1:=n1*2;end;
for i:=nn to n1+nn do
begin
G:=1;
a:=random*0.6+0.5;
k:=random*0.4+0.6;
x:=0;
for j:=1 to kk do x:=(a*x+1*K*a)*h+x;
Sx:=Sx+x;
Sx2:=Sx2+sqr(x);
end;
Memo2.Lines.Add('n1='+FloatToStr(n1));
mx:=(Sx)/(n1+nn); //
Dx:=(Sx2)/(n1+nn-1)-sqr(mx);
Memo3.Lines.Add('Sxn='+FloatToStr(Sx));
Memo3.Lines.Add('Sx2n='+FloatToStr(Sx2));
Memo2.Lines.Add('mx='+FloatToStr(mx));
Memo2.Lines.Add('Dx='+FloatToStr(Dx));
nn:=n1+nn;
ntreb:=round(alfa*Dx/sqr(eps)); //
Memo4.Lines.Add('nn='+FloatToStr(nn));
Memo4.Lines.Add('ntreb='+FloatToStr(ntreb));
Memo4.Lines.Add('************************');
end; end;
end.
Приложение 2
Функция a.m
function ret = g(t,x);
global A;
global G;
global a;
global k;
Y = (A + k * G)*(1+a*t*2)-k*G;
dY = a*k*2;
ret = k * a * G + a * x + a * Y - dY;
Скрипт-файл Main.m
clear all;
clc;
global A;
global G;
global a;
global k;
G = 1;
t = 1.2;
A = 0;
array = [500 700 900 1100];
n = 0;
index = 1;
disp('Итерация М.О. Дисперсия Треб. кол-во опытов Общее кол-во опытов');
ntr = array(1);
while (n < ntr && index < 5)
nn=array(index);
for i = (n+1):1:nn
k = unifrnd(0.6, 1.0);
a = unifrnd(0.5, 1.1);
[T,U] = ode23('g', t, 0);
tmp = U(size(U));
x(i) = tmp(1);
end;
Mx = sum(x) / nn;
Dx = sum(x.^ 2) / (nn - 1) - Mx ^ 2;
n = nn;
ntr = round(9 / 0.0001 * Dx);
d = [index Mx Dx ntr n];
fprintf('%5.0f %8.4f %8.4f %5.0f %5.0f\n',d);
index = index + 1;
end;
