1. ЛОГИЧЕСКИЕ ПЕРЕМЕННЫЕ И ОПЕРАЦИИ
Пусть множество 
. Элементы этого множества называются логическими значениями, а переменные, которые могут принимать логические значения ― логическими переменными.
На множестве 
можно определить следующие логические операции.
― 0-арные (нольместные ) операции:
– константа 0; (1.0)
– константа 1. (1.1)
― 1-арные (одноместные) операции:
– повторение
(1.2)
– отрицание
(1.3)
― 2-арные (двухместные) операции:
– конъюнкция
; (1.4)
– импликация
; (1.5)
– отрицание импликации
; (1.6)
– сложение по модулю 2
; (1.7)
– дизъюнкция
; (1.8)
– стрелка Пирса
; (1.9)
– эквивалентность
; (1.10)
– штрих Шиффера
; (1.11)
Выражения 0, 1, 
, 
, 
, 
, 
, 
, 
, 
, 
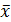называются простейшими логическими выражениями (формулами).
С помощью операции суперпозиции из простейших логических формул можно построить сложные логические формулы. Операция суперпозиции заключается в замене переменных логического выражения другими формулами.
/* Пример 1.1
Если в простейшую формулу
подставить
,
,
то получим сложную логическую формулу
.
Полученную формулу, в свою очередь, можно использовать для построения еще более сложной формулы, например, такой
. */
2. БУЛЕВЫ ФУНКЦИИ
Функция 
называется булевой, если она при любом значении аргумента принимает значения 0 или 1:
, 
(
).
Область определения логической функции
(
раз).
Элементы этого множества – кортежи (n- ки) 
, которые в математической логике называются словами и обозначаются строкой символов
или столбцом символов
.
Количество слов конечно и равно 
.
/* Пример 2.1
При:
существуют два слова: 0, 1;
― четыре слова: 00, 01, 10, 11;
―восемь слов: 000, 111, 001, 101, 010, 011, 100, 110. */
Каждому слову можно сопоставить целое число (номер слова)
. (2.1)
/* Пример 2.2
Номер слова 01 0101 равен
. */
Номера слов устанавливают на множестве слов 
идеальный строгий порядок:слово с меньшим номером предшествует слову с большим номером. Другими словами, множество слов можно упорядочить по возрастанию их номеров.
/* Пример 2.3
При 
упорядоченное множество слов следующее: 000 (номер 0), 001(1), 010(2), 011(3), 100(4), 101(5), 110(6), 111(7). */
Область значений булевой функции
.
Количество булевых функций конечно и равно 
. Это количество быстро возрастает с увеличением n.
/*Пример 2.4
При:
существуют 4 булевы функции 1-ой переменной;
―16функций 2-х переменных;
―256функций 3-х переменных;
―больше 4-х миллиардов функций 5-ти переменных. */
Булевой функции n переменных можно сопоставить число (номер функции)
, (2.2)
где 
― значение функции на слове с номером 0, 
― на слове с номером 1 и т. д.
Номера функций n переменных устанавливают на их множестве идеальный строгий порядок:функция з меньшим номером предшествует функции с большим номером.
Номера 
полностью определяют булевы функции и, в частности, позволяют строить таблицы истинности (таблицы истинности ― один из способов представления булевых функций).
/*Пример 2.5
Таблица истинности функции 
, с учетом того, что 
, имеет вид
.
или в более короткой форме записи
,
(в первой строке указаны номера слов в десятичной системе счисления, а во второй ― значения функции на этих словах). */
