3.1. Сечение цилиндра фронтально-проецирующей плоскостью

| Сечением цилиндра наклонной плоскостью является эллипс. Последовательность построения линии пересечения: 1. Выбираем опорные и промежуточные точки: 1 и 7 – точки пересечения очерков цилиндра с секущей плоскостью; 4 – точка границы видимости на профильной проекции; 2, 3, 5, 6 – промежуточные точки. 2. Строим фронтальную проекцию Г2 секущей плоскости уровня, проходящей через точку 32. пересекающей цилиндр по окружности. 3. Строим 31 горизонтальную и профильную 33 проекции точки 3. 4. Строим горизонтальные и профильные проекции других точек. 5. Соединяем полученные точки на профильной проекции плавной кривой (эллипс). |
3.2. Сечение призмы фронтально-проецирующей плоскостью

| Сечением шестигранной призмы наклонной плоскостью является шестиугольник. Последовательность построения линии пересечения: 1. Определяем на фронтальной проекции точки пересечения секущей плоскости Т с шестью ребрами пирамиды (точки 12,22,32,42,32',22'). 2. Достраиваем горизонтальные и профильные проекции этих точек. |
Таблица 3
Пошаговое построение овала для прямоугольной изометрии
| Последовательность построения овала в прямоугольной изометрии в плоскости П1: – проводим оси для изометрии и направление большой оси эллипса, перпендикулярное оси z; – описываем окружность заданным радиусом, из точки О пересечения изометрических осей, которая пересекает изометрические оси в точках 1, 2, 3, 4, 5 и 6; | 
|
| – проводим дуги из точек 5 и 6 радиусом R1= 63 = 51; | 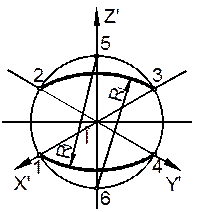
|
| – проводим прямые 62 и 63, которые пересекают большую ось эллипса в точках 7 и 8. Эти точки будут центрами дуг сопряжения, замыкающими овал; | 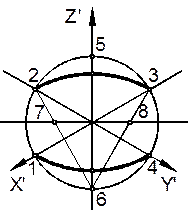
|
| – проводим замыкающие дуги из центров 7 и 8 радиусом R2 = 72 = 83 между точками сопряжения 1 и 2, 3 и 4. | 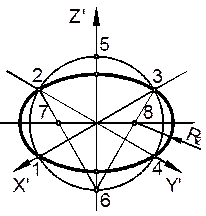
|
Таблица 4
Пошаговое построение овала для прямоугольной диметрии
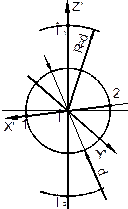
| Последовательность построения овала в прямоугольной диметрии в плоскости П1: – проводим оси для диметрии и направление большой оси эллипса, перпендикулярное оси z; – описываем окружность радиусом, равным радиусу заданной окружности из точки О пересечения осей, которая пересекает ось ОХ' в точках 1 и 2 и окружность радиусом равным диаметру заданной окружности, которая пересекает ось ОZ' в точках О1 и О2; |

| – проводим из точек О1 и О2 дуги радиусом R1=О11=О22; |
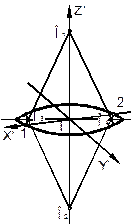
| – соединяем прямыми точку О1 с точкой 1 и точку О2 с точкой 2. На пересечении прямых с большой осью овала, получим точки О3 и О4, которые являются центрами замыкающих дуг эллипса; |

| – строим из центров О3 и О4 замыкающие дуги радиусом R2=О31=О42. |
Таблица 5






