На рис. 31 схематически показана лабораторная установка, с помощью которой исследуются закономерности поступательного и вращательного движения тел, необходимые для вычисления момента инерции системы.
Маховик 1 насажен на вал 2, который закреплен в шарикоподшипниках 3, 4, что обеспечивает вращение системы вокруг горизонтальной оси. На этом валу закреплены два шкива большего 5 и меньшего 6 диаметров. Диаметры шкивов измеряются штангенциркулем. На ободе каждого шкива имеется штырь для крепления нити с грузом.
На один из шкивов наматывается невесомая и нерастяжимая нить, к свободному концу которой прикрепляется груз 7 массой m. Положение груза относительно пола, т. е. высота h, измеряется длинной линейкой с миллимет
 |
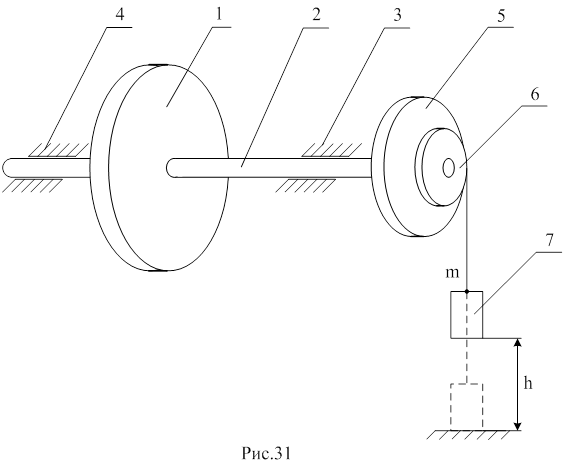ровыми делениями.
Измерение времени движения груза 7 до пола осуществляется секундомером.
Для вывода расчетной формулы момента инерции системы могут быть использованы динамический или энергетический подходы. В данном случае предлагается вывод, основанный на законе сохранения и превращения механической энергии.
Пусть груз массой m (рис. 31) находится в покое на высоте h над горизонтальной поверхностью (на высоте h от пола).
Из кинематики равноускоренного движения материальной точки имеем:
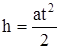и 
.
И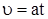сключая из последних выражений ускорение a, выразим скорость груза v непосредственно перед ударом его о пол:
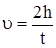, (8)
где t - время движения груза с высоты h.
В отсутствие проскальзывания нити можно использовать известную связь между модулями линейной и угловой скоростей:
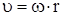, (9)
где r - радиус шкива, на который намотана нить с грузом;
u - линейная скорость точек на ободе этого шкива.
Из (8) и (9) получаем выражение для угловой скорости* (шкива, маховика, всей системы) в момент времени t касания груза массой m о пол:
. (10)
При расчете момента инерции системы необходимо учитывать влияние силы трения в подшипниках крепления вала.
В начальный момент система находится в покое, и груз массой m расположен на высоте h от пола. Следовательно, перед началом движения система обладает энергией, равной потенциальной энергии груза, т. е.
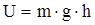. (11)
Если систему предоставить самой себе, то груз массой m будет равноускоренно опускаться, а маховик со шкивами приходить во вращательное движение.
В момент касания грузом пола потенциальная энергия груза переходит в суммарную кинетическую энергию системы и в работу против силы трения в подшипниках:
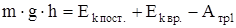, (12)
где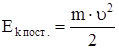 
- кинетическая энергия груза к моменту достижения пола;
- кинетическая энергия вращательного движения маховика со шкивами к моменту достижения пола грузом;
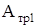- работа силы трения за n1 оборотов (число оборотов маховика от начала движения груза с высоты h до пола).
Уравнение (12) можно представить в виде:
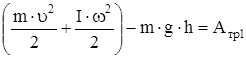. (13)
_____________
*Напомним, что любая точка твердого тела, вращающегося вокруг неподвижной оси, имеет одну и ту же угловую скорость.
**При вращении твердого тела вокруг неподвижной оси с угловой скоростью w i - ая частица тела, отстоящая от оси вращения на расстояние ri, обладает линейной скоростью
ui = wri (см. формулу (9)). Значит, кинетическая энергия этой частицы равна:
Екi =mi×ui2/2 = w2×mi×ri2.
Суммируя последнее выражение, получим кинетическую энергию всего тела:
Ек = åЕкi = w2×åmi×ri2/2.
С учетом (1) получим формулу кинетической энергии твердого тела, вращающегося вокруг неподвижной оси: Еквр. = Iw2/2.
После падения груза на пол и соскальзывания нити со шкива маховик продолжает вращаться до полной остановки. Это означает, что кинетическая энергия вращающегося маховика полностью перешла в работу силы трения, т.е.
, 
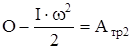. (14)
где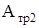 
- работа силы трения за n2 оборотов, т. е. до полной остановки маховика.
Работа силы трения (13) и (14), как неконсервативной (или диссипативной) силы, как правило, отрицательна и в условиях данного эксперимента пропорциональна числу оборотов, совершенных маховиком на первом и втором этапах:
, 
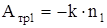, (15)
где k - положительный коэффициент, имеющий одно и то же значение в обоих случаях, и который можно представить с учетом (14) в следующем виде:
, 
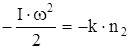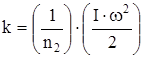. (16)
Тогда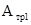 
(15) с учетом (16) определяется следующим выражением:
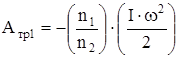. (17)
Уравнение (13) с учетом (17) принимает вид:
.
Преобразуя последнее равенство, получим с учетом (9) и (10) формулу расчета момента инерции системы:
,
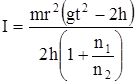которую можно упростить, учитывая, что 
>>2h и радиус шкива 
.
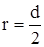Итак, расчетная формула момента инерции системы принимает окончательный вид:
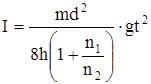, (18)
где d - диаметр шкива.
Порядок выполнения работы
Ход работы:
1) Таблица с экспериментальными вычислениями для большого шкива.
Таблица 1
| h = 82мм; Dh = 2мм; n1 = 4 | |
| N | d, мм |
| 65,4 | |
| 65,7 | |
| 64,6 | |
| 65,6 | |
| 65,6 | |
| Среднее <d> | 65,6 |
| S (<d>) | |
| Ddсл. | 0,39 |
| Ddпр. | 0,5 |
| Dd | 0,634 |
| Ed, % | 0,59 |
Таблица 2
| Dtпр. = 0,06; Dtсуб. = 0,15 | ||
| N | t, с | n2 |
| 8,67 | ||
| 8,64 | ||
| 8,8 | ||
| 8,69 | ||
| 8,81 | ||
| Среднее | <t> = 8,68 | <n2> =15 |
| S (<t>) | ||
| Dtсл. = 0,0852 | Dnсл. =1/4 | |
| Еt=0,98% | En=2% |
, 
, 
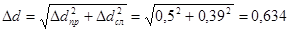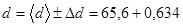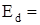0,59 %.
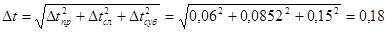с,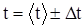 
=8,68+0.15; 
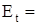0,98%.
, 
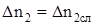=15+1/4об.
Среднее значение момента инерции маховика <I>:
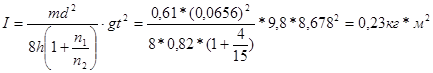
Относительная погрешность DI/I по формуле:
,
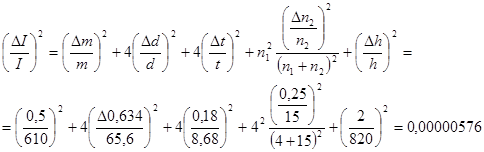где m = 610 г - масса груза;
Dm = 0,5 г - абсолютная погрешность измерения массы груза.
=0,361
Абсолютная погрешность DI=0,361*I=0.361+0,23=0,08303.
Конечный результат в стандартном виде
I = <I> ± DI = <0,23> ± 0,08330.
2) Таблица с экспериментальными вычислениями для маленького шкива.
Таблица 1
| h = 76,5мм; Dh = 2мм; n1 = 6 | |
| N | d, мм |
| 40,5 | |
| 39,5 | |
| 40,3 | |
| 39,6 | |
| 40,1 | |
| Среднее <d> | |
| S (<d>) | |
| Ddсл. | 0,415213 |
| Ddпр. | 0,05 |
| Dd | 0,646307 |
| Ed, % | 1,61576 |
Таблица 2
| Dtпр. = 0,005; Dtсуб. = 0,2 | ||
| N | t, с | n2 |
| 14,72 | 12,5 | |
| 14,51 | 12,5 | |
| 14,78 | 12,5 | |
| 14,44 | 12,5 | |
| 14,63 | 12,5 | |
| Среднее | <t> = 14,616 | <n2> = 12,5 |
| S (<t>) | ||
| Dtсл. = 0,2 | Dnсл. = 1/4 | |
| Еt = 1,65% | En = 2% |
, 
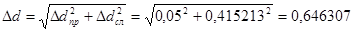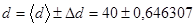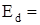, 1,045533%.
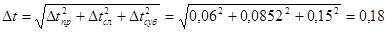с, 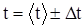=14,616+0,18; 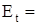0,98%.
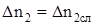, =12,5+1/4об.
Среднее значение момента инерции маховика <I>:
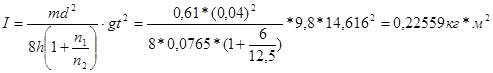
Относительная погрешность DI/I по формуле:
,
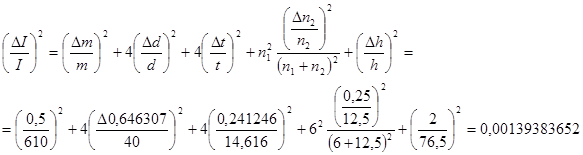где m = 610 г - масса груза;
Dm = 0,5 г - абсолютная погрешность измерения массы груза.
=0,0373341201
Абсолютная погрешность DI=0,0373341201*I=0,0373341201*0,22559=0,00843377773.
Конечный результат в стандартном виде
I = <I> ± DI = <0,22559> ± 0,00843377773.
