Лекция 9. Моды оптических резонаторов

Формирование стоячих волн в резонаторе. Согласно (6.13), добротность резонатора тем выше, чем выше время жизни фотона в моде. Это означает, что колебание на частоте будет существовать достаточно долго, если соответствующее значения достаточно велико. Это возможно, если электромагнитное поле на этой частоте имеет стационарное (устойчивое) распределение внутри резонатора. Как отмечалось выше, такое стационарное распределение поля и называют модой резонатора или его типом колебания.

Рассмотрим условие, при котором в резонаторе возможно формирование, стоячей волны.

Как известно, в бегущей волне векторы и совпадают по фазе (рис. 6.4), причем для векторов , и 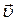всегда выполняется правило правого винта, где 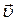– вектор скорости волны. Пусть эта волна распространяется внутри резонатора таким образом, что вектор ее скорости совпадает с осью . Представим изменение напряженностей электрического и магнитного полей этой волны в виде

 

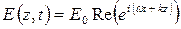, . (6.32)

 

Поскольку показатель преломления отражающих поверхностей зеркал всегда больше показателя преломления граничащей с ними внутрирезонаторной среды, то, как известно, при отражении от таких поверхностей вектор меняет фазу на , а вектор – не меняет совсем. Это же справедливо и для отражения волны от металлических поверхностей. На рис. 6.5 показаны направления векторов и в падающей на отражающую поверхность и отраженной волне.

Таким образом, внутри резонатора поле в каждой точке определяется следующей суммой прямой и обратной волн:

 

(6.33)

(6.34)

 

Полагая для простоты, что , , преобразуем эти выражения к виду:

, (6.35)

. (6.36)

 

Интенсивность электромагнитных волн определяется вектором Умова-Пойнтинга:

. (6.37)

 

Подставляя (6.35) и (6.36) в (6.37), получаем абсолютную величину этой интенсивности:

(6.38)

 

Нетрудно видеть, что формула (6.38) описывает стоячую волну. Действительно, в точках

 

, (6.39)

 

 

где , интенсивность рассматриваемой волны обращается в ноль, а между ними она принимает ненулевые значения.

Это означает, что вся ось резонатора поделена на отрезки длиной , в которых и сосредоточена энергия волны. Поскольку строго фиксированы, то эта энергия не может распространяться, она как бы локализована в пространстве четвертьволновых отрезков, что характерно только для стоячей волны. Точки оси резонатора, определяемые условием (6.39), принято называть узлами стоячей волны, а пространство между ними – ее пучностями.

Таким образом, в стоячей волне, в отличие от бегущей, векторы и сдвинуты относительно друг друга по фазе на (рис. 6.6)

 

Частотный спектр мод плоскопараллельного оптического резонатора (приближенная теория). Особенностью мод резонатора является то, что каждая из них может быть возбуждена без возбуждения других, т.е. независимо от них. Однако, как показано в теории электромагнитных волн, такая независимость (ортогональность) справедлива лишь в идеальном случае, когда зеркала резонатора обладают бесконечной проводимостью и имеют точную геометрическую форму. Отклонение от этих условий и учет наличия внутри резонатора активной среды могут привести к взаимодействию между модами, т.е. к трансформации энергии из одной моды в другие, в результате чего частотный спектр лазерного излучения может существенно измениться. При дальнейшем рассмотрении мы ограничимся случаем пустого резонатора с зеркалами точной геометрической формы (круг или прямоугольник) и с отражающей поверхностью, обладающей бесконечной проводимостью.

Рассмотрим сначала пустой прямоугольный закрытый резонатор с размерами, указанными на рис. 6.7. Если резонатор заполнен излучением, то оно принимает равновесное распределение, при этом задача о собственных колебаниях сводится к решению векторного волнового уравнения для поля при условии обращения в нуль его тангенциальной составляющей на стенках резонатора. В случае, когда объемный резонатор представляет прямоугольный параллелепипед, используют декартову систему координат, в которой переменные векторного волнового уравнения допускают разделение. Можно показать (решение оставляем за рамками настоящего курса), что составляющие вектора напряженности электрического поля излучения в резонаторе имеют вид:

 

(6.40)

 

Здесь , , 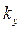– компоненты волнового вектора : , причём граничное условие фиксирует величины этих компонент

, , , (6.41)

 

где – целые положительные числа. Резонансные частоты, т.е. частоты собственных типов колебаний объемного резонатора, определяются формулой

 

. (6.42)

 

Соотношение (6.42) выражает условие образования стоячей волны при ее отражениях от стенок резонатора, а m, n, q определяют число полуволн, укладывающихся вдоль сторон 2 а, 2 а и L.

Электромагнитные колебания в объемном резонаторе, в отличие от электромагнитных волн свободного пространства, не являются поперечными: один из векторов или имеет проекцию на направление распространения волны – продольную составляющую. Если продольную составляющую имеет вектор , то электромагнитное колебание (моду объемного резонатора) называют электрическим и обозначают Е_mnq или ТМ_mnq (Transverse Magnetic). Если продольную составляющую имеет вектор , то электромагнитное колебание называют магнитным и обозначают H_mnq или ТE_mnq (Transverse Electric). Каждое колебание характеризуют тремя индексами m, n и q, соответствующими числу полуволн в направлениях x, y и z.

Плоскопараллельный оптический резонатор можно образовать из закрытого прямоугольного, если удалить боковые стенки. При этом в открытом резонаторе возможно существование только тех мод закрытого резонатора, которые распространяются вблизи оси . Другими словами, выражение (6.42) будет справедливо и для частотного спектра мод открытого резонатора, если положить, что в нем выполняется условие

 

. (6.43)

 

Данное предположение имеет свое физическое обоснование. Действительно, чем больше у моды индексы и , тем под бόльшим углом к оси резонатора направлены плоские волны, суперпозиция которых дает эту моду. Следовательно, тем большие дифракционные потери на краях зеркал испытывают эти волны, т.е. тем труднее будут возбуждаться соответствующие моды.

Таким образом, полагая второй член под корнем в выражении (6.42) много меньшим единицы и разлагая это выражение в степенной ряд, получим частотный спектр мод для плоскопараллельного резонатора с прямоугольной конфигурацией зеркал:

 

. (6.44)

 

Отсюда следует, что для каждого набора трех чисел m, n, q существует вполне определенная мода резонатора с вполне определенной резонансной частотой. Индекс q равен числу полуволн моды, укладывавшемуся на длине резонатора L, и называется продольным или аксиальным индексом, а индексы m и n обозначают число изменений знака поля на поверхности зеркал и называются поперечнымииндексами.

Обозначение и классификация мод. Об обозначении мод в закрытом резонаторе говорилось выше. В открытом оптическом резонаторе собственные электромагнитные колебания имеют пренебрежимо малые проекции и на ось резонатора z. Их обозначают аббревиатурой (Transverse Electric and Magnetic). Поскольку в лазерных резонаторах значение индекса всегда очень велико, то его часто не указывают, и моды обозначают только поперечными индексами – .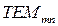

Введение таких обозначений наложило соответствующий отпечаток и на классификацию мод лазерных резонаторов. Суть этой классификации такова:

Мода, у которой поперечные индексы фиксированы, а продольный индекс является произвольным, называется поперечной модой. Она включает в себя столько типов колебаний резонатора, сколько значений принимает продольный индекс . Другими словами, поперечная мода имеет не одну резонансную частоту, а, согласно (6.44), несколько частот.

Мода, у которой все индексы фиксированы, называется продольной (или аксиальной) модой. Она имеет единственную резонансную частоту и является одной из компонент поперечной моды с теми же фиксированными поперечными индексами. Поэтому, говоря о продольной моде, следует указывать поперечную моду, которой она принадлежит.

Каждая мода характеризуется определенной пространственной структурой поля (определенным распределением амплитуды и фазы) в поперечном к оси резонатора направлении, в частности на поверхности зеркал резонатора.

Поперечная мода с нулевыми поперечными индексами обозначается как 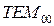и называется основной поперечной модой. Она обладает рядом привлекательных свойств и имеет большое значение в лазерной физике и технике и их различных практических приложениях.

При обозначении поперечной моды 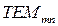резонатора с прямоугольными зеркалами на первое место ставится тот поперечный индекс (в данном случае ), который соответствует большей стороне прямоугольника зеркала. Другими словами, ось всегда следует выбирать по направлению большей стороны зеркала. Для круглых зеркал обозначение мод соответствует цилиндрической системе координат, поэтому здесь принято, что первый индекс соответствует числу изменений знака поля по радиусу зеркала, а второй индекс – числу изменений знака поля при повороте вокруг центра зеркала на 180°. Часто радиальный и угловой (азимутальный) индексы моды обозначают символами и , соответственно.

На рис. 6.8 представлен характер изменения знака амплитуды поля на поверхности зеркал квадратной (а) и круглой (б) формы для нескольких наиболее простых (низших) поперечных мод. Стрелками указано направление вектора электрического поля на поверхностях зеркал, а сами поверхности разбиты на области, в которых это направление одинаково. Стрелка с бóльшей длиной означает бóльшую амплитуду поля. В каждой области с одинаковым направлением поля формируется световое пятно. Соответственно, каждый тип поперечной моды имеет определенную структуру светового пятна на зеркале резонатора. На рис. 6.9 показана структура наблюдаемого светового пятна для нескольких низших поперечных мод на поверхности квадратного (а) и круглого (б) зеркал.

 

 

Чем бóльшие значения имеют поперечные индексы и , тем более высокий порядок имеет данная мода и тем большее число пятен наблюдается в соответствующей ей картине на поверхности зеркала.

Частотный спектр лазерного излучения в случае плоскопараллельного резонатора. В плоскопараллельном резонаторе частотный интервал между соседними продольными модами, принадлежащими одной и той же поперечной моде, во много раз превышает частотный интервал между двумя соседними поперечными модами. Чтобы в этом убедиться, достаточно вычислить эти интервалы и сравнить между собой. Действительно, из (6.44) следует, что частотный интервал между соседними продольными модами и равен

 

. (6.45)

 

Частотный интервал между соседними поперечными модами и

, (6.46)

 

а между соседними поперечными модами и

 

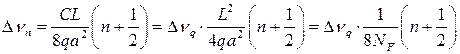, (6.47)

 

Отсюда следует, что

, . (6.48)

 

Поскольку для наиболее часто используемых лазерных резонаторов , а m и n имеют величину порядка нескольких единиц, то из (6.48) следует, что в плоскопараллельном резонаторе

 

(6.49)

 

т. е. сделанное утверждение можно считать доказанным. Для типичных значений L величины составляют порядка нескольких сотен мегагерц, тогда как (или ) – порядка нескольких мегагерц.

Отметим, что расстояние по частоте между аксиальными модами увеличивается при уменьшении длины резонатора L, а между соседними поперечными модами и – при уменьшении числа Френеля . Из (6.44) видно, что моды с одинаковыми q, но разными m и n, удовлетворяющими условию 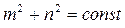, имеют одну и ту же частоту. Такие моды называют частотно вырожденными.

Для того чтобы определить, сколько резонансных частот будет одновременно присутствовать в выходном излучении лазера, необходимо знать ширину контура линии люминесценции рабочего перехода активной среды, так как именно эта ширина определяет тот спектральный диапазон, в пределах которого осуществляется лазерная генерация. Как отмечалось выше, в большинстве случаев ширина линии люминесценции много больше частотных интервалов между модами, т. е. выполняется условие

 

, (6.50)

 

и в спектре лазерного излучения наблюдается много мод.

На рис. 6.10 приведена качественная картина частотного спектра лазерного излучения при использовании плоскопараллельного резонатора. При этом следует помнить, что спектральные линии излучения, соответствующие модам резонатора, будут располагаться по всей ширине линии люминесценции только в том случае, если уровень накачки обеспечивает условие генерации по всему контуру усиления. Если же усиление будет больше потерь только в определенной области контура этой линии, то спектр излучения будет наблюдаться только в этой области.

Теория Фокса и Ли. Более строгое рассмотрение свойств оптических резонаторов должно базироваться на решениях уравнений Максвелла. Определение собственных колебаний сводится к отысканию стационарных решений соответствующей краевой задачи. Такой метод является наиболее точным, однако он приводит к чрезвычайно громоздким соотношениям. Более наглядный метод расчета характеристик оптических резонаторов основывается на принципе Гюйгенса-Френеля. Фоксом и Ли были предложены методы расчета характеристик плоскопараллельного резонатора, основанные на этом принципе. Т.е. они решали эту задачу в так называемом скалярном приближении, нередко используемом в оптике. Это приближение допустимо, если размеры зеркал велики по сравнению с длиной волны, электромагнитное поле предполагается почти поперечным и линейно поляризованным.

Пусть однородная плоская волна стартует от левого зеркала, направляясь к правому. По мере распространения некоторая доля энергии из-за дифракции уходит из периферийной области волны еще до того, как она достигнет правого зеркала. При отражении также ослабляется периферийная часть отражаемой волны. Отраженная волна, распространяясь справа налево, теряет энергию аналогичным образом. В результате многократного повторения поле на краях волнового фронта становится слабее.

При вычислениях произвольное начальное распределение поля у левого зеркала служит источником поля, возникающего у правого зеркала в результате первого прохода волны. Затем полученное распределение используется для точно такого же вычисления распределения поля, созданного у левого зеркала в результате второго прохода. Эти вычисления повторяются многократно для последующих проходов.

Поле волны можно записать в виде скалярной величины u, представляющей, скажем, амплитуду электрического (или магнитного) поля. Тогда, выражая поле у одного зеркала через поле у другого зеркала с помощью принципа Гюйгенса в форме Френеля- Кирхгофа, можно получить интегральное уравнение для искомой функции распределения поля на зеркале.

Действительно, поле 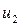в зоне Френеля на одном из зеркал, обусловленное излучением, отраженным от другого зеркала площади А, дается интегралом по поверхности А:

 

, (6.51)

 

где – поле на апертуре «излучающего» зеркала, – постоянная распространения в среде, r – расстояние от точки на «излучающем» зеркале до точки наблюдения, θ – угол, который вектор образует с нормалью к плоскости зеркала. После q проходов поле у одного зеркала связано с полем, отраженным другим зеркалом, формулой (6.51), в которой 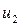надо заменить на , а на .

В стационарной стадии поля около зеркал становятся одинаковыми с точностью до комплексной постоянной. Можно записать, таким образом, что

 

, (6.52)

 

где 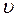– функция распределения, не изменяющаяся от отражения к отражению, a – комплексная постоянная, не зависящая от пространственных координат и характеризующая условия распространения излучения между отражениями. Подставляя (6.52) в (6.51), мы получаем интегральное уравнение

 

, (6.53)

ядро которого имеет вид

 

. (6.54)

 

Выражение (6.53) с учетом (6.54) представляет собой однородное интегральное уравнение Фредгольма второго рода. Уравнение не имеет аналитического решения. Вычисления проводились Фоксом и Ли методом итераций с помощью ЭВМ. В результате оказалось, что после многих (около 300) отражений действительно устанавливается стационарное распределение поля с уменьшающейся к краю зеркала амплитудой.

Собственные функции этого интегрального уравнения определяют распределения поля на зеркалах исследуемого резонатора. Важным свойством функций является их ортогональность. Физически это означает, что колебания, соответствующие различным значениям функции , т.е. различным распределениям амплитуды и фазы по поверхности зеркал, могут существовать независимо друг от друга. Собственные значения определяют затухание и фазовый сдвиг волны в течение каждого прохода, являясь, таким образом, постоянными распространения соответствующих мод. Логарифм имеет вещественную и мнимую составляющие

 

. (6.55)

 

Для каждого собственного колебания определяет затухание волны за один проход, а – фазовый сдвиг за один проход, добавленный к геометрическому фазовому сдвигу

В качестве примера на рис. 6.11 приведены результаты, полученные для амплитуды поля в случае, когда начальное распределение поля выбрано однородным и симметричным (т. е. = const). При N _F = 6,25, чтобы достичь стационарного решения, необходимо приблизительно 200 проходов. Аналогично антисимметричная мода низшего порядка получается в том случае, когда первоначальное распределение выбирается однородным и антисимметричным (т. е. 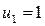при и при ). На рис. 6.12 представлены распределения поля , полученные таким методом для двух значений числа Френеля.

Результаты численного расчета резонансных частот плоскопараллельного резонатора, выполненного Фоксом и Ли, показали, что для достаточно больших чисел Френеля они хорошо согласуются со значениями, предсказанными соотношением (6.44). Например, для N _F > 10 расхождение не превышает 10 %.

 

 

 

Распределение поля внутри резонатора с плоскими зеркалами в разных сечениях, перпендикулярных оптической оси, изменяется незначительно. Это позволяет достаточно эффективно использовать активный объем рабочего вещества.

Недостатком плоского резонатора, с точки зрения его практического применения, является трудность юстировки: параллельность зеркал друг относительно друга должна быть выдержана с точностью до нескольких угловых секунд. Этого недостатка лишены резонаторы со сферическими зеркалами.

В заключение отметим, что Анализ Фокса и Ли, выполненный ими для открытых резонаторов типа интерферометра Фабри-Перо в нескольких геометрических конфигурациях (прямоугольные плоские зеркала, круглые плоские зеркала, конфокальные сферические и параболические зеркала), привел к следующим важным выводам:

1. Открытые резонаторы типа интерферометров Фабри-Перо как с плоскими, так и с вогнутыми зеркалами характеризуются дискретным набором колебательных мод.

2. Однородные плоские волны не являются нормальными модами открытых резонаторов.

3. Электромагнитные волны, соответствующие собственным модам резонатора, почти полностью поперечны. Поэтому моды обозначаются символом ТЕМ.

4. Моды более высокого порядка всегда имеют более высокие дифракционные потери, чем основная мода.

5. Для основной моды амплитуда поля сильно уменьшается к краям зеркала. Поэтому ее дифракционные потери много меньше предсказываемых на основе представления об однородных плоских волнах и в реальных ситуациях пренебрежимы.

Результаты Фокса и Ли показали плодотворность анализа полей и волн в открытых резонаторах путем решения интегральных уравнений, связывающих между собой поля на зеркалах резонатора на основе принципа Гюйгенса в интегральной форме Френеля -Кирхгофа.