1. Каждый график должен иметь четкое название, в котором указывается его содержание, время и место проведения исследования.
2. График строится в строго определенном масштабе.
3. Он должен содержать условные обозначения (продумать различные цвета или штриховку для их изображения).
4. Необходимо указывать единицы измерения используемых данных.
5. Избегать перегруженности цифровыми данными.
6. Выбор типа диаграмм должен быть адекватным сути статистических величин.
Для наглядного изображения интенсивных коэффициентов используются: линейные, столбиковые, ленточные, пирамидальные диаграммы.
Для наглядного изображения экстенсивных коэффициентов используются: внутристолбиковые, секторные диаграммы.
Цель построения статистических графиков – в первую очередь получение информации в наглядной и зрительно легко воспринимаемой форме. В частности, с помощью графиков можно проследить участки возрастания, убывания или стабильности каких-либо показателей.
Основными характеристиками статистического графика являются: поле, заголовок и легенда графика, масштабная шкала.
Полем графика называют объект, на котором воспроизводится график, будь то лист бумаги, географическая карта или экран компьютера.
Каждый график должен иметь свое название - заголовок, а также пояснение к его содержанию, называемое легендой графика.
Масштабной шкалой называют линию, на которой указан принятый масштаб. Масштабная шкала может быть как прямолинейной (числовая ось), так и криволинейной (например, окружность с масштабной единицей измерения в градусах).
Принято различать следующие основные типы графических изображений данных:
- диаграммы,
- картограммы,
- картодиаграммы.
Самым распространенным из них является диаграмма — изображение статистических данных посредством геометрических фигур либо символов.
Диаграммы чаще используются в медико-социальных исследованиях, в то время как картограммы и картодиаграммы — в медико-географических исследованиях.
Диаграммы можно классифицировать различным образом.
Так, по назначению принято различать диаграммы сравнения, структурные и динамические.
По форме отображения: линейные, столбиковые, ленточные, секторные круговые, секторные столбиковые, радиальные или диаграммы в полярных координатах, диаграммы рассеяния, слоевые и др.
Линейная диаграмма показывает динамику какого-либо статистического показателя (заболеваемости, смертности, рождаемости и др.). Нанесение разных показателей на график позволяет наглядно сравнить в динамике эти показатели.
В основе построения линейной диаграммы лежат две перпендикулярные линии: горизонтальная (ось абсцисс) и вертикальная (ось координат), образующие так называемую систему треугольных координат.
Точка пересечения вертикальной и горизонтальной линий служит пунктом отсчета.
На оси абсцисс откладывается время или любые факториальные знаки; затем из точек, соответствующих определенным моментам или показателям времени, восстанавливаются ординаты.
Вершины соединяются прямой прямыми линиями, и полученный график представляет собой линейную диаграмму.
Пример линейной диаграммы представлен на рис. 1.

Интенсивные показатели графически изображаются также в виде плоскостных диаграмм. К ним относятся – столбиковые и ленточные диаграммы. В виде столбиков целесообразно изображать интенсивные показатели для одного периода, но для разных заболеваний, территорий, коллективов или, наоборот, в разные периоды времени, но для одного заболевания, территории, коллектива.
При построении столбиковых диаграмм основание располагаются на оси абсцисс. На оси ординат отмечают величину изучаемого признака в принятом масштабе. Ширина столбиков должна быть одинаковой. Столбики могут располагаться как на расстоянии друг от друга, так и рядом друг с другом.
Столбиковые диаграммы могут быть:
· вертикальными (рис. 2)
· горизонтальными (тогда они еще называются ленточными).
·

Столбиковые диаграммы используют не только для изображения динамики интенсивных коэффициентов, но и для изображения статики явления и коэффициентов соотношения. Для построения столбиковой диаграммы рисуют столбики, высота которых соответствует величине изображаемых чисел. Для точного соблюдения масштаба слева проводят вертикальную линию, на которой указывают масштаб изображенного явления. Ширина всех столбиков и расположение между ними должны быть одинаковыми. Средние величины также удобнее показывать в столбиковой диаграмме.
Для характеристики сезонности какого-либо явления можно рекомендовать особый вид линейной диаграммы, построенной по системе так называемых полярных координат радиальную диаграмму (рис.3). Окружность делится на 12 секторов соответственно число месяцев в году, на которых откладываются величины, характеризующие явление. Масштабом является радиус, который равен среднегодовой величине изучаемого явления. Точки, отмеченные на радиусах и их продолжениях соединяют и получают многоуровневый график, отражающий изменения явления в течение года.

Рис.3. Радиальная диаграмма. Сезонность заболеваемости кишечными инфекциями (на 10 000 человек)
Для изображения экстенсивных показателей часто используют секторную диаграмму. Для построения секторной диаграммы окружность принимается за 100%, при этом 1% данного явления соответствует 3,6º окружности. Показатель явления в % умножается на 3,6°, что и дает величину окружности, которая откладывается при помощи транспортира и эти точки соединяются с центром круга.

ЗАДАЧА – ЭТАЛОН №1
Численность населения в Российской Федерации на 1 января 2012 года составляет 143056 тыс. человек, из них городское население составила 105718,38 тыс. человек, а сельское население составила 37337,61 тыс. человек.
Рассчитайте удельный вес городского и сельского населения Российской Федерации.
Решение.
Рассчитываем долю городского населения:
143056 тыс. человек – 100%
105718,38 тыс. человек – х
Х= 105718,38 х 100 = 73,9%
Рассчитываем долю сельского населения:
143056 тыс. человек – 100%
37337,61 тыс. человек – х
Х= 37337,61 х 100 = 26,1%
Выводы:
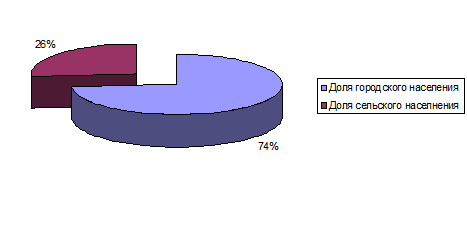
В структуре населения Российской Федерации на 1 января 2012 года удельный вес городского населения составляет 73,9%, а доля сельского населения составляет 26,1%.
Графические изображения можно представить секторной и внутристолбиковой диаграммами (рис. 3,4)
-
|
-

Рис. 6 Удельный вес городского и сельского населения в Российской Федерации на 1 января 2012 года.
ЗАДАЧА – ЭТАЛОН №2
Представить информацию о сезонных изменениях заболеваемости дизентерией в виде радиальной диаграммы (табл. 1)
Таблица 1
| Месяц | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | Всего |
| Число случаев |
Радиальная диаграмма состоит на основе окружности:
1) окружность делят при помощи транспортира на число секторов, соответствующее интервалам времени изучаемого цикла: 4 сектора при изучении явления за кварталы года, 7 секторов при изучении явления за дни недели, 12 секторов при изучении явления за год.
2) определяют среднемесячный уровень заболеваемости за год (ординар), который будет соответствовать длине радиуса окружности: (2+7+5+15+9+26+15+37+22+14+3+1)/12 = 13.
3) на каждом радиусе, соответственно каждому месяцу откладывают в выбранном масштабе число случаев заболевания дизентерией.
4) конечные точки отрезков соединяются линиями
5) полученный многоугольник изображает колебания числа случаев заболеваний дизентерией за данный период – 12 месяцев.
Вывод: Анализ радиальной диаграммы, изображенной на рисунке 7 позволяет увидеть значительное увеличение числа случаев заболевания дизентерией в летне-осенний период (с апреля по октябрь).
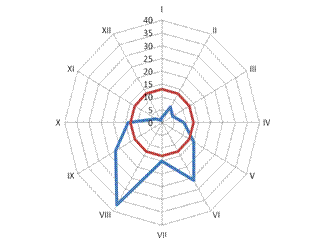
Рис. 7 Сезонные изменения числа случаев заболеваний дизентерией за изучаемый год в городе N
ЗАДАЧА-ЭТАЛОН №3
Рассчитать показатели наглядности для уровней госпитализации в больничные учреждения города А. в динамике за 5 лет наблюдения и представить графически.
Уровень госпитализации в больничные учреждения в города А. за последние 5 лет (на 100 человек населения)
Таблица 2
| Показатели | Годы | ||||
| Уровень госпитализации в городе А. | 24,4 | 22,8 | 21,2 | 20,5 | 20,7 |
| Показатель наглядности, % | 93,44 | 86,9 | 84,0 | 84,7 |
РЕШЕНИЕ
Снижение количества больных, поступивших в стационары, будет нагляднее, если приравнять показатель исходного уровня госпитализаций в городе А. (2009 – 24,4) за 100%, а остальные показатели пересчитать в процентах по отношению к нему.
| 24,4 - 100 % 22,8 - X | X = (22,8 х 100) / 24,4 = 93,44% | (показатель наглядности для 2010 года) |
| 24,4 — 100 % 21,2-X | X = (21,2 х 100) / 24,4 = 86,9% | (показатель наглядности для 2011 года) |
| 24,4 - 100 % 20,5 — X | X - (20,5 х 100) / 24,4 = 84% | (показатель наглядности для 2012 года) |
| 24,4 — 100 % 20,7 - X | X = (20,78 х 100) / 24,4 = 84,8% | (показатель наглядности для 2013 года) |
Вывод. В динамике за 5 лет наблюдения уровень госпитализации больных в городе А. снижается.
В 2013 году уровень госпитализации больных (в показателях наглядности)по сравнению с 2009 годом снизился на 15,2%.
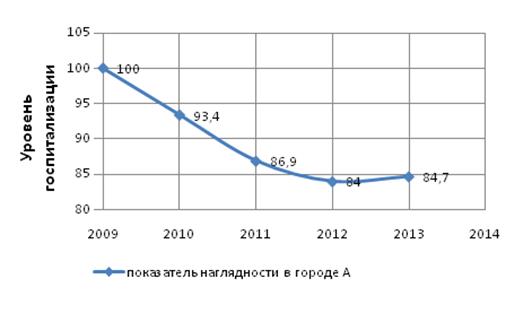
Рис 8. Линейная диаграмма уровня госпитализации в городе А. за 5 лет (в показателях наглядности)






