В О П Р О С 2
- Фундаментальные решения дифференциальных уравнений. Обобщенные и классические решения дифференциальных уравнений и связь между ними.



- Решения неоднородных дифференциальных уравнений. Свойства свертки фундаментальных решений.

- Фундаментальные решения линейного дифференциального уравнения с обыкновенными производными. Решения неоднородных уравнений.

- Уравнения Лапласа и Пуассона. Уравнения для потенциалов гравитационного и электростатического полей. Ньютоновские и кулоновские потенциалы.


- Фундаментальные и обобщенные решения уравнения Лапласа-Пуассона в пространстве размерности N=2. и их свойства.




6. Формулы Гаусса и Грина для решений уравнения Лапласа-Пуассона в пространстве размерности N=2.
Определение. Уравнение
 (1)
(1)
называется эллиптическим, если  ,
,  .
.
В этом случае  его каноническое выражение имеет вид:
его каноническое выражение имеет вид:

Уравнение Лапласа-Пуассона имеет вид:
 -эллиптическое уравнение.
-эллиптическое уравнение.
Если 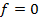 -уравнение Лапласа,
-уравнение Лапласа,  -Уравнение Пуассона.
-Уравнение Пуассона.
Определение.  (2)
(2)
 ,
, 
 -решение, где
-решение, где  ,
,  -фундаментальное решение
-фундаментальное решение
 (3)
(3)
N=2:  (плоскость)
(плоскость)
Вторая формула Грина в 

Классическая формула Грина
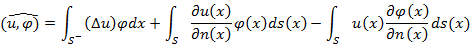


7.Фундаментальные и обобщенные решения уравнения Лапласа-Пуассона в пространстве размерности N=3. и их свойства.
мы знаем, что если имеется объемная  и поверхностная
и поверхностная  плотность заряда, то потенциал их может бытьзаписан в виде:
плотность заряда, то потенциал их может бытьзаписан в виде:
 (4.1)
(4.1)
Но такой путь не всегда целесообразен, т.к.:
а) иногда приводит к сложным вычислениям;
б) требует анализа, в случае если заряды не расположены в конечной области пространства и нормировки потенциала 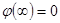 .
.
В этих случаях удобнее свести задачу о нахождении  к решению дифференциального уравнения. Найдем это уравнение:
к решению дифференциального уравнения. Найдем это уравнение:
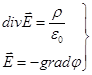

 , где
, где  , т.е.
, т.е.
 (4.2) - уравнение Пуассона, где
(4.2) - уравнение Пуассона, где
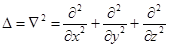 - оператор Лапласа.
- оператор Лапласа.
В области пространства, где нет зарядов 

 (4.3)- уравнение Лапласа.
(4.3)- уравнение Лапласа.
Решения уравнения (4.2) должны удовлетворять требованиям непрерывности и конечности  .
.
Преимущество нахождения  с помощью уравнения (4.2) заключаются в большей общности этого метода и его широкая применимость, т.к. уравнение Пуассона не предполагает определенной нормировки
с помощью уравнения (4.2) заключаются в большей общности этого метода и его широкая применимость, т.к. уравнение Пуассона не предполагает определенной нормировки  и отсутствия зарядов на бесконечности.
и отсутствия зарядов на бесконечности.
Если же все заряды  сосредоточены в конечной области пространства
сосредоточены в конечной области пространства  , то решением уравнения Пуассона будет:
, то решением уравнения Пуассона будет:
 , что
, что
следует из однозначности решения задач электростатики.
Б2. 8. Формулы Гаусса и Грина для решений уравнения Лапласа-Пуассона в Полнота  и R3.
и R3.




9.Уравнение теплопроводности. Закон Фурье. Фундаментальные решения уравнения теплопроводности и их свойства.









10.Обобщенные и классические решения уравнения теплопроводности в  и
и  . Тепловые потенциалы
. Тепловые потенциалы

11. Задача Коши для уравнения теплопроводности в пространствах разной размерности. Метод обобщенных функций Владимирова В.С.

12.Функционально-инвариантные решения Смирнова-Соболева волнового уравнения в  . Гармоническая волна и ее характеристики: волновой вектор, длина волны, частота, период, фаза.
. Гармоническая волна и ее характеристики: волновой вектор, длина волны, частота, период, фаза.


Упругая волна называется гармонической, если соответствующее ей колебание частиц среды является гармоническим.
Покажем зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени.
 – расстояние до источника
– расстояние до источника
 – смещение
– смещение

Длина волны – расстояние между ближайшими частицами, колеблющимися в одинаковой фазе.
 , где
, где  – скорость волны
– скорость волны
k – волновое число




13.Ударные волны как обобщенные решения волнового уравнения, волновые фронты. Условия Адамара на фронтах ударных волн.

14.Фундаментальные решения волнового уравнения и их свойства в пространствах  , N=1. Запаздывающие потенциалы.
, N=1. Запаздывающие потенциалы.
15.Фундаментальные решения волнового уравнения и их свойства в пространствах  , N=2. Запаздывающие потенциалы.
, N=2. Запаздывающие потенциалы.

Задача Коши для уравнения Даламбера в D’ (R’). Функция Римана. Метод обобщенных функций Владимирова В.С.
Задача: решить задачу Коши (уравнение математической физики, уравнение в частных производных гиперболического типа)
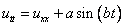
 ,
, 
Решение:
Для уравнения вида

с начальными условиями
 ,
, 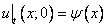
форму Даламбера имеет вид:

Подставим в эту формулу 

Далее следует простое интегрирование.

Ответ: 


17. Задача Коши для волнового уравнения в пространстве размерности N=2. Формулы Пуассона.








