Нейроинформатика
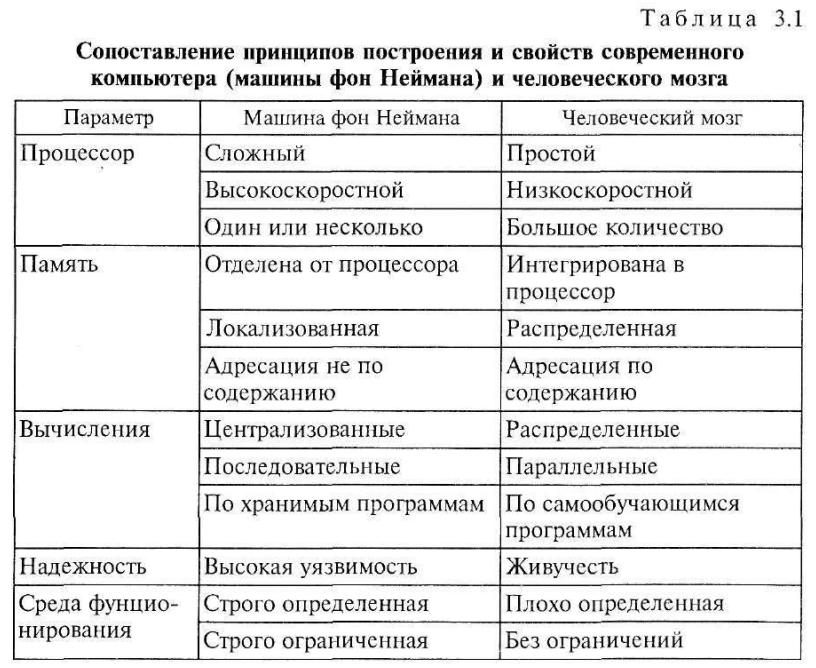
В рамках нейроинформатики рассматриваются устройства структурно и функционально подобные мозгу человека.
Поэтому схематично нейрон можно представить в следующем виде:
| Дендриты |
| Тело клетки |
| Аксон |
Выделим основные типы задач, успешно решаемых при помощи искусственных нейронных сетей в настоящее время:
1) аппроксимация функций (построение моделей трудно формализуемых зависимостей).
Предположим, что имеется обучающая выборка ((x1, y1), (x2, y2), …, (xn, yn)), представленная парами вход – выход, которая генерируется неизвестной функцией y = f(x), искаженной шумом.
Задача аппроксимации состоит в нахождении оценки неизвестной функции y = f(x), что используется при решении многочисленных инженерных и научных задач моделирования
2) классификация образов (задача состоит в указании принадлежности входного образа, представленного вектором признаков, одному или нескольким предварительно определенным классам)
3) кластеризация (в этом случае отсутствует обучающая выборка с метками классов).
Алгоритм кластеризации основан на подобии образов и размещает похожие образы в один кластер, а не похожие – в другой.
4) прогнозирование
5) задачи оптимизации
6) задачи управления.
Для применения нейронных сетей желательно выполнение следующих условий:
1. Накоплены достаточные объемы данных о поведении системы в предыдущие периоды времени;
2. Не существует традиционных методов или алгоритмов, которые удовлетворительно решают требуемую задачу;
3. Исходные данные частично искажены, противоречивы или не полны и поэтому традиционные методы решения выдают неудовлетворительный результат.
Далее обратимся к истории развития искусственных нейронных сетей.
В модели математического нейрона можно выделить три основных элемента:
1. Набор связей (синапсов), каждая из которых характеризуется своим весом.
2. Сумматор.
3. Функция активации.
В математическом нейроне в качестве функции активации использовалась пороговая функция (рис. 3.2).
Математические нейроны могут реализовывать различные логические функции. Так, математический нейрон, имеющий два входа с единичными силами связей 
, реализует функцию логического умножения «И» при 
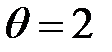и функцию логического сложения «ИЛИ» при 
.
Нейрон с одним входом, у которого 
, реализует логическую функцию «НЕТ» при 
.
Фактически рассматриваемый персептрон состоит из одного единственного математического нейрона, который вместо реализации логических функций проводит классификацию цифр на четные и нечетные.
Ограниченность однослойного персептрона
Когда Ф. Розенблатту удалось обучить персептрон распознаванию букв латинского алфавита, это был колоссальный успех.
Многослойный персептрон
Двухслойный персептрон является наиболее общим классом сетей и способен формировать произвольные выпуклые многоугольные решающие области.
Именно двухслойные персептроны, содержащие входной, скрытый и выходной слои нейронов, чаще всего применяются на практике, так как они позволяют воспроизводить достаточно сложные зависимости.
В общем случае можно выделить три фундаментальных класса архитектур нейронных сетей:
Рассмотрим чуть подробнее первый вид архитектуры.
Второй вид архитектуры –
Третий вид архитектуры –
В искусственных нейронных сетях, используемых в научных и практических целях в настоящее время используются различные функции активации. Рассмотрим наиболее распространенные из них. Пусть значение, подаваемое в качестве аргумента для пороговой функции обозначено как и ранее через 
, а выходной сигнал - 
Виды функций активации:
1. Пороговая функция 
2. Сигмоидальная функция
а) логистическая функция
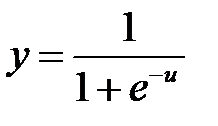
б) гиперболический тангенс
3. Линейная функция
а) с неограниченной областью изменения
б) с ограниченной областью изменения
4. Радиально-базисная функция
Рассмотрим алгоритм решения задач при использовании искуссвенных нейронных сетей:
1. Постановка задачи
2. Формирование обучающего множества (обучающей выборки)
3. Выбор нейросетевой модели (структуры нейронной сети), в рамках которой будет производиться решение задачи
4. Выполнение алгоритма обучения сети
5. Тестирование обученной сети на новых данных, которых не было в обучающем множестве.
Далее рассмотрим немного подробнее вопрос обучения нейронных сетей. В целом, суть всего процесса обучения нейросетей состоит в подстройке синаптических весов (то есть величин, обозначенных wij). Первоначальные значения указанных величин в большинстве случаев назначаются датчиком случайных чисел, после чего происходит их корректировка в соответствии с некоторыми правилами.
Схему процесса обучения нейронной сети можно представить в следующем виде:
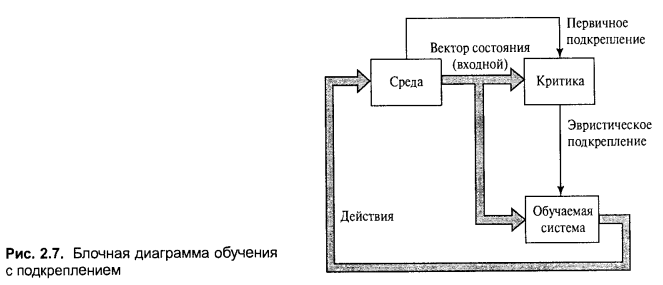
Рассмотрим парадигмы обучения нейронных сетей.
Таким образом, для обучения с учителем характерно наличие в обучающей выборке ожидаемых ответов сети. Например, для обучения нейронной сети, используемой для аппроксимации значений неизвестной функции, обучающее множество можно представить в виде:
| x | ||||||
| y | 0.6 |
Выделим наиболее распространенные алгоритмы обучения нейронных сетей в рамках обучения с учителем:
1. Методы локальной оптимизации с вычислением частных производных 1-го порядка:
а) метод градиентного спуска (наиболее распространенный пример - алгоритм обратного распространения ошибки)
б) методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента
в) метод сопряженных градиентов
2. Методы локальной оптимизации вычислением частных производных 1-го и 2-го порядков:
а) квазиньютоновские методы
б) методы оптимизации с разреженными матрицами Гессе
в) метод Левенберга-Маркардта
3. Методы стохастической оптимизации:
а) методы случайного поиска
б) метод Монте-Карло
в) метод квази Монте-Карло
4. Методы глобальной оптимизации (переборные методы).
Задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция.
Для сравнения эффективности методов обучения нейросетей используют следующие критерии:
· количество шагов алгоритма;
· количество дополнительных переменных.
Выделим наиболее распространенные алгоритмы обучения нейронных сетей в рамках обучения без учителя:
1. Алгоритмы обучения Хебба
а) сигнальный метод обучения Хебба
б) дифференциальный метод обучения Хебба
2. Алгоритм обучения Кохонена
