Имея статистические данные о результатах хозяйственной деятельности группы однородных предприятий построить пошаговым регрессионным методом многофакторную линейную регрессионную модель зависимости показателя Y (чистая прибыль предприятия, млн.грн.) от трех факторов: (основные фонды, млн.грн.), (оборотные фонды, млн.грн.), (стоимость рабочей силы, млн.грн.).
Выполнить статистический анализ (тестирование модели в целом и оценок её параметров на надежность) и содержательный (экономический) анализ оцененного уравнения регрессии.
По полученной модели сделать прогноз и оценить точность этого прогноза.
Все вычисления выполнить с использованием программы обработки электронных таблиц MS Excel.
Задание выполняется в следующей последовательности.
1.Значения исходных переменных перевести в стандартизованные значения.
2.Пошаговым регрессионным методом построить эконометрическую модель, включающую наиболее информативные факторы.
3.Пересчитать оценки параметров построенной модели в естественный масштаб и записать оцененное уравнение регрессии в естественном масштабе.
4.Полученные оценки параметров построенной модели проверить с помощью инструмента Анализа Данных «Регрессия» пакета MS Excel. Используя результаты регрессионного анализа, полученные с помощью инструмента Анализа Данных «Регрессия»:
- с надежностью 0,95 проверить статистическую значимость коэффициента детерминации (оценить адекватность принятой модели статистическим данным на основе критерия Фишера);
- если модель с заданной надежностью адекватна наблюдаемым данным, то, используя Т-тест Стьюдента, с надежностью 0,95 оценить значимость оценок параметров модели;
- построить 95%-доверительные интервалы для параметров модели;
- построить графики, отражающие характер изменения остатков регрессии.
5.Рассчитать точечную оценку прогноза показателя Y при прогнозных значениях отобранных (наиболее информативных) факторов.
Прогнозные значения отобранных факторов принять на уровне 1,15 от максимальных значений этих факторов в исходных данных.
6.С надежностью 0,95 оценить доверительный интервал для математического ожидания прогнозного значения показателя Y.
7.Выполнить экономико-математический анализ выявленной связи. Дать экономическую интерпретацию параметрам  построенной модели. По полученным результатам сделать выводы.
построенной модели. По полученным результатам сделать выводы.
Исходные данные представлены в табл.2.1-2.4.
Краткие теоретические сведения
Модель множественной регрессии
На любой исследуемый экономический показатель чаще всего оказывает влияние не один, а несколько факторов. В этом случае вместо парной регрессии рассматривается множественная регрессия.
Задача оценки статистической взаимосвязи зависимой (объясняемой, эндогенной) переменной Y и вектора (группы) независимых (объясняющих, экзогенных) переменных (факторов)  формулируется аналогично случаю парной регрессии: по имеющимся статистическим данным получить наилучшие оценки неизвестных параметров, проверить статистические гипотезы относительно параметров модели, проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).
формулируется аналогично случаю парной регрессии: по имеющимся статистическим данным получить наилучшие оценки неизвестных параметров, проверить статистические гипотезы относительно параметров модели, проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений).
Самая простая из моделей множественной регрессии – модель множественной линейной регрессии:
 , (2.1)
, (2.1)
где
 - вектор подлежащих оцениванию параметров;
- вектор подлежащих оцениванию параметров;
m - число объясняющих переменных (факторов);
 - случайная ошибка.
- случайная ошибка.
Каждый параметр  характеризует чувствительность показателя Y к изменению соответствующего фактора
характеризует чувствительность показателя Y к изменению соответствующего фактора  . Другими словами, он отражает, как в среднем влияет на объясняемую переменную Y объясняющая переменная
. Другими словами, он отражает, как в среднем влияет на объясняемую переменную Y объясняющая переменная  при условии, что все другие объясняющие переменные модели остаются постоянными.
при условии, что все другие объясняющие переменные модели остаются постоянными.
 – свободный член, определяющий значение Y в случае, когда все объясняющие переменные
– свободный член, определяющий значение Y в случае, когда все объясняющие переменные  равны нулю.
равны нулю.
После выбора линейной функции в качестве модели зависимости необходимо оценить параметры регрессии.
Таблица 2.1 – показатель Y (чистая прибыль предприятий, млн.грн.)
| Номер наблюдения | Номер варианта | ||||||||||||||
| 13,8 | 21,3 | 43,9 | 25,6 | 33,5 | 12,4 | 65,7 | 33,2 | 70,1 | 12,8 | 17,0 | 4,7 | 4,5 | 2,3 | 8,1 | |
| 8,1 | 19,6 | 41,2 | 25,2 | 41,0 | 14,9 | 71,7 | 30,5 | 71,3 | 16,6 | 21,0 | 6,2 | 5,2 | 2,9 | 8,5 | |
| 15,1 | 18,8 | 45,9 | 31,1 | 42,1 | 16,0 | 74,4 | 37,8 | 75,0 | 14,9 | 18,8 | 6,6 | 6,0 | 3,6 | 8,3 | |
| 7,5 | 19,9 | 57,5 | 33,4 | 50,4 | 15,0 | 91,1 | 40,6 | 80,1 | 20,4 | 20,7 | 6,9 | 5,6 | 3,9 | 8,8 | |
| 18,7 | 23,3 | 47,7 | 32,2 | 49,9 | 17,5 | 92,1 | 41,1 | 81,2 | 20,4 | 22,2 | 6,9 | 5,7 | 4,5 | 9,4 | |
| 22,5 | 22,1 | 59,6 | 38,8 | 50,3 | 18,3 | 93,0 | 44,1 | 85,6 | 23,2 | 20,5 | 7,4 | 6,6 | 5,0 | 9,7 | |
| 25,4 | 24,6 | 56,7 | 41,4 | 58,4 | 16,2 | 99,3 | 43,7 | 90,0 | 24,4 | 21,6 | 8,0 | 5,9 | 5,1 | 9,8 | |
| 26,8 | 25,4 | 69,1 | 47,9 | 51,4 | 17,4 | 105,3 | 52,5 | 90,5 | 25,8 | 19,6 | 9,0 | 6,2 | 5,2 | 11,3 | |
| 28,7 | 22,6 | 77,8 | 43,2 | 66,2 | 21,4 | 110,2 | 52,9 | 94,6 | 30,5 | 22,4 | 8,1 | 7,0 | 6,8 | 10,2 | |
| 31,5 | 27,9 | 81,3 | 51,6 | 65,4 | 22,6 | 115,6 | 60,6 | 95,0 | 27,6 | 20,1 | 8,4 | 6,4 | 8,0 | 10,7 | |
| 33,7 | 24,1 | 81,5 | 52,0 | 67,0 | 23,0 | 120,2 | 56,0 | 100,2 | 27,8 | 23,5 | 9,4 | 6,9 | 9,0 | 12,0 | |
| 38,6 | 26,5 | 85,6 | 54,8 | 67,2 | 24,0 | 125,0 | 57,0 | 106,8 | 27,9 | 22,7 | 9,9 | 7,4 | 9,5 | 11,8 | |
| - | 24,0 | 83,5 | 59,0 | 68,2 | 24,2 | 126,9 | 57,5 | 109,3 | 28,6 | 27,7 | 8,8 | 7,8 | 15,0 | 12,6 | |
| - | 24,5 | 82,7 | 62,1 | 68,5 | 25,0 | 130,8 | 59,6 | 112,3 | 29,0 | - | 10,2 | 8,0 | 15,5 | 13,4 | |
| - | 28,1 | 89,6 | 63,5 | 69,0 | - | 142,3 | 61,2 | 120,8 | 30,0 | - | - | 8,8 | 15,8 | 15,5 | |
| - | - | 90,1 | 67,8 | - | - | 150,2 | 62,5 | 125,7 | 30,1 | - | - | 9,3 | 16,2 | 17,7 | |
| - | - | 90,5 | 67,0 | - | - | - | - | 124,2 | 32,3 | - | - | - | 17,0 | 18,5 | |
| - | - | 87,5 | - | - | - | - | - | - | - | - | - | - | - | 19,0 | |
| - | - | 89,9 | - | - | - | - | - | - | - | - | - | - | - | 19,6 | |
| - | - | 90,1 | - | - | - | - | - | - | - | - | - | - | - | 19,5 |
Продолжение таблицы 2.1
| Номер наблюдения | Номер варианта | ||||||||||||||
| 4,2 | 16,3 | 9,1 | 54,2 | 10,9 | 41,0 | 6,4 | 53,4 | 12,0 | 99,2 | 20,8 | 7,1 | 11,9 | 62,7 | 60,6 | |
| 5,2 | 19,0 | 10,9 | 49,6 | 10,3 | 42,4 | 6,4 | 49,4 | 13,8 | 110,6 | 18,8 | 8,6 | 13,1 | 62,5 | 79,3 | |
| 7,0 | 19,6 | 12,4 | 52,3 | 9,7 | 53,6 | 7,0 | 62,1 | 14,0 | 110,7 | 25,4 | 8,0 | 14,7 | 58,9 | 45,0 | |
| 7,7 | 27,2 | 10,9 | 73,9 | 10,5 | 56,3 | 8,5 | 54,1 | 15,5 | 120,9 | 30,6 | 9,7 | 20,4 | 77,2 | 69,7 | |
| 9,1 | 29,0 | 11,5 | 67,2 | 11,1 | 51,9 | 8,3 | 54,3 | 16,6 | 135,2 | 29,5 | 9,9 | 19,4 | 67,5 | 70,4 | |
| 9,6 | 32,8 | 14,9 | 64,4 | 12,2 | 55,5 | 9,7 | 67,8 | 17,2 | 140,2 | 39,6 | 11,6 | 25,9 | 64,2 | 87,9 | |
| 10,5 | 30,2 | 15,2 | 80,0 | 10,5 | 50,4 | 11,9 | 64,9 | 17,6 | 140,6 | 46,0 | 14,2 | 29,5 | 79,9 | 88,3 | |
| 12,6 | 36,0 | 14,1 | 93,1 | 13,3 | 53,2 | 12,1 | 66,6 | 18,5 | 149,2 | 47,7 | 14,2 | 32,6 | 79,6 | 108,5 | |
| 13,2 | 41,8 | 14,5 | 95,4 | 12,3 | 63,3 | 10,9 | 67,6 | 19,1 | 155,3 | 57,4 | 16,9 | 33,7 | 73,5 | 92,5 | |
| 12,8 | 45,0 | 14,7 | 90,5 | 11,9 | 63,3 | 14,2 | 78,9 | 20,3 | 170,3 | 53,0 | 16,1 | 36,8 | 84,8 | 120,4 | |
| 13,0 | 51,2 | 18,3 | 116,1 | 11,9 | 63,7 | 15,6 | 90,1 | 21,0 | 175,2 | 60,0 | 18,8 | 35,5 | 92,0 | 130,5 | |
| 14,0 | 52,3 | 17,2 | 120,6 | 14,2 | 67,8 | 15,3 | 92,9 | 21,9 | 199,2 | 62,3 | 17,4 | 39,6 | 79,0 | 135,8 | |
| - | 55,2 | 19,4 | 125,2 | 13,3 | 64,6 | 16,9 | 95,3 | 22,5 | - | - | 19,0 | 45,6 | 97,5 | 139,9 | |
| - | 54,3 | - | 129,4 | 15,0 | 59,6 | - | 96,3 | 24,8 | - | - | 19,6 | - | 98,9 | - | |
| - | 57,6 | - | 140,8 | - | 69,2 | - | 99,1 | 25,0 | - | - | 19,0 | - | 100,1 | - | |
| - | - | - | 158,0 | - | - | - | 100,2 | - | - | - | 20,3 | - | - | - | |
| - | - | - | - | - | - | - | 105,9 | - | - | - | 22,1 | - | - | - | |
| - | - | - | - | - | - | - | 120,1 | - | - | - | 23,0 | - | - | - |
Таблица 2.2 –  (основные фонды, млн.грн.)
(основные фонды, млн.грн.)
| Номер наблюдения | Номер варианта | ||||||||||||||
| 21,4 | 3,7 | 5,5 | 4,6 | 12,8 | 3,7 | 35,5 | 15,9 | 56,2 | 12,8 | 17,5 | 25,6 | 41,8 | 50,9 | 3,0 | |
| 19,2 | 4,1 | 6,2 | 5,6 | 16,6 | 4,4 | 34,1 | 14,6 | 58,6 | 16,4 | 21,5 | 30,1 | 44,6 | 55,0 | 3,4 | |
| 19,2 | 5,0 | 7,4 | 6,2 | 14,9 | 5,2 | 30,5 | 15,3 | 60,0 | 19,4 | 25,8 | 35,5 | 42,0 | 70,1 | 3,8 | |
| 15,6 | 5,2 | 6,0 | 6,9 | 20,4 | 6,2 | 36,5 | 14,9 | 64,3 | 20,6 | 24,1 | 36,3 | 49,3 | 70,3 | 4,2 | |
| 24,4 | 5,6 | 7,1 | 6,3 | 20,4 | 7,6 | 32,1 | 18,2 | 66,2 | 22,2 | 30,0 | 51,2 | 48,6 | 75,8 | 3,9 | |
| 23,4 | 5,5 | 8,3 | 7,5 | 23,2 | 7,6 | 40,1 | 19,6 | 68,3 | 23,7 | 28,3 | 51,3 | 54,2 | 80,4 | 4,6 | |
| 21,1 | 6,5 | 8,6 | 7,0 | 24,4 | 9,3 | 34,1 | 17,2 | 69,0 | 27,2 | 36,0 | 60,5 | 62,2 | 86,3 | 4,3 | |
| 24,3 | 5,7 | 9,7 | 6,7 | 25,8 | 9,6 | 39,3 | 19,0 | 72,1 | 34,4 | 37,7 | 62,0 | 57,3 | 90,3 | 4,6 | |
| 25,4 | 7,1 | 9,2 | 8,6 | 30,5 | 11,2 | 39,2 | 21,5 | 74,3 | 34,3 | 41,2 | 68,5 | 54,1 | 100,9 | 4,5 | |
| 26,5 | 6,0 | 9,0 | 7,7 | 27,6 | 10,2 | 41,3 | 23,7 | 75,5 | 33,7 | 41,6 | 78,5 | 69,4 | 110,6 | 4,5 | |
| 25,9 | 7,6 | 8,9 | 7,7 | 27,8 | 11,2 | 40,3 | 24,0 | 74,5 | 40,2 | 45,2 | 81,3 | 60,2 | 120,3 | 5,2 | |
| 29,6 | 5,9 | 9,0 | 8,8 | 27,9 | 12,8 | 42,3 | 24,6 | 76,6 | 40,2 | 39,3 | 90,6 | 65,2 | 120,9 | 4,8 | |
| - | 6,0 | 9,4 | 9,5 | 28,6 | 12,0 | 41,5 | 24,3 | 79,8 | 41,6 | 50,0 | 98,2 | 70,1 | 125,9 | 5,3 | |
| - | 6,8 | 9,5 | 10,6 | 29,0 | 13,3 | 43,6 | 26,3 | 77,7 | 43,3 | - | 105,6 | 75,5 | 140,6 | 4,9 | |
| - | 7,0 | 8,9 | 10,9 | 29,7 | - | 45,0 | 26,0 | 80,2 | 42,1 | - | - | 74,9 | 150,3 | 5,0 | |
| - | - | 9,6 | 11,3 | - | - | 44,8 | 27,0 | 79,2 | 45,4 | - | - | 72,3 | 164,2 | 5,2 | |
| - | - | 9,9 | 11,1 | - | - | - | - | 81,2 | 44,3 | - | - | - | 169,2 | 5,3 | |
| - | - | 10,9 | - | - | - | - | - | - | - | - | - | - | - | 5,9 | |
| - | - | 11,9 | - | - | - | - | - | - | - | - | - | - | - | 5,7 | |
| - | - | 12,0 | - | - | - | - | - | - | - | - | - | - | 5,7 |
Продолжение таблицы 2.2
| Номер наблюдения | Номер варианта | ||||||||||||||
| 20,5 | 4,5 | 9,0 | 4,4 | 26,9 | 9,2 | 9,5 | 8,8 | 4,9 | 12,8 | 2,7 | 19,5 | 10,4 | 27,9 | 2,8 | |
| 21,1 | 5,5 | 8,0 | 5,0 | 32,0 | 10,4 | 12,0 | 8,6 | 6,2 | 16,9 | 3,8 | 24,0 | 11,3 | 29,7 | 2,9 | |
| 27,7 | 6,7 | 9,7 | 6,9 | 30,0 | 13,7 | 11,3 | 10,0 | 5,7 | 18,6 | 5,7 | 23,9 | 11,0 | 30,2 | 4,4 | |
| 25,2 | 8,9 | 11,3 | 7,4 | 35,8 | 13,2 | 14,9 | 9,6 | 5,9 | 18,9 | 7,4 | 26,7 | 12,5 | 30,5 | 4,3 | |
| 30,9 | 9,2 | 11,0 | 7,4 | 35,2 | 15,6 | 15,7 | 10,9 | 7,0 | 25,4 | 7,0 | 31,2 | 12,7 | 29,8 | 5,1 | |
| 26,8 | 10,6 | 13,2 | 8,3 | 44,1 | 13,7 | 17,8 | 11,1 | 5,1 | 29,1 | 7,6 | 37,4 | 13,7 | 39,3 | 5,7 | |
| 34,5 | 10,9 | 14,0 | 8,9 | 51,2 | 18,1 | 18,9 | 11,8 | 6,1 | 29,6 | 11,7 | 39,3 | 13,7 | 34,7 | 5,8 | |
| 35,3 | 11,1 | 12,8 | 12,1 | 53,0 | 17,5 | 20,1 | 10,8 | 6,9 | 27,8 | 11,6 | 41,1 | 13,8 | 33,6 | 7,9 | |
| 35,1 | 14,4 | 14,1 | 14,8 | 54,4 | 18,0 | 18,3 | 12,1 | 6,7 | 30,6 | 11,6 | 42,6 | 12,6 | 42,2 | 7,9 | |
| 40,3 | 15,4 | 14,7 | 15,1 | 60,5 | 21,4 | 19,2 | 12,9 | 7,8 | 40,7 | 14,1 | 48,2 | 12,0 | 37,8 | 7,4 | |
| 40,0 | 16,2 | 15,4 | 14,2 | 55,4 | 21,6 | 20,0 | 11,2 | 8,0 | 44,5 | 16,2 | 43,2 | 13,5 | 42,5 | 8,1 | |
| 40,3 | 17,0 | 15,7 | 16,3 | 59,8 | 21,0 | 23,0 | 13,7 | 8,2 | 47,6 | 15,3 | 42,9 | 14,6 | 36,9 | 9,0 | |
| - | 18,0 | 17,5 | 15,9 | 66,0 | 24,3 | 27,1 | 12,6 | 9,0 | - | - | 43,8 | 14,8 | 42,0 | 9,3 | |
| - | 18,3 | - | 17,3 | 72,5 | 24,3 | - | 15,2 | 8,9 | - | - | 45,6 | - | 45,8 | - | |
| - | 19,0 | - | 18,5 | - | 27,0 | - | 15,7 | 9,5 | - | - | 47,9 | - | 45,9 | - | |
| - | - | - | 20,1 | - | - | - | 16,3 | - | - | - | 47,3 | - | - | - | |
| - | - | - | - | - | - | - | 14,3 | - | - | - | 49,2 | - | - | - | |
| - | - | - | - | - | - | - | 17,0 | - | - | - | 50,0 | - | - | - |
Таблица 2.3 –  (оборотные фонды, млн.грн.)
(оборотные фонды, млн.грн.)
| Номер наблюдения | Номер варианта | ||||||||||||||
| 16,4 | 10,6 | 14,1 | 11,9 | 12,8 | 22,8 | 6,6 | 3,5 | 1,9 | 2,5 | 1,0 | 50,2 | 7,2 | 25,3 | 27,4 | |
| 7,7 | 11,7 | 11,4 | 13,3 | 16,4 | 23,4 | 6,4 | 4,1 | 2,4 | 3,6 | 1,1 | 59,6 | 9,2 | 30,6 | 29,1 | |
| 11,6 | 13,7 | 14,0 | 12,8 | 19,4 | 26,9 | 7,4 | 5,0 | 2,5 | 4,3 | 1,4 | 70,6 | 11,6 | 32,5 | 32,0 | |
| 9,7 | 11,1 | 14,4 | 14,6 | 20,6 | 32,6 | 6,7 | 6,3 | 2,6 | 4,8 | 1,5 | 85,3 | 13,4 | 36,2 | 29,1 | |
| 15,5 | 13,3 | 17,7 | 14,5 | 22,2 | 33,5 | 7,3 | 6,2 | 2,6 | 5,5 | 1,8 | 92,3 | 13,4 | 38,0 | 34,5 | |
| 17,3 | 12,3 | 16,1 | 17,0 | 23,7 | 38,6 | 9,3 | 7,8 | 2,9 | 5,1 | 2,1 | 100,3 | 14,8 | 40,2 | 37,1 | |
| 19,7 | 13,3 | 18,5 | 15,5 | 27,2 | 40,1 | 9,8 | 9,1 | 2,9 | 5,3 | 2,3 | 115,6 | 15,4 | 41,6 | 34,7 | |
| 21,8 | 12,8 | 21,8 | 15,3 | 34,4 | 45,7 | 8,7 | 8,5 | 3,1 | 5,2 | 2,5 | 119,6 | 15,8 | 48,3 | 35,6 | |
| 19,5 | 14,4 | 20,5 | 15,8 | 34,3 | 53,5 | 8,4 | 9,9 | 3,3 | 5,5 | 3,2 | 140,3 | 16,2 | 50,5 | 43,4 | |
| 22,5 | 14,4 | 23,8 | 18,0 | 33,7 | 49,8 | 9,3 | 9,6 | 3,0 | 5,7 | 3,4 | 150,3 | 16,5 | 52,6 | 43,7 | |
| 21,5 | 13,2 | 22,6 | 17,1 | 40,2 | 50,3 | 9,5 | 12,8 | 3,3 | 6,1 | 3,5 | 160,2 | 17,0 | 59,3 | 41,4 | |
| 20,7 | 16,0 | 24,0 | 20,4 | 40,2 | 53,6 | 9,5 | 11,6 | 3,4 | 7,3 | 4,2 | 165,2 | 17,1 | 60,0 | 49,1 | |
| - | 16,1 | 24,2 | 19,1 | 41,6 | 52,1 | 9,9 | 11,6 | 3,2 | 6,0 | 4,4 | 172,3 | 18,0 | 65,3 | 44,9 | |
| - | 15,8 | 25,0 | 19,9 | 43,3 | 55,2 | 10,1 | 13,0 | 3,6 | 7,5 | - | 180,1 | 18,5 | 68,3 | 47,1 | |
| - | 15,6 | 29,0 | 21,4 | 42,1 | - | 11,0 | 12,4 | 3,6 | 9,3 | - | - | 19,2 | 70,1 | 47,8 | |
| - | - | 27,7 | 21,7 | - | - | 11,8 | 13,7 | 3,7 | 8,6 | - | - | 20,5 | 75,2 | 48,7 | |
| - | - | 29,0 | 22,6 | - | - | - | - | 4,0 | 9,0 | - | - | - | 78,4 | 48,3 | |
| - | - | 26,6 | - | - | - | - | - | - | - | - | - | - | - | 50,3 | |
| - | - | 31,1 | - | - | - | - | - | - | - | - | - | - | - | 51,3 | |
| - | - | 32,5 | - | - | - | - | - | - | - | - | - | - | - | 54,3 |
Продолжение таблицы 2.3
| Номер наблюдения | Номер варианта | ||||||||||||||
| 8,5 | 19,4 | 10,1 | 11,9 | 16,6 | 4,3 | 7,4 | 15,0 | 60,5 | 23,3 | 5,7 | 14,2 | 2,4 | 10,1 | 4,8 | |
| 9,6 | 23,6 | 12,7 | 11,0 | 15,8 | 4,5 | 9,3 | 15,2 | 65,8 | 25,6 | 6,4 | 15,6 | 3,0 | 11,1 | 5,6 | |
| 8,6 | 27,4 | 11,8 | 11,5 | 17,7 | 5,2 | 9,0 | 16,7 | 69,6 | 30,4 | 9,1 | 14,5 | 3,9 | 12,3 | 5,5 | |
| 9,9 | 29,1 | 14,9 | 15,6 | 20,4 | 5,2 | 9,6 | 14,3 | 75,1 | 32,8 | 9,0 | 16,7 | 5,1 | 15,2 | 8,1 | |
| 11,5 | 29,4 | 15,3 | 15,7 | 23,8 | 5,7 | 11,1 | 17,8 | 82,0 | 36,6 | 9,1 | 15,5 | 5,4 | 15,8 | 6,9 | |
| 11,7 | 34,1 | 16,6 | 17,4 | 24,5 | 6,5 | 9,8 | 18,1 | 84,2 | 46,9 | 12,1 | 16,6 | 5,5 | 17,2 | 8,8 | |
| 11,3 | 34,2 | 16,4 | 15,7 | 26,6 | 6,4 | 11,6 | 15,9 | 89,3 | 47,8 | 14,5 | 19,3 | 6,9 | 18,1 | 8,5 | |
| 12,5 | 39,1 | 17,9 | 19,9 | 29,0 | 7,4 | 13,5 | 20,0 | 95,1 | 49,8 | 15,1 | 19,2 | 7,7 | 19,2 | 8,1 | |
| 13,2 | 35,6 | 19,6 | 16,5 | 31,9 | 8,3 | 14,0 | 21,4 | 95,6 | 54,4 | 15,6 | 18,4 | 7,4 | 19,8 | 9,0 | |
| 12,8 | 39,0 | 18,6 | 21,5 | 31,3 | 7,9 | 11,5 | 21,3 | 101,2 | 55,2 | 15,5 | 23,7 | 9,5 | 20,2 | 12,1 | |
| 13,1 | 42,1 | 18,9 | 17,9 | 33,9 | 8,9 | 14,5 | 25,1 | 110,5 | 71,2 | 19,6 | 20,7 | 10,6 | 21,1 | 14,0 | |
| 14,0 | 44,3 | 21,2 | 20,3 | 35,1 | 10,7 | 15,4 | 22,0 | 105,6 | 69,0 | 21,5 | 24,2 | 10,9 | 22,6 | 16,0 | |
| - | 45,9 | 21,8 | 21,1 | 32,9 | 9,1 | 14,4 | 26,3 | 112,5 | - | - | 23,3 | 9,9 | 25,4 | 14,6 | |
| - | 48,3 | - | 23,0 | 38,1 | 11,2 | - | 27,8 | 120,9 | - | - | 25,1 | - | 28,1 | - | |
| - | 47,5 | - | 24,0 | - | 10,2 | - | 28,3 | 131,8 | - | - | 27,0 | - | 29,5 | - | |
| - | - | - | 22,2 | - | - | - | 27,1 | - | - | - | 27,5 | - | - | - | |
| - | - | - | - | - | - | - | 29,1 | - | - | - | 28,1 | - | - | - | |
| - | - | - | - | - | - | - | 31,6 | - | - | - | 27,9 | - | - | - |
Таблица 2.4 –  (стоимость рабочей силы, млн.грн.)
(стоимость рабочей силы, млн.грн.)
| Номер наблюдения | Номер варианта | ||||||||||||||
| 12,0 | 31,3 | - | 29,1 | - | 5,8 | - | 33,3 | - | 4,2 | 35,0 | - | 35,5 | - | - | |
| 11,5 | 27,4 | - | 29,2 | - | 6,5 | - | 43,2 | - | 7,0 | 39,2 | - | 34,4 | - | - | |
| 10,9 | 35,9 | - | 33,3 | - | 7,2 | - | 41,1 | - | 7,8 | 40,1 | - | 30,5 | - | - | |
| 10,6 | 29,4 | - | 30,8 | - | 6,5 | - | 40,7 | - | 8,2 | 48,1 | - | 36,5 | - | - | |
| 9,5 | 38,7 | - | 32,8 | - | 7,4 | - | 49,3 | - | 10,0 | 48,5 | - | 32,1 | - | - | |
| 10,0 | 35,4 | - | 37,1 | - | 7,9 | - | 56,1 | - | 10,6 | 55,2 | - | 40,1 | - | - | |
| 9,0 | 36,3 | - | 30,8 | - | 8,1 | - | 57,6 | - | 9,6 | 50,9 | - | 34,1 | - | - | |
| 8,4 | 36,4 | - | 33,4 | - | 7,7 | - | 51,1 | - | 10,1 | 56,0 | - | 39,3 | - | - | |
| 7,9 | 42,9 | - | 35,5 | - | 7,9 | - | 60,7 | - | 10,8 | 67,2 | - | 39,2 | - | - | |
| 7,5 | 40,6 | - | 34,8 | - | 10,2 | - | 62,0 | - | 12,4 | 61,2 | - | 41,1 | - | - | |
| 7,1 | 47,7 | - | 39,2 | - | 9,7 | - | 57,2 | - | 12,0 | 60,7 | - | 42,5 | - | - | |
| 6,6 | 50,7 | - | 41,4 | - | 10,3 | - | 59,4 | - | 13,4 | 75,4 | - | 45,2 | - | - | |
| - | 49,8 | - | 45,4 | - | 11,3 | - | 60,2 | - | 13,6 | 68,9 | - | 45,8 | - | - | |
| - | 50,0 | - | 40,9 | - | 12,3 | - | 61,3 | - | 14,4 | - | - | 43,9 | - | - | |
| - | 48,9 | - | 40,4 | - | - | - | 63,4 | - | 14,6 | - | - | 50,5 | - | - | |
| - | - | - | 42,6 | - | - | - | 64,0 | - | 15,0 | - | - | 48,3 | - | - | |
| - | - | - | 43,9 | - | - | - | - | - | 16,3 | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Продолжение таблицы 2.4
| Номер наблюдения | Номер варианта | ||||||||||||||
| 32,7 | 6,0 | 12,3 | - | - | 36,4 | 54,0 | - | - | 10,2 | - | - | 41,1 | 25,0 | - | |
| 32,1 | 6,1 | 11,5 | - | - | 42,5 | 57,7 | - | - | 10,9 | - | - | 41,5 | 28,8 | - | |
| 34,2 | 7,2 | 11,5 | - | - | 52,3 | 49,8 | - | - | 11,0 | - | - | 39,8 | 31,8 | - | |
| 40,4 | 7,8 | 11,6 | - | - | 61,2 | 56,0 | - | - | 12,5 | - | - | 50,2 | 37,0 | - | |
| 38,7 | 9,9 | 14,0 | - | - | 66,5 | 54,9 | - | - | 13,1 | - | - | 42,6 | 39,7 | - | |
| 42,8 | 11,7 | 11,8 | - | - | 56,6 | 59,0 | - | - | 13,5 | - | - | 46,3 | 43,8 | - | |
| 46,3 | 12,8 | 13,7 | - | - | 85,4 | 73,8 | - | - | 13,8 | - | - | 55,6 | 45,0 | - | |
| 45,5 | 12,8 | 13,4 | - | - | 82,9 | 66,4 | - | - | 15,2 | - | - | 53,6 | 48,6 | - | |
| 47,9 | 14,8 | 14,0 | - | - | 86,6 | 67,4 | - | - | 16,6 | - | - | 48,6 | 49,1 | - | |
| 39,9 | 15,7 | 16,3 | - | - | 89,6 | 63,7 | - | - | 16,9 | - | - | 48,9 | 50,2 | - | |
| 48,1 | 15,6 | 16,7 | - | - | 97,7 | 68,5 | - | - | 17,9 | - | - | 58,3 | 52,9 | - | |
| 47,3 | 16,3 | 14,4 | - | - | 82,6 | 74,7 | - | - | 19,0 | - | - | 51,1 | 56,5 | - | |
| - | 17,6 | 18,2 | - | - | 89,1 | 88,5 | - | - | - | - | - | 64,6 | 63,2 | - | |
| - | 17,3 | - | - | - | 106,4 | - | - | - | - | - | - | - | 70,1 | - | |
| - | 18,0 | - | - | - | 111,1 | - | - | - | - | - | - | - | 73,9 | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| - | - | - | - | - | - | - | - | - | - | - | - | - | - |
Как и в случае парной регрессии, истинные значения параметров по выборке получить невозможно. В этом случае оценивается уравнение регрессии:
 , (2.2)
, (2.2)
где
 - оценка показателя Y;
- оценка показателя Y;
 - оценки истинных значений параметров
- оценки истинных значений параметров  в естественном (размерном) масштабе.
в естественном (размерном) масштабе.
Самым распространенным методом оценки параметров уравнения множественной линейной регрессии является обычный метод наименьших квадратов (МНК).
При этом следует иметь ввиду, что сравнивать силу влияния отдельных факторов на величину результирующего показателя Y, сопоставляя значения параметров в естественном масштабе по их величине, нельзя, так как параметры в естественном масштабе зависят от единиц измерения каждого фактора.
С целью выявления наиболее влияющих факторов необходимо перейти к уравнению в стандартизованном масштабе, в котором в качестве единицы измерения влияния всех факторов выступает их среднее квадратичное отклонение.
Метод оценки параметров множественной линейной регрессии в стандартизованном масштабе
При построении уравнения регрессии в стандартизованном масштабе все значения переменных переводятся в стандартизованные значения. Для этого значения исходных переменных центрируют (т.е. смещают на величину их среднего по выборке значения) и нормируют (путем деления значений центрированных переменных на соответствующие среднеквадратические отклонения исходных переменных в выборке) по формулам:
 ;
;  ,
,  ,…,
,…,  , (2.3)
, (2.3)
где
 - стандартизованная объясняемая переменная;
- стандартизованная объясняемая переменная;
 - среднее по выборке значение объясняемой переменной
- среднее по выборке значение объясняемой переменной  ;
;
 - стандартизованные объясняющие переменные;
- стандартизованные объясняющие переменные;
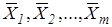 - средние по выборке значения объясняющих переменных
- средние по выборке значения объясняющих переменных  ,
,  ;
;
 - среднеквадратические отклонения показателя Y и факторов
- среднеквадратические отклонения показателя Y и факторов  , которые вычисляются по формулам:
, которые вычисляются по формулам:
 ;
;  , (2.4)
, (2.4)
где n – число рассматриваемых наблюдений.
Таким образом, начало отсчета каждой






