Характерной чертой адаптивных методов прогнозирования является их способность непрерывно учитывать эволюцию динамических характеристик изучаемых процессов, «адаптироваться» к этой эволюции, придавая тем больший вес, тем более высокую информационную ценность имеющимся наблюдениям, чем ближе они к текущему моменту прогнозирования.
В основе процедуры адаптации лежит метод проб и ошибок. По модели делается прогноз на один интервал по времени. Через один шаг моделирования анализируется результат: насколько он далек от фактического значения. Затем в соответствии с моделью происходит корректировка. После этого процесс повторяется. Таким образом, адаптация осуществляется рекуррентно с получением каждой новой фактической точки ряда.
Методы экспоненциального сглаживания. Модель Брауна.
Пусть анализируемый временной ряд x(t) представлен в виде:
x(t) = a0 + ε(t),
где a0 – неизвестный параметр, не зависящий от времени, ε(t) - случайный остаток со средним значением, равным нулю, и конечной дисперсией.
В соответствии с методом Брауна прогноз x*(t+τ) для неизвестного значения x(t+τ) по известной до момента времени t траектории ряда x(t) строится по формуле:
x*(t; τ) = S(t),
где значение экспоненциально взвешенной скользящей средней S (t) определяется по рекуррентной формуле:
S(t) = αx(t) + (1-α) S(t-1).
Коэффициент сглаживания α можно интерпретировать как коэффициент дисконтирования, характеризующий меру обесценивания информации за единицу времени. Из формулы следует, что экспоненциально взвешенная скользящая средняя является взвешенной суммой всех уровней ряда x(t), причем веса уменьшаются экспоненциально по мере удаления в прошлое.
В качестве S (0) берется, как правило, среднее значение ряда динамики или среднее значение нескольких начальных уровней ряда.
Случай линейного тренда: x(t) = a0 + a1t + ε(t).
В этом случае прогноз x*(t; τ) будущего значения определяется соотношением:
x*(t; τ) =  ,
,
а пересчет коэффициентов  осуществляется по формулам:
осуществляется по формулам:

Начальные значения коэффициентов берутся из оценки тренда линейной функцией.
Модель Хольта.
В модели Хольта введено два параметра сглаживания α 1 и α 2 (0< α 1, α 2 <1). Прогноз x*(t;l) на l шагов по времени определяется формулой:
x*(t; τ) =  ,
,
а пересчет коэффициентов  осуществляется по формулам:
осуществляется по формулам:

Модель Хольта-Уинтерса.
Эта модель помимо линейного тренда учитывает и сезонную составляющую. Прогноз x*(t;τ) на τ шагов по времени определяется формулой:
x*(t;τ) =  ,
,
где f(t) – коэффициент сезонности, а T – число временных тактов (фаз), содержащихся в полном сезонном цикле.
Видно, что в данной модели сезонность представлена мультипликативно. Формулы обновления коэффициентов имеют вид:

Модель Тейла-Вейджа.
Если исследуемый временной ряд имеет экспоненциальную тенденцию с мульти-пликативной сезонностью, то после логарифмирования обеих частей уравнения получается модель с линейной тенденцией и аддитивной сезонностью или модель Тейла-Вейджа.
Имеется модель:
x(t) = a0(t) + g(t) + δ(t),
a0(t) = a0(t-1) + a1(t).
Здесь a0(t) – уровень процесса после устранения сезонных колебаний, a1(t) – аддитивный коэффициент роста, ω(t) – аддитивный коэффициент сезонности и δ(t) – белый шум.
Прогноз x*(t;τ) на τ шагов по времени определяется формулой:
x*(t;τ) =  .
.
Коэффициенты вычисляются рекуррентным способом по формулам:

Для определения оптимальных значений параметров адаптации перебирают различные наборы их значений и сравнивают получающиеся при этом среднеквадратические ошибки прогнозов.
Задача 1.
В табл. 1 приведены данные о личных потребительских расходах и располагаемом личном доходе населения США (млрд. дол., в ценах 1972 г.) за период с 1959 г. по 1983 г.
а) Постройте уравнение для функции спроса (Y) на данный товар или вид услуг в зависимости от располагаемого личного дохода (X). Постройте таблицу дисперсионного анализа. Вычислите коэффициент детерминации R 2.
Проверьте регрессию на значимость с помощью F -теста (α = 0,05 - критерий значимости). Вычислите 95% доверительные интервалы для истинных значений коэффициентов в этом уравнении. Изобразите диаграмму рассеяния и прямую регрессии.
б) Постройте линейный временной тренд для функции спроса.
в) Рассмотрите функцию спроса (Y) как функцию двух переменных: располагаемого дохода (X) и реальной цены на товар или вид услуг (P). (Реальная цена вычисляется по формуле
P = (Z / L) ∙ 100%). (Z, L см. табл. 1).
Постройте уравнение множественной регрессии Y на X и P. С помощью МНК оцените коэффициенты в этом уравнении (замените Y, X и P на их логарифмы).
Дайте экономическую интерпретацию коэффициентов в уравнении. Вычислите коэффициенты эластичности функции спроса. Интерпретируйте эти коэффициенты.
Таблица 1
Исходные данные о личных потребительских расходах и располагаемом личном доходе
| Год | Личный располагаемый доход, млрд. $ | Текущие расходы на бензин | Дефляторы цен для личных потребительских расходов | Цены |
| T | X | Y | Z | L |
| 440,4 | 13,7 | 82,2 | 70,6 | |
| 452,0 | 14,2 | 84,5 | 71,9 | |
| 461,4 | 14,3 | 83,9 | 72,6 | |
| 482,0 | 14,9 | 84,5 | 73,7 | |
| 500,5 | 15,3 | 84,5 | 74,8 | |
| 528,0 | 16,0 | 84,4 | 75,9 | |
| 557,5 | 16,8 | 87,5 | 77,2 | |
| 646,8 | 17,8 | 89,5 | 79,4 | |
| 673,5 | 18,4 | 92,4 | 81,4 | |
| 701,3 | 19,9 | 93,8 | 84,6 | |
| 722,5 | 21,4 | 97,0 | 88,4 | |
| 751,6 | 22,9 | 97,9 | 92,5 | |
| 779,2 | 24,2 | 98,7 | 96,3 | |
| 810,3 | 25,4 | 109,0 | 100,0 | |
| 865,3 | 26,2 | 109,4 | 105,7 | |
| 858,4 | 24,8 | 147,7 | 116,3 | |
| 875,8 | 25,6 | 157,7 | 125,2 | |
| 906,8 | 26,8 | 164,3 | 131,7 | |
| 942,9 | 27,7 | 173,7 | 139,3 | |
| 988,8 | 28,3 | 181,3 | 149,1 | |
| 1015,5 | 27,4 | 243,2 | 162,5 | |
| 1021,6 | 25,1 | 337,9 | 179,0 | |
| 1049,3 | 25,1 | 376,4 | 194,3 | |
| 1058,3 | 25,3 | 356,6 | 206,0 | |
| 1095,4 | 26,1 | 344,9 | 213,6 |
Решение
а) Постройте уравнение для функции спроса (Y) на данный товар или вид услуг в зависимости от располагаемого личного дохода (X). Постройте таблицу дисперсионного анализа. Вычислите коэффициент детерминации R 2.
Проверьте регрессию на значимость с помощью F -теста (α = 0,05 - критерий значимости). Вычислите 95% доверительные интервалы для истинных значений коэффициентов в этом уравнении. Изобразите диаграмму рассеяния и прямую регрессии.
Идентифицируем переменные: x - независимая переменная (фактор) y - зависимая переменная (показатель).
Пусть эконометрическая модель специфицирована в линейной форме:
y = ax + b + u
где a, b - параметры модели u - стохастическая составляющая (остатки).
Используем метод наименьших квадратов [ЛЕЩ, с.29].
Запишем систему нормальных уравнений, используя в качестве неизвестной переменной - переменную x:

где n - количество наблюдений.
Построим вспомогательную таблицу 1.
Табл. 1.
| № | x | y | x 2 | xy |
| 440,4 | 13,7 | 193952,16 | 6033,48 | |
| 452,0 | 14,2 | 204304,00 | 6418,40 | |
| 461,4 | 14,3 | 212889,96 | 6598,02 | |
| 482,0 | 14,9 | 232324,00 | 7181,80 | |
| 500,5 | 15,3 | 250500,25 | 7657,65 | |
| 528,0 | 16,0 | 278784,00 | 8448,00 | |
| 557,5 | 16,8 | 310806,25 | 9366,00 | |
| 646,8 | 17,8 | 418350,24 | 11513,04 | |
| 673,5 | 18,4 | 453602,25 | 12392,40 | |
| 701,3 | 19,9 | 491821,69 | 13955,87 | |
| 722,5 | 21,4 | 522006,25 | 15461,50 | |
| 751,6 | 22,9 | 564902,56 | 17211,64 | |
| 779,2 | 24,2 | 607152,64 | 18856,64 | |
| 810,3 | 25,4 | 656586,09 | 20581,62 | |
| 865,3 | 26,2 | 748744,09 | 22670,86 | |
| 858,4 | 24,8 | 736850,56 | 21288,32 | |
| 875,8 | 25,6 | 767025,64 | 22420,48 | |
| 906,8 | 26,8 | 822286,24 | 24302,24 | |
| 942,9 | 27,7 | 889060,41 | 26118,33 | |
| 988,8 | 28,3 | 977725,44 | 27983,04 | |
| 1015,5 | 27,4 | 1031240,25 | 27824,70 | |
| 1021,6 | 25,1 | 1043666,56 | 25642,16 | |
| 1049,3 | 25,1 | 1101030,49 | 26337,43 | |
| 1058,3 | 25,3 | 1119998,89 | 26774,99 | |
| 1095,4 | 26,1 | 1199901,16 | 28589,94 | |
| Σ | 19185,1 | 543,6 | 15835512,07 | 441628,55 |
Получим систему уравнений:
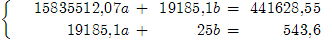
Решение системы найдем по формулам Крамера [ГЕТ, с.30]:

где Δ - главный определитель системы.

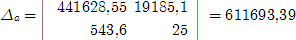



Следовательно, уравнение линейной модели имеет вид:
y = 4,8705 + 0,0220 x.
Это значит, что при увеличении или уменьшении значения фактора на 1 у.е. показатель увеличивается или уменьшается на 0,022 у.е., то есть между эконометрическими параметрами существует прямая пропорциональная или положительная зависимость.
Свободный член регрессии b = 4,8705 указывает значение показателя при нулевом значении фактора. Он имеет лишь расчетное значение, поскольку такой случай невозможен в реальной экономической ситуации.
Для проведения исследования модели построим вспомогательную таблицу 2.
Табл. 2.
| № | x | y | yx | 
| 
| 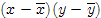
| 
| u 2 = (y - yx)2 |
| 440,4 | 13,7 | 14,5539 | 64,7059 | 106931,6160 | 2630,4202 | 51,6973 | 0,7292 | |
| 452,0 | 14,2 | 14,8090 | 56,9119 | 99479,6832 | 2379,4078 | 48,0945 | 0,3709 | |
| 461,4 | 14,3 | 15,0157 | 55,4131 | 93638,4480 | 2277,8938 | 45,2705 | 0,5122 | |
| 482,0 | 14,9 | 15,4686 | 46,8403 | 81455,4432 | 1953,3050 | 39,3805 | 0,3233 | |
| 500,5 | 15,3 | 15,8754 | 41,5251 | 71237,7452 | 1719,9294 | 34,4407 | 0,3311 | |
| 528,0 | 16,0 | 16,4800 | 32,9935 | 57314,2752 | 1375,1366 | 27,7092 | 0,2304 | |
| 557,5 | 16,8 | 17,1287 | 24,4431 | 44059,6892 | 1037,7654 | 21,3011 | 0,1080 | |
| 646,8 | 17,8 | 19,0922 | 15,5551 | 14545,3248 | 475,6622 | 7,0321 | 1,6698 | |
| 673,5 | 18,4 | 19,6793 | 11,1823 | 8817,9612 | 314,0150 | 4,2631 | 1,6365 | |
| 701,3 | 19,9 | 20,2905 | 3,4003 | 4369,7388 | 121,8958 | 2,1126 | 0,1525 | |
| 722,5 | 21,4 | 20,7567 | 0,1183 | 2016,3692 | 15,4470 | 0,9748 | 0,4139 | |
| 751,6 | 22,9 | 21,3965 | 1,3363 | 249,7664 | -18,2694 | 0,1208 | 2,2605 | |
| 779,2 | 24,2 | 22,0034 | 6,0319 | 139,1456 | 28,9710 | 0,0673 | 4,8252 | |
| 810,3 | 25,4 | 22,6872 | 13,3663 | 1840,0668 | 156,8278 | 0,8896 | 7,3594 | |
| 865,3 | 26,2 | 23,8965 | 19,8559 | 9583,6268 | 436,2246 | 4,6333 | 5,3061 | |
| 858,4 | 24,8 | 23,7448 | 9,3391 | 8280,2720 | 278,0838 | 4,0032 | 1,1135 | |
| 875,8 | 25,6 | 24,1274 | 14,8687 | 11749,6928 | 417,9750 | 5,6805 | 2,1686 | |
| 906,8 | 26,8 | 24,8090 | 25,5631 | 19431,2448 | 704,7862 | 9,3942 | 3,9641 | |
| 942,9 | 27,7 | 25,6028 | 35,4739 | 30798,8460 | 1045,2542 | 14,8900 | 4,3984 | |
| 988,8 | 28,3 | 26,6120 | 42,9811 | 49016,1888 | 1451,4722 | 23,6974 | 2,8493 | |
| 1015,5 | 27,4 | 27,1991 | 31,9903 | 61551,6252 | 1403,2310 | 29,7578 | 0,0404 | |
| 1021,6 | 25,1 | 27,3332 | 11,2627 | 64615,6064 | 853,0818 | 31,2391 | 4,9872 | |
| 1049,3 | 25,1 | 27,9423 | 11,2627 | 79465,3548 | 946,0430 | 38,4184 | 8,0784 | |
| 1058,3 | 25,3 | 28,1401 | 12,6451 | 84620,4828 | 1034,4262 | 40,9107 | 8,0664 | |
| 1095,4 | 26,1 | 28,9559 | 18,9747 | 107581,3760 | 1428,7506 | 52,0114 | 8,1561 | |
| Σ | 19185,1 | 543,6 | - | 608,0416 | 1112789,5896 | 24467,7356 | 537,9904 | 70,0512 |
| Σ/ n | 767,404 | 21,744 | - | 24,3217 | 44511,5836 | 978,7094 | 21,5196 | 2,8020 |
Оценим параметры модели альтернативным способом:

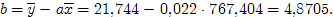
Линейное уравнение регрессии аналогично: yx = 0,022 x + 4,8705.
Вычислим для зависимой переменной y общую дисперсию, дисперсию, что объясняет регрессию, дисперсию ошибок [ЛУК, с. 56]:




Суммы квадратов связанные с определенным источником вариации, а также со степенями свободы и средними квадратами. Сведем их всех в таблице, которая называется базовой таблицей дисперсионного анализа - ANOVA-таблицей [ЛУК, с. 61].
Построим ANOVA-таблицу о зависимости между показателем и фактором:
| Источник вариации | Количество степеней свободы | Сумма квадратов | Средние квадраты |
| Предопределено регрессией (модель) | 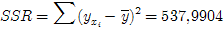
| 
| |
| Необъяснимо с помощью регрессии (ошибки) | n - 2 = 23 | 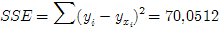
| 
|
| Общее | n - 1 = 24 | 
| - |
Определим коэффициенты детерминации R 2 и корреляции r [ЛУК, c. 57]:

Этот результат значит, что 88,48% вариации результативного признака зависит от вариации уровня факторного признака, а 11,52% приходится на другие факторы.

Поскольку 0,7 < r < 1, то между факторным и результативным признаком корреляционная связь сильная.
Проверим адекватность модели по критерию Фишера или F -критерию,
который вычисляется по формуле:

Поскольку табличное значение F (0,05; 1; 23) = 4,28 и | F | > Fтаб, то делаем вывод об адекватности эконометрической модели.
Оценим статистическую значимость параметров регрессии.
Табличное значение t -критерия Стьюдента при заданном уровне значимости 0,95 и n - 2 = 23 степенях свободы равно 2,07.
Найдем матрицу погрешностей C -1, обратную к матрице системы уравнений:

Δ = | C | = 27819739,74,

Определим стандартные погрешности оценок параметров модели, учитывая дисперсию остатков:


где 
Рассчитаем t -критерий Стьюдента для каждого из коэффициентов


Поскольку tm = 2,07 и это значение больше t -критериев для каждого из коэффициентов, то делаем вывод об их статистической значимости.
Определим интервалы доверия для параметров регрессии [ЕЛИ, с. 57].
Для расчета доверительного интервала определяем предельную погрешность для каждого коэффициента:
Δ a = tтаб.ma = 2,0690 · 0,0017 = 0,0034,
Δ b = tтаб.mb = 2,0690 · 1,3167 = 2,7242,
Следовательно, экстремальные значения для каждого коэффициента следующие:
min a = a - Δ a = 0,0220 - 0,0034 = 0,0186, max a = a + Δ a = 0,0220 + 0,0034 = 0,0254,
min b = b - Δ b = 4,8705 - 2,7242 = 2,1463, max b = b + Δ b = 4,8705 + 2,7242 = 7,5947.
Таким образом, доверительные интервалы для коэффициентов регрессии следующие:
a Î (0,0186; 0,0254),
b Î (2,1463; 7,5947).
Изобразим диаграмму рассеяния и прямую регрессии.
б) Постройте линейный временной тренд для функции спроса.
Идентифицируем переменные: t - независимая временная переменная (фактор), y - зависимая переменная (показатель). Пусть модель специфицирована в линейной форме:
y = at + b + u,
где a, b - параметры модели, u - стохастическая составляющая (остатки).
Используем метод наименьших квадратов [ЛЕЩ, с.29].
Запишем систему нормальных уравнений, используя в качестве неизвестную переменную - переменную t:

Расчет параметров значительно упрощается, если за начало счета времени (t = 0) принять центральный интервал (момент).
При нечетном числе уровней (например, 25), значения t = 0 – условного обозначения времени будет отвечать среднему 1971 году:
| t | -12 | -11 | -10 | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | |
| Y | 13,7 | 14,2 | 14,3 | 14,9 | 15,3 | 16,8 | 17,8 | 18,4 | 19,9 | 21,4 | 22,9 | 24,2 | |
| t | |||||||||||||
| Y | 25,4 | 26,2 | 24,8 | 25,6 | 26,8 | 27,7 | 28,3 | 27,4 | 25,1 | 25,1 | 25,3 | 26,1 |
Поскольку Σ t = 0, поэтому система нормальных уравнений принимает вид:

Построим вспомогательную таблицу:
| № | t | y | t 2 | ty |
| -12 | 13,7 | -164,4 | ||
| -11 | 14,2 | -156,2 | ||
| -10 | 14,3 | -143,0 | ||
| -9 | 14,9 | -134,1 | ||
| -8 | 15,3 | -122,4 | ||
| -7 | 16,0 | -112,0 | ||
| -6 | 16,8 | -100,8 | ||
| -5 | 17,8 | -89,0 | ||
| -4 | 18,4 | -73,6 | ||
| -3 | 19,9 | -59,7 | ||
| -2 | 21,4 | -42,8 | ||
| -1 | 22,9 | -22,9 | ||
| 24,2 | 0,0 | |||
| 25,4 | 25,4 | |||
| 26,2 | 52,4 | |||
| 24,8 | 74,4 | |||
| 25,6 | 102,4 | |||
| 26,8 | 134,0 | |||
| 27,7 | 166,2 | |||
| 28,3 | 198,1 | |||
| 27,4 | 219,2 | |||
| 25,1 | 225,9 | |||
| 25,1 | 251,0 | |||
| 25,3 | 278,3 | |||
| 26,1 | 313,2 | |||
| Σ | - | 543,6 | 819,6 |
Получим систему уравнений:

Находим решение:
a = 819,6 / 1300 = 0,6305,
b = 543,6 / 25 = 21,744.
Следовательно, уравнение линейного тренда имеет вид:
y = 21,7440 + 0,6305 t.
Это значит, что при увеличении или уменьшении значения временного фактора на 1 ед., показатель увеличивается или уменьшается на 0,6305 у.е., то есть между параметрами существует прямая пропорциональная или положительная зависимость.
Свободный член регрессии b = 21,744 указывает значение показателя при нулевом значении условного времени.
в) Рассмотрите функцию спроса (Y) как функцию двух переменных: располагаемого дохода (X) и реальной цены на товар или вид услуг (P). (Реальная цена вычисляется по формуле
P = (Z / L) ∙ 100%). (Z, L см. табл. 1).
Постройте уравнение множественной регрессии Y на X и P. С помощью МНК оцените коэффициенты в этом уравнении (замените Y, X и P на их логарифмы).
Дайте экономическую интерпретацию коэффициентов в уравнении. Вычислите коэффициенты эластичности функции спроса. Интерпретируйте эти коэффициенты.
Искомое уравнение множественной регрессии выражается производственной функцией или функцией Кобба-Дугласа [НАК, c.140]:
Y = c Xa Pb,
где c - коэффициент, что отображает уровень технологической производительности, показатели a и b - коэффициенты элластичности объема производства Y по фактору производства, то есть по капиталу X и реальной цене P соответственно.
Для оценки параметров производственной регрессии сведем ее к линейной форме. После логарифмирования и замены величин получим приведенную линейную регрессию:
lg Y = lg(c Xa Pb),
lg Y = lg c + a lg X + b lg P.
Обозначим:
lg Y = y, lg c = a 0, a = a 1, b = a 2, lg X = x 1, lg P = x 2,
где X - количество фактора 1, P - количество фактора 2, Y - показатель.
Получили эконометрическую модель, которая специфицирована в линейной форме:
y = a 0 + a 1 x 1 + a 2 x 2 + u,
где a 0, a 1, a 2 - параметры модели u - стохастическая составляющая (остатки).
Запишем исходные данные в такой форме.
| № | Y | X | P |
| 13,7 | 440,4 | 116,43 | |
| 14,2 | 117,52 | ||
| 14,3 | 461,4 | 115,56 | |
| 14,9 | 114,65 | ||
| 15,3 | 500,5 | 112,97 | |
| 16,0 | 111,2 | ||
| 16,8 | 557,5 | 113,34 | |
| 17,8 | 646,8 | 112,72 | |
| 18,4 | 673,5 | 113,51 | |
| 19,9 | 701,3 | 110,87 | |
| 21,4 | 722,5 | 109,73 | |
| 22,9 | 751,6 | 105,84 | |
| 24,2 | 779,2 | 102,49 | |
| 25,4 | 810,3 | ||
| 26,2 | 865,3 | 103,5 | |
| 24,8 | 858,4 | ||
| 25,6 | 875,8 | 125,96 | |
| 26,8 | 906,8 | 124,75 | |
| 27,7 | 942,9 | 124,69 | |
| 28,3 | 988,8 | 1215,96 | |
| 27,4 | 1015,5 | 149,66 | |
| 25,1 | 1021,6 | 188,77 | |
| 25,1 | 1049,3 | 193,72 | |
| 25,3 | 1058,3 | 173,11 | |
| 26,1 | 1095,4 | 161,47 |
После логарифмирования получим исходные данные для расчетов.
| № | y | x 1 | x 2 | № | y | x 1 | x 2 | |
| 1,1367 | 2,6438 | 2,0661 | 1,4048 | 2,9086 | 2,0374 | |||
| 1,1523 | 2,6551 | 2,0701 | 1,4183 | 2,9372 | 2,0149 | |||
| 1,1553 | 2,6641 | 2,0628 | 1,3945 | 2,9337 | 2,1038 | |||
| 1,1732 | 2,6830 | 2,0594 | 1,4082 | 2,9424 | 2,1002 | |||
| 1,1847 | 2,6994 | 2,0530 | 1,4281 | 2,9575 | 2,0960 | |||
| 1,2041 | 2,7226 | 2,0461 | 1,4425 | 2,9745 | 2,0958 | |||
| 1,2253 | 2,7462 | 2,0544 | 1,4518 | 2,9951 | 3,0849 | |||
| 1,2504 | 2,8108 | 2,0520 | 1,4378 | 3,0067 | 2,1751 | |||
| 1,2648 | 2,8283 | 2,0550 | 1,3997 | 3,0093 | 2,2759 | |||
| 1,2989 | 2,8459 | 2,0448 | 1,3997 | 3,0209 | 2,2872 | |||
| 1,3304 | 2,8588 | 2,0403 | 1,4031 | 3,0246 | 2,2383 | |||
| 1,3598 | 2,8760 | 2,0246 | 1,4166 | 3,0396 | 2,2081 | |||
| 1,3838 | 2,8916 | 2,0107 |
Построим модель множественной линейной регрессии.
Пусть эконометрическая модель специфицирована в линейной форме [ЛЕЩ, c. 58]:
Y = a 0 + a 1 X 1 + a 2 X 2 + u,
где a 0, a 1, a 2 - параметры модели u - стохастическая составляющая (остатки), X 1, X 2 - факторы Y - показатель. Оценим параметры модели методом МНК:
A = (X ' X)-1 X ' Y,
где матрица X характеризует все независимые переменные модели. Поскольку модель имеет свободный член a 0, для которого все xi = 1, то матрицу нужно дополнить первым столбцом, в котором все члены являются единицами, X ' - транспонированная матрица к данной, а вектор Y - вектор зависимой переменной.

Транспонируем данную матрицу:

Найдем произведение транспонированной матрицы и данной:

Вычислим обратную матрицу:

Найдем произведение транспонированной матрицы и вектора Y:

Умножив обратную матрицу на предыдущую, получим искомые коэффициенты:

Таким образом a 0 = -0,9638, a 1 = 0,8074, a 2 = -0,0122.
Следовательно, линейная эконометрическая модель имеет вид:
Y = -0,9638 + 0,8074 X 1 - 0,0122 X 2.
Проверку правильности решения можно выполнить, использовав стандартную функцию Excel ЛИНЕЙН() [ЛАВ, c. 249]. Задав первым ее параметром значения диапазона Y, а вторым - диапазона X, получим аналогичный результат.
С экономической точки зрения вычисленные коэффициенты регрессии значат следующее:
- если значение фактора x 1 () изменится на 1, то показатель увеличится или уменьшится на 0,8074 ед.;
- если значение фактора x 2 () изменится на 1, то показатель увеличится или уменьшится на 0,0122 ед.;
Свободный член регрессии a 0 = -0,9638 указывает значение результативного признака при нулевых значениях всех факторов. Он имеет лишь расчетное значение, поскольку такой случай невозможный в реальной экономической ситуации.
Коэффициент c функции Кобба-Дугласа определяем потенцированием:
c = ea o = e -0,9638 = 0,1087
a = a 1 = 0,8074
b = a 2 = -0,0122
Следовательно, функция Кобба-Дугласа следующая:
Y = 0,1087· X 0,8074· P -0,0122.
Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью коэффициентов частной эластичности, которые в случае данной двуфакторной модели они равны вычисленным коэффициентам a = 0,8074 и b = -0,0122.
Коэффициенты частной эластичности показывают, на сколько процентов изменится результативный признак, если значение одной из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.
Задача 2.
Объем продаж рекламного времени частной радиостанции за 21 неделю представлен в табл. 2. Проанализировать кривую объемов продаж рекламного времени и сделать вывод о возможности повышения прибыльности этого вида деятельности.
При решении этой задачи необходимо выполнить следующие операции:
1) проанализировать ряд количества проданного рекламного времени и построить его график;
2) выбрать общую статистическую модель;
3) оценить трендовую составляющую Ui;
4) оценить адекватность построенных моделей тренда и оценить их точность;
5) осуществить прогноз объемов продаж рекламного времени на следующие 4 недели.
В задаче необходимо применить три аппроксимирующих, полинома (линейный, параболический и гиперболический), провести их сравнение и выбор наилучшего.
Таблица 2
Исходные данные об объеме продаж рекламного времени
| Число недель | Количество проданного времени, мин. |
Решение
Проанализируем ряд количества проданного рекламного времени и построим для наглядности диаграмму рассеивания или график ряда.
Проанализировав размещение точек, приходим к выводу о хаотичности их размещения в первой половине рассмативаемых недель. Во второй половине точки находятся уже ближе к некоторой прямой линии, свидетельствующей об уменьшении количества проданного рекламного времени.
Для возможности построения адекватных економико-математических моделей и определения тенденции продаж увеличим интервал от одной недели до трех и вычислим скользящие средние, то есть выполним сглаживание ряда с помощью трехчленной скользящей:
| Число недель | Количество проданного, времени, мин. | ||
| Одна неделя | Сумма 3 недель | Среднее 3 недель | |
| – | – | ||
| 178,00 | |||
| 236,67 | |||
| 326,00 | |||
| 303,67 | |||
| 208,00 | |||
| 166,33 | |||
| 215,33 | |||
| 247,67 | |||
| 250,33 | |||
| 218,00 | |||
| 236,67 | |||
| 218,33 | |||
| 295,67 | |||
| 295,33 | |||
| 292,33 | |||
| 230,67 | |||
| 229,00 | |||
| 218,67 | |||
| 206,00 | |||
| – | – |
Построим диаграмму сглаженного ряда.
Как и предполагалось, разброс точек значительно уменьшился.
Таким образом, получен рабочий набор данных для проведения анализа продаж рекламного времени.
Построим линейный, параболический и гиперболический тренд и в дальнейшем определим лучший из них.
Линейная модель
Пусть модель специфицирована в линейной форме:
y = at + b + u,
где a, b - параметры модели, u - стохастическая составляющая (остатки).
Используем метод наименьших квадратов.
Запишем систему нормальных уравнений, используя в качестве неизвестную переменную - переменную t:

Расчет параметров значительно упрощается, если за начало счета времени (t = 0) принять центральный интервал (момент).
При нечетном числе уровней (например, 19), значения t = 0 – условного обозначения времени будет отвечать средней 11 неделе:
| t | -9 | -8 | -7 | -6 | -5 | -4 | -3 | -2 | -1 | |
| Y | 178,00 | 236,67 | 326,00 | 303,67 | 208,00 | 166,33 | 215,33 | 247,67 | 250,33 | 218,00 |
| t | |||||||||
| Y | 236,67 | 218,33 | 295,67 | 295,33 | 292,33 | 230,67 | 229,00 | 218,67 | 206,00 |
Поскольку Σ t = 0, поэтому система нормальных уравнений принимает вид:

Построим вспомогательную таблицу:
| № | t | y | t 2 | ty |
| -9 | 178,00 | -1602,00 | ||
| -8 | 236,67 | -1893,36 | ||
| -7 | 326,00 | -2282,00 | ||
| -6 | 303,67 | -1822,02 | ||
| -5 | 208,00 | -1040,00 | ||
| -4 | 166,33 | -665,32 | ||
| -3 | 215,33 | -645,99 | ||
| -2 | 247,67 | -495,34 | ||
| -1 | 250,33 | -250,33 | ||
| 218,00 | 0,00 | |||
| 236,67 | 236,67 | |||
| 218,33 | 436,66 | |||
| 295,67 | 887,01 | |||
| 295,33 | 1181,32 | |||
| 292,33 | 1461,65 | |||
| 230,67 | 1384,02 | |||
| 229,00 | 1603,00 | |||
| 218,67 | 1749,36 | |||
| 206,00 | 1854,00 | |||
| Σ | - | 4572,67 | 97,33 |
Получим систему уравнений:
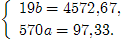
Находим решение:
a = 97,33 / 570 = 0,1708,
b = 4572,67 / 19 = 240,6668.
Следовательно, уравнение линейного тренда имеет вид:
y = 240,6668 + 0,1708 t.
Это значит, что при увеличении или уменьшении значения фактора на 1 у.е., показатель увеличивается или уменьшается на 0,1708 у.е., то есть между параметрами существует прямая пропорциональная или положительная зависимость.
Свободный член регрессии b = 240,6668 указывает значение показателя при нулевом значении условного времени.
Вычислим теоретические значения уровней ряда динамики по аналитической формуле и трендовую составляющую Ui.
| № | t | T | y | p | Ui |
| -9 | 178,00 | 239,1301 | -61,1301 | ||
| -8 | 236,67 | 239,3008 | -2,6308 | ||
| -7 | 326,00 | 239,4716 | 86,5284 | ||
| -6 | 303,67 | 239,6423 | 64,0277 | ||
| -5 | 208,00 | 239,8131 | -31,8131 | ||
| -4 | 166,33 | 239,9838 | -73,6538 | ||
| -3 | 215,33 | 240,1546 | -24,8246 | ||
| -2 | 247,67 | 240,3253 | 7,3447 | ||
| -1 | 250,33 | 240,4961 | 9,8339 | ||
| 218,00 | 240,6668 | -22,6668 | |||
| 236,67 | 240,8376 | -4,1676 | |||
| 218,33 | 241,0084 | -22,6784 | |||
| 295,67 | 241,1791 | 54,4909 | |||
| 295,33 | 241,3499 | 53,9801 | |||
| 292,33 | 241,5206 | 50,8094 | |||
| 230,67 | 241,6914 | -11,0214 | |||
| 229,00 | 241,8621 | -12,8621 | |||
| 218,67 | 242,0329 | -23,3629 | |||
| 206,00 | 242,2036 | -36,2036 |
Выполним построение корреляционного поля с изображением на нем тренда.
Вычислим для зависимой переменной y общую дисперсию, дисперсию, что объясняет регрессию, дисперсию ошибок [ЛУК, с. 56]:


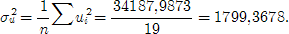
Определим коэффициенты детерминации R 2 и корреляции r [ЛУК, c. 57]:

Этот результат значит, что 0,05% вариации результативного признака зависит от вариации уровня факторного признака, а 99,95% приходится на другие факторы.

Поскольку | r | < 0,4, то между факторным и результативным признаком корреляционной связи нет.
Оценим точность модели или среднюю ошибку аппроксимации как среднюю арифметическую простую по формуле [ЕЛИ, с. 87]:

Получим:

Поскольку A > 7%, то делаем вывод о плохом подборе модели для исходных данных.
Проверим адекватность модели по критерию Фишера или F -критерию,
который вычисляется по формуле:

Поскольку табличное значение F (0,05; 1; 17) = 4,45 и | F | < Fтаб, то делаем вывод об неадекватности эконометрической модели.
Методом математической экстраполяции составим прогноз показателя на следующие 4 недели.
Y (22) = 240,6668 + 0,1708 · 11 = 242,5451,
Y (23) = 240,6668 + 0,1708 · 12 = 242,7159,
Y (24) = 240,6668 + 0,1708 · 13 = 242,8866,
Y (25) = 240,6668 + 0,1708 · 14 = 243,0574.
Гиперболическая модель
Пусть эконометрическая модель специфицирована в нелинейной, гиперболической форме:
y = a 0 + a 1 / x + u.
где a, b - параметры модели u - стохастическая составляющая (остатки).
Для оценки параметров нелинейной регрессии сведем ее к линейной форме, то есть линеаризуем ее [ЕЛИ, с. 62]. Преобразуем начальное уравнение, записав его следующим образом:
y = a 0 + a 1 / x.
Произведя замену X = 1 / x, b = a 0, a = a 1, получим линейную эконометрическую модель:
y = b + aX.
Запишем исходные данные в форме, учитывая на замену.
| № | x | y | 1/ x | |
| 178,00 | 0,5000 | |||
| 236,67 | 0,3333 | |||
| 326,00 | 0,2500 | |||
| 303,67 | 0,2000 | |||
| 208,00 | 0,1667 | |||
| 166,33 | 0,1429 | |||
| 215,33 | 0,1250 | |||
| 247,67 | 0,1111 | |||
| 250,33 | 0,1000 | |||
| 218,00 | 0,0909 | |||
| 236,67 | 0,0833 | |||
|
|
|
|
|
|
Дата добавления: 2017-02-24; Мы поможем в написании ваших работ!; просмотров: 812 | Нарушение авторских прав
Лучшие изречения:
Ген: 0.011 с.






