1. Импортирование 3D-модели в пакет гидродинамического моделирования STARCCM+. Модель представляет из себя область течения. Контрольный клапан показан в практически закрытом положении. Поток входит в ближайший конец геометрии и выходит из дальнего конца геометрии. Будет использована только половина геометрии по причине ее симметричности.
2. Определение типов граничных условий: 5 поверхностей, разделенных по углу (45 градусов);
3. Настройка параметров расчетной сетки и ее построение:
Для основной сетки:
| Параметр сетки | Свойство | Величина |
| Базовый размер | Значение | 0.06 м |
| Толщина призматических слоев > Относительный размер | Процент от базы | 4.0 |
| Размер на поверхности>Относительный минимальный размер | Процент от базы | 4.0 |
| Размер на поверхности>Относительный желаемый размер | Процент от базы | 8.0 |
Для области стенки рядом с клапаном создаются дополнительные ячейки:
| Параметр сетки | Свойство | Величина |
| Базовый размер | Значение | 0.06 м |
| Толщина призматических слоев > Относительный размер | Процент от базы | 2.0 |
| Размер на поверхности > Относительный минимальный размер | Процент от базы | 4.0 |
| Размер на поверхности>Относительный желаемый размер | Процент от базы | 4.0 |
4. Задание физической модели (стационарный режим, жидкость, турбулентный режим течения, разделенное течение, решатель – разделенный; постоянная плотность, k-omega SST модель турбулентности);
5. Определение граничных условий (на выходе задается давление 0 Па; на входе задается скорость течения – 0.1; 1 и 3 м/с для 3 различных расчетов);
6. Создание мониторов и отчетов;
7. Создание визуализации отчета;
8. Запуск расчета;
9. Анализ результатов расчета.
1)Расчет при значении V=0.1 м/с
Рис 1. Распределение скоростей
Рис. 2 Полный напор
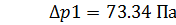
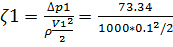=14.67
2)Расчет при значении V=1 м/с
Рис 3. Распределение скоростей
Рис. 4 Полный напор
=10.47
3)Расчет при значении V=3 м/с
Рис 5. Распределение скоростей
Рис. 6 Полный напор
=10.77
Рис. 7 Коэффициент сопротивления
Вывод:
Коэффициент местного сопротивления самый высокий при самой низкой скорости (v=0.1 м/с) на входе. График показывает, что коэффициент местного сопротивления зависит от числа Рейнольдса; график напоминает гиперболу.
Контрольные вопросы
1. Зачем отдельно настраивать параметры расчетной сетки для границ дросселирующего зазора?
Зазор между внешней стенкой и клапаном очень узкий, и для его расчета требуется повысить точность. Поэтому мы задаем очень мелкую сетку.
2. Чем отличается система уравнений, описывающих ламинарный режим течения от системы уравнений k-w модели турбулентности?
В системе уравнений k-w модели турбулентности появляются:
А) уравнение переноса кинетической энергии турбулентности;
Б) уравнение переноса относительной скорости диссипации турбулентности;
В) уравнение для нахождения Рейнольдсовых напряжений, полученное из гипотезы Буссенеска.
3. От какого безразмерного комплекса зависит коэффициент сопротивления дросселирующего зазора?
Коэффициент сопротивления дросселирующего зазора зависит от числа Рейнольдса. Re= V*d/ν
4. От чего зависит коэффициент местного сопротивления клапана при неизменной его проточной части?
Из формулы видно, что коэффициент местного сопротивления клапана зависит от разницы давлений, плотности и скорости.
