Механикалық толқындар. Механикалық не серпімді толқындар деп серпімді ортада таралатын механикалық қозуларды (деформациялар) атайды. Ортаға әсер ете отырып, осы қозуларды тудырушы денелер толқындардың көзі деп аталады.
Дыбыстық не акустикалық толқындар деп интенсивтілігі аз серпімді толқындарды, яғни серпімді ортада таралатын әлсіз механикалық қозуларды атайды.
Серпімді толқындардың ортада таралуы заттың орнын ауыстырумен байланыста емес. Шексіз ортада ол орта бөлектері толқын көздерінен барған сайын алыстай беретін жағдайда оларды мәжбүрлі тербелістерге тартудан тұрады. Мұнда орта құрылымы толық орта ретінде қарастырылады.
Егер орта бөлшектері толқынның таралу бағытында тербелетін болса, серпімді толқын бойлық деп аталады,. Бойлық толқындар серпімді ортаның көлемді деформациясымен байланысты, сондықтан кез кеген ортада – қатты, сұйық, газ тәрізді – тарала алады. Мұндай толқындардың мысалы ретінде ауадағы дыбыс толқындарын айтуға болады.
Серпімді деформация. Форманың серпімділігі. Көлемдік серпімділік.
Серпімді толқын көлденең деп аталады, егер, орта бөлшегі толқынның таралу бағытына перпендикуляр жазықтықтарда тербелсе. Көлденең толқындар серпімді ортаның ығысу деформациясымен байланысты, демек, тек формасы серпімді ортада ғана, яғни қатты денелерде пайда болып, тарала алады.
Ерекше орынды сұйықтың еркін беті бойымен таралатын беттік толқындар алады, бұл беттін қозуы сыртқы әсердің күшімен туындайды.
Серпімді толқын синусоидалды, немесе гармониялы делінеді, егер тиісінше, орта бөлшектерінің тербелістері гармониялы болса. Бұл тербелестердің жиілігі толқынның жиілігі деп аталады.
Ортаның жекелеген бөліктерінің ортаны бойлай, қайсыбір белгілі жылдамдықпен таралушы гармониялық қозғалысы гармониялық қума толқын деп аталады.
Механикалық қозулар (деформациялар) серпімді ортада v шекті жылдамдығымен таралады.
Сұйықтардағы молекулалық құбылыстар. Молекулалық қысым. Беттік керілу. Капиллярлық құбылыстар. Ерітінділер. Осмостық қысым.
Сұйық молекуласына айналысындағы басқа молекулалар тарапынан тартылу күштері әсер етеді. Егер молекула сұйық бетінен молекулалық әсерлесу сферасының радиусынан артық арақашықтықта, демек, сұйық ішіндегі орналасса, онда оған әсер етуші күштер тепе теңдік күйде болады. егер молекула қалыңдығы молекулалақы әсерлесу сферасының радиусына тең болатын шекаралық қабатта болса, онда оған сұйық ішіне қарай бағытталған қорытқы күш әсер етеді. Сондықтан молекуланы сұйық ішінен беттік қабатқа шығару үшін жұмыс атқару керек. Сұйық бетінің ауданын изотермиялық және квазистатикалық бір бірлікке (көлемді сақтап) арттыруға қажетті жұмысты сұйықтың беттік керілуі деп атайды. Изотермиялық жұмыс жүйенің еркін энергиясының кемуіне тең. Сыртқы күштер әсер етпейтін сұйықтың еркін энергиясын мына түрде жазуға болады:
(1)
Мұндағы 
еркін энергияның көлемдік және беттік құраушылары. Егер сұйықтың көлемі өте үлкен болса, онда 
, демек 
. Ал, егер сұйықтың көлемі аз болса, онда 
. Жоғарыда айтылғандарды ескерсек
(2)
мұндағы 
сұйықтың беттік керілуі, 
сұйық бетінің ауданы. Сонымен беттік керілуді сұйық аудан бірлігіндегі беттің еркін энергиясы ретінде қарастыруға болады.
2.Тік бұрышты сымнан жасалған каркас алайық. Каркастың СД бөлігі АС және ВД бағыттары бойынша еркін сырғи алсын.АВДС ауданына жұқа сабын қабыршақ тартайық. Бұл қабыршақ екі жақты. Осы екі қабыршақтың ортасында сұйық бар. Тәжірибелерден қабырщақтың қысқаруға ұмтылатынын көруге болады. сондықтан СД жоғары қарай қозғалады. СД-ны орнында ұстап тұру үшін белгілі күшпен әсер ету керек, мысалы жүк ілу керек. Қабықша екеу болғандықтан бұл күшті 2Ғ деп белгілейміз. Егер температураны тұрақты етіп ұстап Ғ күшін өте аз шамаға көбейтсек, онда СД төмен қарай 
жол жүреді және қабыршақ үстінен 
жұмыс атқарады. Бұл кезде қабыршақ ауданы 
шамаға артады. Мұндағы l- СД ның ұзындығы; 
әрбір қабықшаның ауданының өсімшесі. 
. Осы екі өрнекті теңестіріп,
(3)
екенін анықтаймыз.
(4)
Бұдан қабықшаның керілген күйде екенін көруге болады.
Сұйықтың беттік керілуін анықтағанда оның қандай ортамен шектесетінін білу қажет. Беттік керілу температура артқанда кемиді
(5)
Қамыс қанты ерітіндісінің әртүрлі концентрациясының осмостық қысымдарын зерттеп, Пфеффер менде Фриз алған нәтижелерін пайдалана отырып 1887 жылы Ван-Гофф осмостық қысым заңдылықтарын ашты. Ол күшті сұйытылған ерітіндінің осмостық қысымы идеал газ заңдарына бағытталумен анықталады. Тұрақты температурада осмостық қысым концентрацияға тура пропорционал, еріген заттың массалық көлеміне кері пропорционал екендігімен анықталады.
Р1 /Р2 = С1 /С2
Егер концентрция тұрақты болса, осмостық қысым термодинамикалық температурасын тап.
Р1 /Р =T1 / T2
Бірдей температура мен бірдей концентрацияда әр түрлі заттардың бірдей осмостық қысымдары болады.Осы заңдылықтарды біріктіргенде осмостық қысымға арналған күй теңдеуін аламыз.
P = m/v·RT = CRT (Вант-Гофф теңдеуі)
Бұл формула бойынша клайпейрон – Менделеев теңдеуіне тура келеді.
c=m/v – молярлық концентрация.
R – универсал газ тұрақтысы, Т- термодинамикалық температура, С – концентрация төмен болған сайын Вант-Гофф теңдеуі орындалмайды. Концентрация жоғары болған сайын Вант-Гофф теңдеуінен ауытқулар болады.Жоғары концентрациялар кезінде вант-Гофф заңынан ауытқуларды ескеруге болады, егерде көлемдік молярлық концентрацияның орнына молялдық концентрацияны Сm қолданса болады.
P = CmRT = RT m1 / m2M· 1000
m1 – еріген зат массасы, m2 – ерітіндінің массасы. Вант-Гоффтың біріктірілген ерітіндінің осмостық қысымы еріген зат газ күйінде сол температураларды ерітіндінің көлеміндегі көлемде түсіретін газ қысымына тең болады. Сондықтан нағыз ерітіндідегі осмостық қысым үшін еріген бөлшектердің массасы, өлшемдері пішінін емес,тек бөлшектер санының ғана маңызы болады. Осмостық жануарлар мен өсімдіктердің тіршілік әрекетіндегі маңызы зор. Ол өсімдік сабағымен судың көтерілуін клетканың өсуін т.б. құбылыстарды қамтамасыз етеді. Бірдей жағдайда бірдей осмостық қысымдары болатын ерітінділер изотондық ерітінділер деп аталады.
Клетка сыртындағы ерітіндінің осмостық қысымы клетка ішінен жоғары болса гипертондық ерітінділер, ал төмен болса гипотондық ерітінділер делінеді. Адам қанының осмостық қысымы 0,8 мПа. Мұндай осмостық қысым 0,9 0/0 NaCI ерітіндісінде де болады. Сондықтан мұндай концентрациялы ерітіндіні физиологиялық ерітінділер деп аталады.
Потенциалдар айырымы. Электр қозғаушы күш. Кернеу. Джоуль-Ленц заңының интрегралды және дифференциалды көрінісі, оны қорытып шығару.
Тізбек бөлігіндегі кернеу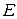 
дегеніміз электростатикалық өрістің қорытқы күші мен осы тізбек бөлігінде бірлік зарядты орын ауыстыруға жұмсалатын сыртқы күштердің жұмыстарының қосындысына тең физикалық шама.
Неміс физигі Ом тәжірибе жүзінде біртекті метал өткізгіштен өтетін ток күші өткізгіш ұштарындағы кернеуге тура пропорциональ екендігін дәлелдеді:
Өткізгіш кедергісі оның өлшеміне, формасына және материалына байланысты. Цилиндрлік өткізгіштің кедергісі 
оның ұзындығы 
-ге тура, ал көлденең қимасының ауданы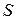 
-ке кері пропорциональ болады: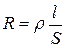 
мұндағы 
- пропорциональдық коэффициент, ол өткізгіш материалына байланысты. Ол меншікті электрлік кедергі деп аталады.
Ом заңын дифференциаль түрде жазып көрсетуге болады.
Бұл өткізгіштің әрбір нүктесіндегі ток тығыздығын осы нүктедегі электростатикалық өріс кернеулігімен байланыстыратын дифференциаль түрдегі Ом заңы.
Өткізгіштерді тізбектей қосқанда олардың кедергілері қосылады 
, ал параллель қосқанда кедергіге кері шамалары қосылады: 
Тәжірибелер көрсеткендей кедергінің температураға сызықты тәуелді.
мұндағы және 
, және 
- 
және 
температуралардағы сәйкесінше өткізгіштің меншікті кедергісі мен кедергісі. 
- кедергінің температуралық коэффициенті, ол таза металдар үшін 
.
Біртекті өткізгіштің ұштарына 
кернеу берілсін. Осы өткізгіштің көлденең қимасы арқылы 
уақыт ішінде 
заряд тасымалданады. Сонда токтың жұмысы 
Егер өткізгіш кедергісі болса, онда Ом заңын қолдана отырып былай жазуға болады: 
Токтың қуаты 
- бұл теңдеу тұрақты ток үшін де, айнымалы ток үшін де қолданылады.
Егер ток қозғалмайтын металл өткізгіштен өтетін болса, онда токтың барлық жұмысы осы өткізгішті қыздыруға кетеді де, энергияның сақталу заңы бойынша 
- Джоуль-Ленц заңының теңдеуі.
Өткізгіштен элементар цилиндрлік көлем 
бөліп алайық. Оның кедергісі 
. Джоуль-Ленц заңы бойынша уақыт ішінде осы көлемнің бөліп шығаратын жылуы 
Бірлік уақытта, бірлік көлемнен бөлініп шығатын жылу мөлшері токтын меншікті жылулық қуаты деп аталады. Ол мынаған тең: 
Ом заңының дифференциаль формасын және 
қатынасын қолдана отырып, аламыз 
бұл теңдеу Джоуль-Ленц заңының дифференциаль формасы. Оны тұрақты және айнымалы токқа және кез келген өткізгішке қолдануға болады. Егер берілген тізбек бөлігінде ток көзі болмаса (
), онда 
Егер электр тізбегі тұйық болса, онда 
; 
мұндағы 
-тізбектегі э.қ.к., ал - тізбектің толық кедергісі. Жалпы түрде 
, 
- ток көзінің ішкі кедергісі, 
- сыртқы бөлік кедергісі. Сондықтан берілген тізбекке арналған Ом заңы мына түрде болады: 
. Егер тізбек тұйық болмаса, онда ток жоқ, ендеше Ом заңына сәйкес 
.
Үштен кем емес өткізгіштердің қиылысқан нүктесін түйін деп атайды. Түйінге кіретін токтар оң, ал түйіннен шығатын токтар теріс деп есептеледі.
Кирхгофтың І-ші ережесі: түйіндегі токтардың алгебралық қосындысы нольге тең:
Кирхгофтың ІІ-ші заңы:Тармақталған электр тізбегінің кез келген тұйық контурындағы ток күші мен кедергінің көбейтіндісінің алгебралық қосындысы осы контурда кездесетін э.қ.к. алгебралық қосындысына тең.
