Основными характеристиками системы массового обслуживания любого вида являются:
1. Входной поток требований. Для описания входного потока требуется задать вероятностный закон, определяющий последовательность моментов поступления требований на обслуживание, и указать количество таких требований в каждом очередном поступлении.
При этом, как правило, оперируют понятием «вероятностное распределение моментов поступления требований». Здесь могут поступать как единичные, так и групповые требования (количество таких требований в каждом очередном поступлении). В последнем случае обычно речь идет о системе обслуживания с параллельно-групповым обслуживанием.
Пусть:
Аi – время поступления между требованиями – независимые одинаково распределенные случайные величины;
E(A) – среднее (МО) время поступления;
λ=1/E(A) – интенсивность поступления требований;
Характеристики входного потока:
Вероятностный закон, определяющий последовательность моментов поступления требований на обслуживание.
Количество требований в каждом очередном поступлении для групповых потоков.
2. Дисциплина очереди
Очередь – совокупность требований, ожидающих обслуживания.
Очередь имеет имя.
Дисциплина очереди определяет принцип, в соответствии с которым поступающие на вход обслуживающей системы требования подключаются из очереди к процедуре обслуживания. Чаще всего используются дисциплины очереди, определяемые следующими правилами:
1. Первым пришел – первый обслуживаешься; - амый распространенный тип очереди.
Какая структура данных подойдет для описания такой очереди? Массив плох (ограничен). Можно использовать структуру типа СПИСОК.
Список имеет начало и конец. Список состоит из записей. Запись – это ячейка списка. Заявка поступает в конец списка, а выбирается на обслуживание из начала списка. Запись состоит из характеристики заявки и ссылки (указатель, за кем стоит). Кроме этого, если очередь с ограничением на время ожидания, то еще должно быть указано предельное время ожидания.
Вы как программисты должны уметь делать списки двусторонние, односторонние.
Действия со списком:
вставить в хвост; взять из начала; удалить из списка по истечении времени ожидания.
2. Пришел последним — обслуживаешься первым LIFO (обойма для патронов, тупик на железнодорожной станции, зашел в набитый вагон).
3. Структура, известная как СТЕК. Может быть описан структурой массив или список;
случайный отбор заявок; отбор заявок по критерию приоритетности.
Каждая заявка характеризуется помимо прочего уровнем приоритета и при поступлении помещается не в хвост очереди, а в конец своей приоритетной группы. Диспетчер осуществляет сортировку по приоритету.
Характеристики очереди
ограничение времени ожидания момента наступления обслуживания (имеет место очередь с ограниченным временем ожидания обслуживания, что ассоциируется с понятием «допустимая длина очереди»);
длина очереди.
Механизм обслуживания
Механизм обслуживания определяется характеристиками самой процедуры обслуживания и структурой обслуживающей системы. К характеристикам процедуры обслуживания относятся:
1. количество каналов обслуживания (N);
2. продолжительность процедуры обслуживания (вероятностное распределение времени обслуживания требований);
3. количество требований, удовлетворяемых в результате выполнения каждой такой процедуры (для групповых заявок);
4. вероятность выхода из строя обслуживающего канала;
5. структура обслуживающей системы.
Для аналитического описания характеристик процедуры обслуживания оперируют понятием «вероятностное распределение времени обслуживания требований».
Пусть:
Si – время обслуживания i-го требования;
E(S) – среднее время обслуживания;
μ=1/E(S) – скорость обслуживания требований.
Следует отметить, что время обслуживания заявки зависит от характера самой заявки или требований клиента и от состояния и возможностей обслуживающей системы. В ряде случаев приходится также учитывать вероятность выхода из строя обслуживающего канала по истечении некоторого ограниченного интервала времени. Эту характеристику можно моделировать как поток отказов, поступающий в СМО и имеющий приоритет перед всеми другими заявками.
Коэффициент использования СМО
N·μ – скорость обслуживания в системе, когда заняты все устройства обслуживания.
ρ=λ/(Nμ) – называется коэффициентом использования СМО, показывает, насколько задействованы ресурсы системы.
Структура обслуживающей системы
Структура обслуживающей системы определяется количеством и взаимным расположением каналов обслуживания (механизмов, приборов и т. п.). Прежде всего следует подчеркнуть, что система обслуживания может иметь не один канал обслуживания, а несколько; система такого рода способна обслуживать одновременно несколько требований. В этом случае все каналы обслуживания предлагают одни и те же услуги, и, следовательно, можно утверждать, что имеет место параллельное обслуживани.
Пример. Кассы в магазине.
Система обслуживания может состоять из нескольких разнотипных каналов обслуживания, через которые должно пройти каждое обслуживаемое требование, т. е. в обслуживающей системе процедуры обслуживания требований реализуются последовательно. Механизм обслуживания определяет характеристики выходящего (обслуженного) потока требований.
Пример. Медицинская комиссия.
Комбинированное обслуживание – обслуживание вкладов в сберкассе: сначала контролер, потом кассир. Как правило, 2 контролера на одного кассира.
Итак, функциональные возможности любой системы массового обслуживания определяются следующими основными факторами:
вероятностным распределением моментов поступлений заявок на обслуживание (единичных или групповых);
мощностью источника требований;
вероятностным распределением времени продолжительности обслуживания;
конфигурацией обслуживающей системы (параллельное, последовательное или параллельно-последовательное обслуживание);
количеством и производительностью обслуживающих каналов;
дисциплиной очереди.
Основные критерии эффективности функционирования СМО
В качестве основных критериев эффективности функционирования систем массового обслуживания в зависимости от характера решаемой задачи могут выступать:
вероятность немедленного обслуживания поступившей заявки (Робсл=Кобс /Кпост);
вероятность отказа в обслуживании поступившей заявки (Pотк=Котк/Кпост);
Очевидно, что Робсл + Pотк=1.
Потоки, задержки, обслуживание. Формула Поллачека–Хинчина
Задержка – один из критериев обслуживания СМО, время проведенное заявкой в ожидании обслуживания.
Пусть:
Di – задержка в очереди требования i;
Wi=Di+Si – время нахождения в системе требования i.
Тогда показатели (если существуют)
(с вероятностью 1) – установившаяся средняя задержка требования в очереди;
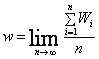(с вероятностью 1) – установившееся среднее время нахождения требования в СМО (waiting).
Пусть:
Q(t) – число требований в очереди в момент времени t;
L(t) – число требований в системе в момент времени t(Q(t) плюс число требований, которые находятся на обслуживании в момент времени t.
Тогда показатели (если существуют)
(с вероятностью 1) – установившееся среднее по времени число требований в очереди;
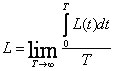(с вероятностью 1) – установившееся среднее по времени число требований в системе.
Заметим, что ρ<1 – обязательное условие существования d, w, Q и L в системе массового обслуживания.
Если вспомнить, что ρ= λ/(Nμ), то видно, что если интенсивность поступления заявок больше, чем Nμ, то ρ>1 и естественно, что система не сможет справиться с таким потоком заявок, а следовательно, нельзя говорить о величинах d, w, Q и L.
К наиболее общим и нужным результатам для систем массового обслуживания относятся уравнения сохранения
Следует обратить внимание, что упомянутые выше критерии оценки работы системы могут быть аналитически вычислены для систем массового обслуживания M/M/N (N>1), т. е. систем с Марковскими потоками заявок и обслуживания. Для М/G/l при любом распределенииG и для некоторых других систем. Вообще распределение времени между поступлениями, распределение времени обслуживания или обеих этих величин должно быть экспоненциальным (или разновидностью экспоненциального распределения Эрланга k-го порядка), чтобы аналитическое решение стало возможным.
Кроме этого можно также говорить о таких характеристиках, как:
абсолютная пропускная способность системы – А=Робсл*λ;
относительная пропускная способность системы –
Еще один интересный (и наглядный) пример аналитического решения – вычисление установившейся средней задержки в очереди для системы массового обслуживания M/G/1 по формуле:
.
В России эта формула известна как формула Поллачека–Хинчина, за рубежом эта формула связывается с именем Росса (Ross).
Таким образом, если E(S) имеет большее значение, тогда перегрузка (в данном случае измеряемая как d) будет большей; чего и следовало ожидать. По формуле можно обнаружить и менее очевидный факт: перегрузка также увеличивается, когда изменчивость распределения времени обслуживания возрастает, даже если среднее время обслуживания остается прежним. Интуитивно это можно объяснить так: дисперсия случайной величины времени обслуживания может принять большое значение (поскольку она должна быть положительной), т. е. единственное устройство обслуживания будет занято длительное время, что приведет к увеличению очереди.
Предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования. В большинстве случаев все параметры, описывающие системы массового обслуживания, являются случайными величинами или функциями, поэтому эти системы относятся к стохастическим системам.
Случайный характер потока заявок (требований), а также, в общем случае, и длительности обслуживания приводит к тому, что в системе массового обслуживания происходит случайный процесс. По характеру случайного процесса, происходящего в системе массового обслуживания (СМО), различают системы марковские и немарковские. В марковских системах входящий поток требований и выходящий поток обслуженных требований (заявок) являются пуассоновскими. Пуассоновские потоки позволяют легко описать и построить математическую модель системы массового обслуживания. Данные модели имеют достаточно простые решения, поэтому большинство известных приложений теории массового обслуживания используют марковскую схему. В случае немарковских процессов задачи исследования систем массового обслуживания значительно усложняются и требуют применения статистического моделирования, численных методов с использованием ЭВМ.
Рассмотрим непрерывные марковские цепи, которые характеризуют процессы гибели и размножения. Количество событий соответствует количеству каналов. S0 – событие «все свободны, нет занятых каналов»; S1 – один канал занят, и т. д. Таким образом имеем процесс, в котором каждому событию соответствует целое число, которое характеризует количество занятых каналов. Событие заключается в том, что количество занятых каналов может уменьшиться на 1, или увеличиться на 1.
Простейшая одноканальная модель
Простейшей одноканальной моделью с вероятностными входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид:
, где λ – интенсивность поступления заявок;
Плотность распределения длительностей обслуживания:
, где μ – интенсивность (скорость) обслуживания.
Потоки заявок и обслуживаний простейшие.
1-й случай. Поток заявок поступает в систему без очереди. Так называемая система с отказами.
Система имеет два состояния:
S0 – система не занята;
S1 – система занята.
Переход из состояния S0 в состояние S1 происходит с интенсивностью λ, из состояния S1 в состояние S0 – с интенсивностью μ.
Возможны два подхода к решению задачи.
1-й путь. С помощью уравнений Колмогорова
Здесь на самом деле только одно уравнение, т. к.
Начальное условие p0(0)=0– канал свободен.
Линейное неоднородное уравнение 1-го порядка (см. лекцию 2).
Решение имеет вид:
.
Видно, что данное решение имеет стационар
– вероятность того, что заявка будет обслужена.
Нетрудно убедиться, что для одноканальной СМО с отказами вероятность Р0(t) есть не что иное, как относительная пропускная способность системы.
Действительно, Р0(t) – вероятность того, что в момент t канал свободен и заявка, пришедшая к моменту tt, будет обслужена, а следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно Р0(t).
Вероятность того, что в обслуживании будет отказано 
.
Абсолютная пропускная способность канала
.
2-й путь. Статистическое моделирование с использованием метода Монте-Карло.
На практическом занятии рассмотрим этот путь и сравним результаты моделирования с теоретическим решением.
Приложение. Трансакты и их «семейства»
В некоторых программных средах, например, в отечественной системе Pilgrim [2], предназначенных для имитационного моделирования экономических процессов, используется понятие трансакта.
Трансакт – это формальный запрос на какое-либо обслуживание. Трансакт имеет набор динамически изменяющихся особых свойств и параметров. Пути следования трансакта по графу модели определяются логикой функционирования компонентов модели. Трансакт может порождать группы (семейства) других трансактов.
