Решение методом Ньютона системы тригонометрических уравнения узловых напряжений практически ничем не отличается от рассмотренного в общем виде в разделе 2.3.4. Придавая в (1) (см п. 2.3.5) индексу i — номеру узла значения i =1, 2, …, n, записываем систему уравнений, неизвестные в которой — фазовые углы и модули напряжений и сами уравнения для повышения вычислительной устойчивости рассматриваются в приводимом ниже порядке. Если в каждом независимом узле заданы 
, то получим систему из 2 n уравнений с 2 n неизвестными 
, 
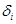, где n - число неизвестных комплексов напряжений узлов
Система тригонометрических уравнений Неизвестные:
узловых напряжений в форме баланса мощностей Фазовые углы
в развернутом виде:
(1) 
в матричной компактной форме записи:
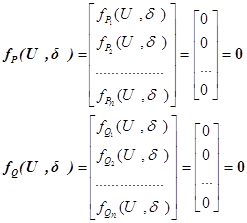(1) 
В системе линейных алгебраических уравнений относительно поправок к неизвестным (2) фигурируют значения частных производных от всех функций небалансов вначале активных а затем реактивных мощностей (1) по всем неизвестным, причем вначале находятся производные по фазовым углам, а затем по модулям напряжений. При таком порядке расположения уравнений и таком порядке расположения значений частных производных в матрице Якоби (2) на главной диагонали этой матрицы стоят наибольшие по модулю числа, что повышает вычислительную устойчивость решения системы уравнений (2).
Система линейных алгебраических уравнений относительно поправок к неизвестным Значения неизвестных на p -ом шаге
фазовым углам Δδ и модулям напряжений Δ U итераций
. Развернутая матричная форма 
Компактная матричная форма (2) (3)
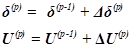
В компактной матричной форме записи система линейных алгебраических уравнений (2) записывается при помощи клеточных матриц. Здесь
, 
, 
, 
— матрицы-клетки значений частных производных функций небалансов активных и реактивных мощностей по фазовым углам и модулям напряжений в узлах. Они образуются, если в развернутой форме матрицы Якоби системы уравнений (2) провести две перегородки, одну — горизонтальную, после значений частных производных от функций небалансов активных мощностей, и одну — вертикальную, после дифференцирования функций небалансов по фазовым углам. Поправки к неизвестным и значения правых частей системы (2) также представлены в виде клеточных матриц- столбцов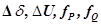 
.
Алгоритм решения системы уравнений узловых напряжений
1. Задаются значениями неизвестных фазовых углов и модулей напряжений 
на нулевом шаге итерационного процесса, которые можно обозначить как 
, поскольку номер шага итераций принимает значение p =1. Задаются также точностью расчёта ԑ, МВт, Мвар — т.е. допустимыми значениями невязок, небалансов мощностей в узлах.
2 Значения неизвестных подставляются в уравнения (1), рассчитываются невязки (небалансы) и сравниваются с заданной точностью (погрешностью).
Если неравенства выполняются – конец расчета, если нет – идти к п.3.
3 Значения неизвестных на нулевом шаге итераций 
подставляются в предварительно полученные выражения для частных производных, в результате рассчитываются элементы матриц Якоби и заканчивается формирование системы линейных алгебраических уравнений (2) относительно поправок 
.
4 Решается система линейных алгебраических уравнений (2) методом Гаусса с обратным ходом. Находятся значения поправок на первомшаге итераций 
(p =1) и уточненные значения неизвестных согласно (3).
5 
Идти к п.2.
Особенности решения систем уравнений узловых напряжений методом Ньютона
1 Так как многоразовое вычисление тригонометрических функций sinδ i, cosδ i требует значительного увеличения машинного времени, в некоторых программах используют замену неизвестных δ i на неизвестную 
. Полученная таким образом система нелинейных уравнений с неизвестными Ui,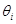 
решается без использования тригонометрических функций, что значительно ускоряет расчет. Значения фазных углов рассчитываются после окончания итерационного процесса с использованием соотношений:
2 Для повышения надежности решения в части генераторных узлов в качестве независимых параметров режимов задают 
. Пусть число таких узлов, называемых опорными или балансирующими по Q, равно m 1. Число неизвестных модулей напряжений Ui равно n - m 1 и фазовых углов 
, общее число неизвестных равно 2 n - m 1.Тогда матрица Якоби представляет собой квадратную матрицу, имеющую порядок 2 n - m 1.
3 Матрица Якоби системы уравнений установившегося режима слабо заполнена, как и матрица Y у. Поэтому в расчетах на ЭВМ на каждом шаге метода Ньютона используются способы сохранения слабой заполненности матрицы производных.
Важнейшее преимущество метода Ньютона в расчётах установившихся режимов на ЭВМ – быстрая квадратичная сходимость и возможность учета слабой заполненности матрицы производных. Время расчета по этому методу возрастает с увеличением числа узлов энергосистемы в среднем немного быстрее, чем по линейному закону, в то время как в методе Гаусса-Зейделя время расчёта растет приблизительно пропорционально квадрату числа узлов.
Недостатки метода:
1 Большая чувствительность к выбору начального приближения неизвестных.
2 В системе с плохо обусловленной матрицей Якоби, метод Ньютона может не сходиться. Плохая обусловленность может явиться следствием сильной неоднородности параметров схемы замещения энергосистемы, а также близости искомого установившегося режима к границе апериодической устойчивости энергосистемы. Сходимость в основном определяется свойствами матрицы 
.
3 Необходимость на каждом шаге рассчитывать элементы матрицы Якоби.
4 Невозможность вести расчёты при комплексных неизвестных и коэффициентах.
Улучшение сходимости метода Ньютона
Улучшение сходимости метода Ньютона достигается:
1. Введение в вычислительную схему параметра t (метод «по параметру»):
.
Существуют различные алгоритмы выбора параметра 
, например, параметр выбирается из условия достижения на каждом шаге метода Ньютона минимума суммы квадратов невязок—т.н. градиентный метод). Методы «по параметру» широко используются в расчётах установившихся (особенно тяжелых) режимов сложных электрических систем. Эти методы позволяют при несовместных исходных данных решать задачу введения режима в допустимую область.
Метод по параметру характеризуется быстрой сходимостью и относительно небольшими потребностями машинного времени. Недостаток метода – сложность, требующая от программиста высокой квалификации.
2 Другим способом улучшения сходимости метода Ньютона является учет кроме линейного члена разложения функций 
в ряд Тейлора членов с производными более высокого порядка.
3 Недостаток метода Ньютона —большая чувствительность к выбору начального приближения неизвестных преодолевается введением хороших начальных фаз напряжений узлов энергосистемы. В ряде случаев используется алгоритм, в котором расчет проводится, начиная с метода Гаусса-Зейделя. После нескольких итерации по этому методу осуществляется переход на метод Ньютона.
Важным при анализе установившихся режимов энергосистем является вопрос единственности решения уравнений установившегося режима. Чтобы режим сходился к технически правильному решению, для части мощных электростанций в качестве независимых параметров режима задаются
.
2.5 РАСЧЕТЫ УСТАНОВИВШИХСЯ РЕЖИМОВ СИСТЕМ БОЛЬШОЙ СЛОЖНОСТИ
При расчетах установившихся режимов электрических сетей и систем большой сложности во многих случаях практически невозможно и нецелесообразно вести расчёт применительно к полной схеме замещения, отражающей все элементы системы.
В таких условиях чаще всего находит применение эквивалентирование большей части системы, реже – разделение её на подсхемы.
При эквивалентировании, используемом в промышленных программах комплексах для расчётов установившихся режимов, большая часть схемы замещения системы упрощается перед выполнением расчетов с целью уменьшения числа узлов и ветвей.
При разделении схемы на подсхемы расчёт режима ведется на основе нескольких групп уравнений, часть из которых описывает режимы выделенных подсхем, а часть характеризует взаимную связь режимов этих подсхем.
В основу эквивалентирования схем замещения для расчетов установившихся режимов положен алгоритм прямого хода метода Гаусса исключения неизвестных из системы уравнений узловых напряжений. Рассмотрим небольшой участок схемы замещения системы.
При исключении к-го узла, связанного с узлами 
, звезда проводимостей (сопротивлений) этого узла преобразуется в треугольник с проводимостями сторон
,
где 
- собственная узловая проводимость узла к.
К -ый шаг прямого хода метода Гаусса, на котором из системы уравнений узловых напряжений исключается неизвестное 
, равносилен в электрическом смысле преобразованию звезды сопротивлений этого узла в эквивалентный треугольник.
Подобные преобразования схем замещения являются эквивалентными, поскольку напряжения и токи в других узлах и ветвях остаются неизменными.
Рассмотренный способ преобразования составляет основу эквивалентирования для расчётов установившихся режимов. Все энергосистемы, примыкающие к энергосистеме, для которой проводится расчёт установившегося режима эквивалентируются небольшим числом фиктивных узлов и ветвей, соединяющих эквивалентируемую часть системы с т.н. узлами примыкания. Параметры эквивалентируемых узлов и ветвей и являются результатом работы программы эквивалентирования. Следует отметить, что при таком эквивалентировании эквивалентная схема не адекватна исходной по величине сумарных потерь мощности.
