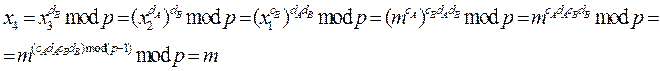Кіріспе
Курстық жұмыстың мақсаты - крипографиялық әдіспен телекоммуникациялық жүйелердегі ақпараттарды қорғау жүйесін математикалық негіз арқылы тұрғызуды студенттерге таныстыру. Курстық жұмыс мәліметтерді қорғауды жүзеге асырудың әдістері мен принциптері туралы студенттердің жүйеленген ойының қалыптасуына бағытталған.
Курстық жұмыс жабық кілтпен шифрлеу жүйесін оқытуға арналған. №1 тапсырма жабық кілтпен шифрлеуге арналған. RSA алгоритмдері қарастырылады, сонымен қатар хеш-функциялы қолдануы бар электронды қолтаңбалар бойынша есептеулер ұсынылады.
№2 тапсырма ассиметриялық шифрлеуге немесе ашық кілт арқылы шифлеуге арналған. Дифи –Хелман, Шамир, Эль-Гамаль алгоритмдері қарастырылады..
Тапсырма
1.1 Тапсырма
Симметриялы емес шифрлеу –дешифрлеу.
Келесі таратуға арналған ақпаратты RSA әдісі арқылы шифлеу керек.
Құпия кілтті екі нұсқамен, ұсынылған әдіспен және кеңейтілген Эвклид алгоритмімен генерирлеу керек.
Тапсырманың нұсқасы студенттік билеттің соңғы сандарымен анықталады. I нөмері арқылы (соңғы саннынң алдындағы сан) студент шифлеу үшін хабарды таңдайды,ал j –бойынша осы алгоритмнің жүзеге асуына керек р және q сандарын таңдайды.
Кесте -Бастапқы мәліметтер
| i | |||||
| Хабар | Принтер | Интеграл | Минус | Модуль | Плюс |
| j | |||||
| p q | 7.11 | 5.17 | 3.11 | 11.19 | 13.17 |
Кестенің жалғасы
| i | |||||
| Хабар | Число | Дробь | Корень | Остаток | Степень |
| j | |||||
| p q | 7.17 | 5.11 | 7.13 | 11.17 | 5.13 |
Тапсырманы орындауға арналған әдістемелік нұсқаулар
RSA алгоритмі қолданылатын, ашық кілтпен шифлеу әдісі - симметриялы емес шифрлеу-дешифлеу әдістерінің ең кең тараған түрі болып табылады.
Әртүрлі АКЖ-нің (ашық кілт жүйесі) саны көп болғанына қарамастан, 1977 жылы құрастырылған және өзінің құрастырушыларының Рона Ривест, Ади Шамир және Леонард Эйдельман есімдерімен аталған RSA криптожүйесі, әлдеқайда кең қолданысқа ие.
Олар санау жағдайында жай үлкен сандарды табу оңай жүзеге асатындығын қолданды, бірақ осындай екі санның нәтижесін көбеіткішке жіктеу практикада мүмкін емес. RSA шифрінің ашылуы осындай жіктеуге эквивалентті екендігі дәлелденген (теорема Рабина). Сондықтан шифрді ашу үшін кез келген кілт ұзындығына төмен бағалы операциялар санын беруге болады, және қазіргі компьютерлердің өнімділігін ескере отырып, оған кететін уақытты да бағалау керек.
Басқа он шақты АКЖ сұлбаларының қасында RSA алгоритмінің қорғалуын бағалауына кепілдік беруі, оның атақты болу себептерінің бірі. Сондықтан RSA алгоритмі банктік компьютерлік желілерде, әсіресе жойылған клиенттермен (кредиттік карталарға қызмет көрсету) жұмыс істеу үшін қолданылады.
Осы алгоритмнің негізіне қойылған математикалық нәтижелерді қарастырайық.
1 Теорема. (Ферманың кіші теоремасы.)
Егер р – жай сан,онда
xp-1 = 1(mod p) (1)
р-ға қатысты жай сан болатын,кез келген х үшін және
xp = x(mod p) (2)
кез келген х үшін.
Дәлелдеу. xp үшін (1) және (2) теңдеулерінің әділеттілігін дәлелдеу жеткілікті. Дәлелдеуді индукция әдісімен жүргіземіз.
(3) теңдеу х=0 және 1 болғанда орындалатындығы анық.Ары қарай
xp = (x –1 + 1)p = C(p,j)(x –1)j = (x –1)p + 1(mod 2),
0<j<р болғанда C(р,j)=0(mod р). Осы теңсіздікті ескере отырып және дәлелдеу әдісінің ұсыныстарымен индукция теоремасы дәлелденді.
Анықтама. Эйлер функциясы φ(n) деп теріс емес бүтін,кіші n және n ге қатысты жай сандарды айтамыз.
1.2 Кесте – Бастапқы мәліметтер:
| n | |||||||||||
| φ(n) |
2 Теоремасы. Егер n = рq, (р және q – бір біріне қатысты жай сандар),онда
φ(n)=(р-1)(q-1)
3 Теорема. Егер n = рq, (және q – бір біріне қатысты жай сандар) және х –р және q қатысты жай сан, онда
xφ(n) = 1(mod n)
Салдар. Егер n = рq, (және q – бір біріне қатысты жай сандар) және е (n)-ге қатысты жай сан, онда өрнек
Eв,n : xxв(mod n)
Zn-ге қатысты өзара бірмәнді болып табылады.
Егер е саны f(n) санына қатысты жай сан болса,онда келесі өрнекке тең болатын, бүтін d санынының бары анық,
ed ≡ 1 (mod φ(n)) (3)
RSA атақты алгоритмі осы математикалық фактілерге негізделген.
n = рq тең болсын, мұндағы р және q – әртүрлі жай сандар.Егер e және d онда Еe,n және Еd,n өрнектері Zn-ге инверсті болып келеді. Егер e, d, р, q сандары белгілі болса, Еd,n өрнегі Еe,n сияқты оңай есептеледі.
Егер e және n сандары белгілі болып, бірақ р және q сандары белгісіз болса,онда Еe,n біржақты функция болады; Еd,n-ды берілген n бойынша табу, n жіктегенге тең болады. Егер р және q – жеткілікті түрде үлкен жай сандар болса,онда n-ді жіктеу мүмкін емес. Осы RSA шифрлеу жүйесінің негізіне қойылған.
RSA шифржүйесі
Қазіргі кезде ең кең таралған ашық кілтпен шифлеу жүйесі,RSA жүйесі болып табылады.
n = pq – p, q екі үлкен санның туындысы түрінде ұсынылатын бүтін сан болсын. Алгоритмнің шифленуі мен шифрді ажыратуын анықтайтын e және d сандары сәйкесінше,келесі шартқа жауап беруі керек
ed ≡ (mod φ(n)), (1)
мұндағы φ(n) = (p-1)(q-1) – n санына қатысты Эйлера функциясының мәні. k = (n,p,q,e,d) – k1 = (n,e) ашық кілтінен және құпия k2 = (n,p,q,d) кілтінен тұратын, таңдап алынған кілт болсын. M – ашық мәтіннің блогы болып және C –шифрленген мәтін блогына сәйкес келетін болсын.Сонда шифлеу және шифрді ажырату ережелері келесі формулалармен анықталады:
С = Ek (M) =Me (mod n), Dk(C) = Cd (mod n) (2)
(2) формуланың Dk(C) = M өрнегімен сәйкес екендігін ескереміз.
(1) шартты қанағаттандыратын, e және d мәндерін табу кезінде, е санын φ(n) санымен өзара жай болатындай етіп таңдайды, ал d-ның мәнін келесі теңдеуден анықтайды
φ(n)x + ed = 1 (3)
Жалпы жағдайда (3) теңдеу ax + by = c түріне сәйкес келеді (мұндағы a = φ(n), b = e, y = d) және ол Диафантты теңдеу деп аталады.
Ол теңдеудің шешімі
y = (–1)μ · aμ-1 · x = (–1)μ+1 · b μ-1 (4)
a/b қатынасын тізбекті бөлшек түрінде жіктеу көмегімен алуға болады:
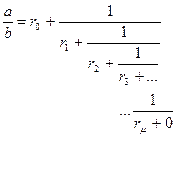
мұндағы μ – тізбекті бөлшектің реті,яғни қалдығы нөлге болатын, бөлшек коэффициентінің индексі,
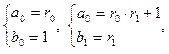
(5)
үшіншіден бастап қалған мүшелерінің барлығына келесі теңдіктер орындалады
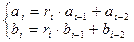(6)
Осылай (3) теңдеуді шешу үшін a/b қатынасын бөлшекті тізбек ретінде ұсынып, r0, r1…rμ және μ. мәндерін анықтау керек. Содан кейін (4) – (6) теңдіктердің сәйкес болуы арқылы ai, bi мәндері, сонымен қатар x және y мәндері анықталады.
Мысал
p = 17, q = 31 қолдана отырып, RSA аббревиатурасын шифлейік.Ол үшін n = pq = 527 және μ(n) = (p-1)(q-1) = 480 мәндерін есептейік. e саны ретінде, μ(n) санымен өзара жай болып келетін санды таңдаймыз,мәселен, e = 7. μ(n)x + ey = 1 қатынасын қанағаттандыратын,бөлшек тізбегі арқылы бүтін x және y сандарын табамыз. 480x + 7y = 1 түрінде жазамыз
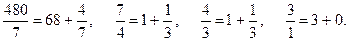
сәйкесінше,
μ = 3, a0 = 68, b0 = 1, a1 = 69, a2 = 1·69 + 68 = 137, b2 = 1·1 + 1 = 2.
осылай, x = –2, y = –137.
–137 (mod 480) = 343 тең болғандықтан, онда d = 343.
тексеру
7 · 343 = 2401 = 1(mod 480).
Енді берілген хабарды 0…526 интервалында құралатын сандардың тізбегі ретінде ұсынамыз.Ол үшін R, S және A әріптерін бестік екілік векторлармен, яғни олардың алфавиттегі реттік номерлерінің екілік жазбасын қолданып,кодтаймыз:
R = 18 = (10010), S = 19 (10011), A = 1 (00001).
Сонда RSA = (100101001100001). 0…526 берілген интервалында жіктеліп, келесі көріністі аламыз:
RSA = (100101001), (100001) = (M1 = 297, M2 = 33).
Содан кейін M1 және M2 мәндерін шифлейміз:
C1 = Ek (M1) = M1в = 2977 (mod 527) = 474
Мұнда біз мына теңдікті қолдандық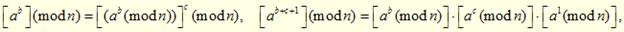 
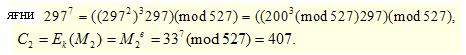
Нәтижесінде шифромәтінді аламыз: С1 = 474, С2 = 407.
Шифрді ажырату кезінде келесі әрекеттердің тізбегін орындау керек. Біріншіден, есептеу керек
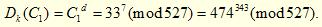
343 = 256 + 64 + 16 + 4 + 2 + 1 есептеуіне қарағанда дәрежеге шығарып қолдану ыңғайлы екенін ескереміз. Осы айтылғанның негізінде келесі өрнектерді аламыз:
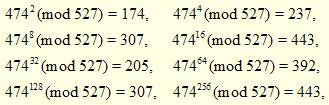
Осыған сәйкес
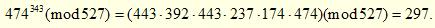
Және сол сияқты
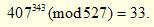
Әріптік жазуға қайта оралып, RSA қайта шифлеуінен кейін аламыз.
2.2.т. Шамир алгоритмінде толық суреттелген, Эвклид кеңейтілген алгоритмін қолдана отырып, жабық кілттің генерациясын жүргізу керек.
1.2 Тапсырма
1.2 Хештау және құжаттардың сандық қолтаңбасы.
1.1 тапсырмасының мәліметтерін қолдана отырып, МККТТ Х.509 ұсынысынан алынған Н хеш – функциясының көмегімен М хабарламасы үшін m хеш – кодын есептеу. Н0 инициализациялау векторын нөлге тең деп алу.
Есептелген m хеш – коды мен құпия кілт d-ны қолданып, М электрондық құжатының астындағы сандық қолтаңбаны RSA әдісімен анықтау.
Сандық қолтаңбаның сұлбасын жұмыс істеуінің толық сипаттамасымен келтіру қажет.
МККТТ Х.509 хеш – функциясын келесі түрде жазамыз:
Hi=[(Hi-1 Å Mi)2] (mod n), мұнда i=l,n, H0 – инициализациялау векторы, Мi =М1,М2,М3…,Мn - блок ұзындығы.
Барлық блоктарды ортасынан бөледі де әрбір жартыға тең бірлердің саны қосылады. Осылайша түрленген блоктармен интеграциялық амалдар орындалады.
p=3, q=11 параметрлері бар Х.509 хеш – функциясының көмегімен ПРЕДЕЛ хабарламасының хеш – кодын алу.
Хеш-кодты анықтау реті:
а) n=pq= 3*11=33 модулінің мәнін есептеу;
б)Хабарды орыс әліпбиінің әрітерінің саны ретінде ондық және екілік түрлерде келтіру:
П Р Е Д Е Л
16 17 6 5 6 12
00010000, 00010001, 00000110, 00000101, 00000110, 00001100:
в) Байтты ортасынан бөліп, жартыбайттың басына бірлерді қосу және Мi хешталатын блоктарын алу:
1№3 Кесте-Бастапқы мәліметтер:
| M1 | M2 | M3 | M4 | M5 | M6 |
| M7 | M8 | M9 | M10 | M11 | M12 |
г) Интеративті қадамдарды орындау:
Бірінші интерация
| М1 | |
| Å | |
| Н0=0 | |
| Н0 Å М1 | 11110001=24110 |
| [(H0Å M1)2] (mod 33) | 2412 mod 33 = 10 |
| Н1 | 1010=00001010 |
Екінші интерация
| М2 | |
| Å | |
| Н1 | |
| Н1 Å М2 | 11111010=25010 |
| [(H1Å M2)2] (mod 33) | 2502 mod 33 = 19 |
| Н1 |
Үшінші интерация
| М3 | |
| Å | |
| Н2 | |
| Н2 Å М3 | 11100010=22610 |
| [(H2Å M3)2] (mod 33) | 2262 mod 33 = 28 |
| Н3 |
Төртінші интерация
| М4 | |
| Å | |
| Н3 | |
| Н3 Å М4 | 11101101=23710 |
| [(H3Å M4)2] (mod 33) | 2372 mod 33 = 6 |
| Н4 |
Бесінші интерация
| М5 | |
| Å | |
| Н4 | |
| Н4 Å М5 | 11110110=24610 |
| [(H4Å M5)2] (mod 33) | 2462 mod 33 = 15 |
| Н5 |
Алтыншы интерация
| М6 | |
| Å | |
| Н5 | |
| Н5 Å М6 | 11111001=24910 |
| [(H5Å M6)2] (mod 33) | 2492 mod 33 =18 |
| Н6 |
Жетінші интерация
| М7 | |
| Å | |
| Н6 | |
| Н6 Å М7 | 11100010 = 22610 |
| [(H6Å M7)2] (mod 33) | 2262 mod 33 = 28 |
| Н7 |
Сегізінші интерация
| М8 | |
| Å | |
| Н7 | |
| Н7 Å М8 | 11101001= 233 |
| [(H7Å M8)2] (mod 33) | 2332 mod 33 = 2 |
| Н8 |
Тоғызыншы интерация
| М9 | |
| Å | |
| Н8 | |
| Н8 Å М9 | 11110010 = 24210 |
| [(H8Å M9)2] (mod 33) | 2422 mod 33 = 11 |
| Н9 |
Оныншы интерация
| М10 | |
| Å | |
| Н9 | |
| Н9 Å М10 | 11111101 = 253 |
| [(H9Å M10)2] (mod 33) | 2532 mod 33 = 22 |
| Н10 |
Он бірінші интерация
| М11 | |
| Å | |
| Н10 | |
| Н10 Å М11 | 11100110 =23010 |
| [(H10ÅM11)2] (mod 33) | 2302 mod 33 = 32 |
| Н11 |
Он екінші интерация
| М12 | |
| Å | |
| Н11 | |
| Н11 Å М12 | 11011100 = 22010 |
| [(H11ÅM12)2] (mod 33) | 2202 mod 33 = 22 |
| Н12 |
Осылайша, бастапқы ПРЕДЕЛ хабарламасы m=22 хеш-кодына ие.
Сандық қолтаңбаны есептеу үшін келесі формуланы қолданамыз:
S=md (mod n) = 223 mod 33 = 22
(M, S) жұбы қабылдаушыға S сандық қолтаңбасы қойылған М электрондық құжаты ретінде жіберіледі, мұндағы қолтаңба S құпия кілт d-ның иесімен жасалған.
(M, S) жұбын алған соң қабылдаушы М хабарының хеш-кодын екі әдіспен анықтайды:
1) m’ хеш – кодын е ашық кілті көмегімен S қолтаңбасының криптографиялық түрлендірілуін қолданып қалпына келтіреді:
m’=Se (mod n) =227 mod 33 = 22
2) Сол хеш – функцияның көмегімен қабылданған хабардың хешталу нәтижесін табады: m=H(M) =22.
Есептелген m’ және m мәндері тең болса, онда қабылдаушы (M, S) жұбын түпнұсқа деп мойындайды.
Бақылау сұрақтары
1. Ашық кілтті шифрлеу жүйесін қолданатын құпия байланысты ұйымдастырудың принципиалды сұлбасын суреттеңіз.
2. Сандық қолтаңбамен расталған құжаттармен алмасуды ұйымдастырудың принципиалды сұлбасын суреттеңіз.
3. Құжаттардың сандық қолтаңбасын есептеу кезінде жарамды хеш-функцияларға қойылатын негізгі талаптарды атап өтіңіз.
4. Түпнұсқалылығы сандық қолтаңбамен расталған шифрленген хабарларды RSA криптожүйесі арқылы таратуды қалайша ұйымдастыруға болады? Мысалдар келтіріңіз.
Тапсырма
2.1 Тапсырма
Ашық кілтті Диффи-Хеллман жүйесі
Диффи-Хеллман (DH) әдісімен бес абонент үшін құпия кілттерді генерациялаңыз. Ол үшін 1 кестеден құпия кілттің х мәнін алыңыз. Ашық кілттің сәйкес мәндерін анықтаңыз және нәтижелерді кестеге енгізіңіз. Тапсырманың нұсқасы i (соңғысының алдындағы сан) және j (сынақ кітапшасының соңғы саны) нөмірлері – бұл алгоритмді іске асыру үшін х саны. j саны – х санын таңдаудағы екінші абонент үшін бастапқы нөмір. Бес абонентпен байланысу үшін х-ті сынақ кітапшасының соңғы санымен циклдік процедура бойынша таңдаймыз. Мысалы, сынақ кітапшасындағы сандар (15). Бірінші абонент үшін x=11 таңдаймыз, себебі i =1. Екінші абонент үшін екінші сан бойынша x =29, себебі j= 5. Үшіншісі үшін (j +1)=i формуласы бойынша x= 31 аламыз, себебі j =6. Төртіншісі үшін x = 37, j =7. Бесіншіге x = 39 таңдаймыз, өйткені j=8. Мысалы, егер соңғы сан (27) бестен үлкен - j =7 болсын. Онда x = 31,37, 39,41, 7 таңдаймыз.
Ұсынылатын мәндер p = 30803, g = 2.
2.1 Кесте - Бастапқы мәліметтер:
| I | |||||
| x |
| I | |||||
| x |
Тапсырманы орындауға арналған әдістемелік нұсқаулар
Ашық кілтті бірінші жүйе —Диффи-Хеллман жүйесі.
Бұл криптожүйені 70-жылдардың ортасында американдық ғалымдар Диффи (Whitfield Diffie) және Хеллман (Martin Hell-man) ашты және криптография мен оның практикалық қолданылуында нағыз революцияға әкелді. Бұл қорғалған арналар бойынша таратылатын құпия кілттерді қолданбай-ақ ақпаратты қорғауға мүмкіндік берген бірінші жүйе. Мұндай жүйелерді қолданатын сұлбалардың бірін көрсету үшін N қолданушысы бар байланыс желісін қарастырайық, мұндағы N-үлкен сан. Олардың әрбір жұбы үшін құпия байланысты ұйымдастырғымыз келеді делік. Егер біз құпия кілттерді үлестірудің қарапайым жүйесін қоладанатын болсақ, онда абоненттердің әр жұбы өзінің құпия кілтімен қамтамасыз етілуі керек, яғни барлығы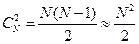 
кілт қажет болады.
Егер абоненттер 100 болса, онда 5000 кілт, егер 104 абонент болса, онда 5*107 кілт қажет болады. Көріп тұрғанымыздай, абоненттердің саны көп болғанда, оларды құпия кілттермен қамтамасыз ету жүйесі өте үлкен және қымбатқа түседі.
Диффи және Хеллман бұл мәселені кілттерді ашық тарату және есептеу арқылы шешті. Енді олар ұсынған жүйені суреттейік.
А,В,С,... абонеттері үшін байланыс жүйесі құрылсын. Әрбір абоненттің өзінің құпия және ашық ақпараты бар. Бұл жүйені ұйымдастыру үшін үлкен жай сан р және {1, 2, ∙ ∙ ∙,р — 1} қатарындағы сандар g mod p – ның әртүрлі дәржесінде келтірілетін әлдебір g саны таңдалады, 1 < g < р-1 (g-ны табудың әр түрлі тәсілдері бар, солардың бірі төменде көрсетіледі). р мен g сандары барлық абоненттерге белгілі.
Абоненттер құпияда сақталатын Xa,Xb,Xc үлкен сандарын таңдайды (әдетте мұндай таңдауды кездейсоқ сандар бергішін қолданып, кездейсоқ жасау ұсынылады). Әрбір абонент басқа абоненттерге ашық таратылатын сәйкес Ү санын анықтайды,
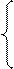YА = gXa mod р,
YB = gXb mod р.. (1)
Yс = gXc mod р.
Нәтижесінде келесі кестені аламыз.
2.2 Кесте- Диффи-Хеллман жүйесіндегі абонеттердің кілттері
| Абонент | Секретное число | Открытый ключ | Закрытый ключ |
| A B C | XA XB XC | YA YB YC | ZAB, ZAC ZBA, ZBC ZCA, ZCB |
А абоненті В абонентімен байланыс сеансын ұйымдастыруды шешті делік және екеуіне де 2 –кестедегі мәліметтер белгілі. А абоненті В – ға ашық арнамен хабар жіберетіндігін хабарлайды. Кейін А келесі мәнді есептейді
ZAB = (YB)ХА modp (2)
А-дан басқа ешкім мұны істей алмады, себебі ХА саны құпия.
Өз кезегінде В абоненті
ZBA = (YA)XBmodp (3)
мәнін табады.
1-суретте Диффи-Хеллман жүйесіндегі кілттерді алмасу сұлбасы көрсетілген.
Енді жоғарыда айтылған р санын таңдау есебіне тоқталайық. Егер g еркін таңдалатын болса, онда бұл есеп g – 1 санын жай сандарға жіктеумен байланысты қиын есеп болуы мүмкін. Мәселен, қарастырылған жүйенің жоғары тұрақтылығын қамтамасыз ету үшін g - 1 санында міндетті түрде жай үлкен көбейткіш болуы керек. Сондықтан келесі әдісті қолдану жиі ұсынылады.
р=2q+1 (мұндағы q- жай сан)
теңдігі орындалатындай р саны таңдалады және
1 < g < р - 1 и gq mod р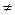 
1
теңсіздігі қанағаттандырылуы қажет.
Жүйе криптоанализге тұрақты болуы үшін р санын өте үлкен етүп таңдау қажет.
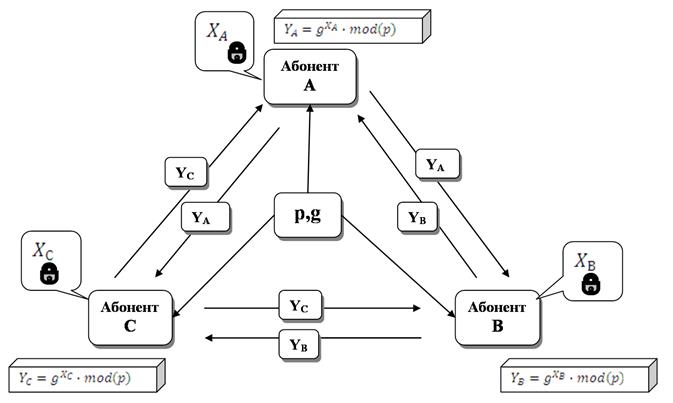
1 Сурет - Диффи-Хеллман жүйесіндегі кілттермен алмасу сұлбасы
Мысал
g = 43 болсын. р параметрін таңдайық. q=17 401 алып көрейік.
Сәйкесінше р=2*17 401+1=34 803. Тексерейік: 4317401 mod 34 803 = 17 746. Қажет шарттар орындалады, яғни мұндай р келеді. Сонымен, біз мы р = 34 803, g = 43 параметрлерін таңдадық. Енді әрбір абонент құпия санды таңдайды және оған сәйкес ашық санды есептейді. ХA = 7, ХB = 13 таңдалсын. YA = 437 mod 34 803 = 11 689, YB = 4313 mod 34 803 = 14 479 анықтаймыз. А мен В ортақ құпия кілтті жасағылары келсін делік. Ол үшін А ZAB = 144797 mod 34 803=6 415, ал В ZBA = 11 68913 mod 34 803 = 6 415 есептейді. Енді олар арнамен жіберілмеген 6 415 ортақ кілтіне.
Бақылау сұрақтары
1. Жабық кілтті басқа алгоритмдердің алдында Диффи-Хеллман жүйесі қандай артықшылықтарға ие?
2. Диффи-Хеллман жүйесіне қысқаша сипаттама беріңіз.
3. Құпия кілттерді есептеуде қажетті р санын неліктен үлкен етіп таңдау қажеттілігін түсіндіріңіз?
2.2 Тапсырма
Шамир алгоритмі бойынша шифрлеу
3-кестеден m хабарының және р-ның мәндерін алып, үш абонент үшін Шамир алгоритмі бойынша хабарды шифрлеу. і нөмірі бойынша (соңғысының алдындағы сан) студент шифрленетін хабарды, j бойынша – осы алгоритмді іске асыруға арналған р санын таңдайды. Басқа абоненттер үшін мәліметтерді (I + 1) және (G + 1) процедурасына сәйкес циклді жүргізу. Мысалы, сынақ кітапшасының соңғы сандары - (26). Үш абонент үшін (хабар,р) - (16,49), (18,51), (20,53) таңдаймыз.
Кесте 3 – Бастапқы мәліметтер:
| I | |||||
| Хабар | |||||
| G | |||||
| p |
| I | |||||
| Хабар | |||||
| G | |||||
| p |
№2.2 тапсырманы орындауға арналған әдістемелік нұсқаулар
Шамир (Adi Shamir) ұсынған бұл шифр қорғалған арналары және құпия кілттері жоқ, әрі, мүмкін, ешқашан бірін-бірі көрмеген адамдарға, ашық байланыс желісі бойынша құпия хабарларды алмасуды ұйымдастыруға мүмкіндік беретін болды. (Естеріңізхге сала кетейік, Диффи-Хеллман жүйесі тек құпия сөзді жасауға мүмкіндік береді, ал хабарды тарату үшін ол кілт болып қолданылатын басқа шифрді қолдануды қажет етеді).
Жүйені сипаттауға өтелік. А және В абоненттері байланыс желісі арқылы байланыссын. А абонентті В абонентіне ешқандай басқа абонент мазмұнын білмейтіндей етіп, m хабарды бергісі келеді. А кездейсоқ үлкен жай сан р таңдайды және оны В ға ашық түрде береді. Содан соң А екі санды сА және dA таңдайды, олар
сАdA mod (р - 1) = 1 (2.1) болуы тиіс.
Бұл сандарды А құпияда сақтайды және В абонентіне жібермейді. В да екі құпия санды св және dв таңдайды, олар
свdв mod (p - 1) = 1 (2.2)
Бұдан соң А үшсатылы протоколды қолданып өзінің m хабарын береді. Егер m < р (m сан ретінде қарастырылады) болса, онда т хабары лезде жіберіледі. Ал егер m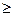 
р болса, онда хабар m1, m2,..., mt түрінде беріледі. Мұндағы mi < р, және m1, m2,..., mt тізбектеліп беріледі. Осыған байланысты әрбір mi кодалау үшін кездейсоқ жаңа жұпты таңдаған дұрыс – қарсы жағдайда жүйенің сенімділігі төмендейді. Қазіргі кезде ереже ретінде мұндай шифр сандарды жіберу үшін қолданылады. Мысалы: құпия кілт р-дан аз делік. Сонымен, біз m < р жағдайды ғана қарастырамыз.
Протоколды сипаттау.
1 Қадам. А х1 =mСА mod p (2.3) санын есептеп шығарады. Мұнда m —бастапқы хабар, және х1 –ді В ға жібереді.
2 Қадам. х1 хабарды алған В х2 = х1CB mod p (2.4) санын есептеп шығарады және х2 ні А ға береді.
3 Қадам. А х3 = х2dA mod p (2.5) есептеп шығарады және оны В ға береді.
4 Қадам. х3 хабарды алған В х4 = x3dB mod p (2.6) санын есепеп шығарады.
Шамир алгаритмі бойынша кілт алмасу сұлбасы 2-суретте көрсетілген.
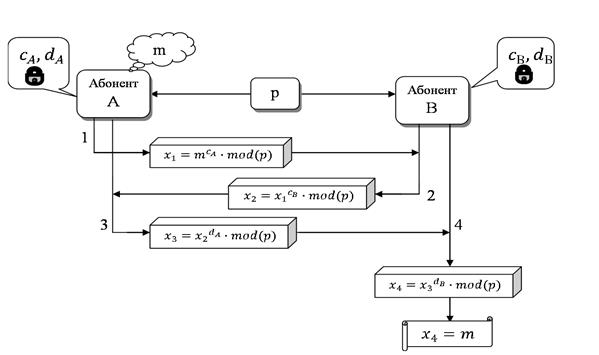
Сурет 2 – Шамир жүйесіндегі кілт алмасу сұлбасы
Бекіту (Шамир протоколының қасиеттері):
1) х4 = m, яғни протоколды тарату барысында шынында да А және В дан бастапқы хабар беріледі;
2) Қиратушы қандай хабар берілгенін біле алмайды.
Дәлелдеу. Алғашында кез-келген е 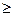0 бүтін сан, е = k(р — 1)+r түрінде берілетінін байқайық, мұнда r = е mod (p - 1). Сондықтанда Ферма теоремасына негізделген.
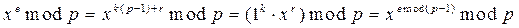(2.7)
Бекітудің бірінші пункті келесі теңдек тізбегінен пайда болады.
