1. По формулам табл. 1.1 находим эквивалентный радиус расщепления проводов.
r0 - радиус провода; 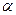 - шаг расщепления фазы
- шаг расщепления фазы

 ;
;
β =2; 
2. Для заданой системы проводов вычислить потенциальные коэффициенты 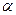 . Причем
. Причем 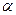 kk называют собственными потенциальными коэффициентами k-го провода. Потенциальный коэффициент
kk называют собственными потенциальными коэффициентами k-го провода. Потенциальный коэффициент 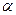 ik (i
ik (i 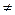 k) определяет составляющую потенциала k-го провода, создаваемую зарядом i - го провода,
k) определяет составляющую потенциала k-го провода, создаваемую зарядом i - го провода,
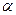 ik взаимные потенциальные коэффициенты проводов i и k.
ik взаимные потенциальные коэффициенты проводов i и k.
Коэффициенты 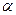 вычисляют
вычисляют
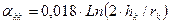 , М/пФ
, М/пФ
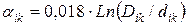 , М/пФ
, М/пФ
где hср = hk - 2f/3; f - стрела подвеса провода.
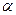 11=
11= 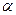 22=
22= 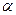 33=0,018∙Ln∙
33=0,018∙Ln∙  ;
;
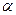 11=
11= 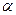 22=
22= 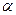 33=
33= 
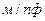 ;
;
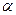 12=
12= 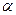 13=0,018∙Ln∙
13=0,018∙Ln∙ 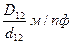 ;
;
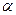 12=
12= 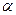 21=
21= 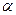 13=
13= 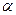 31=
31= 
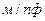
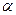 23=0,018∙Ln∙
23=0,018∙Ln∙  ;
;
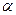 23=
23= 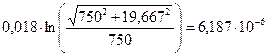
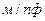
3. Вычислить емкостные потенциальные коэффициенты 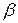 .
.
Для вычисления коэффициентов 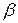 найдём определитель
найдём определитель  по формуле:
по формуле:

|



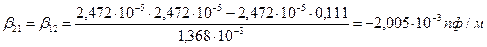
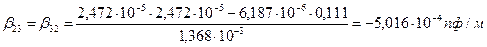

4. Определим рабочие емкости проводов трехфазной линии по формулам (1.4) при симметрии векторов в момент времени t, когда ось действительная совпадает с направлением вектора напряжения U1, тогда напряжение в фазе 1 максимально и равно U, а в фазах 2 и 3 - 0,5U. Таким образом, средняя фаза С1 обладает большей напряженностью, а С2 = С3.
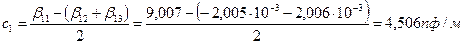

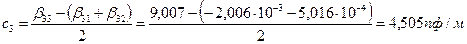
5. По заданным напряжениям полюсов или фаз и известным рабочим емкостям вычислим удельные заряды проводов. При этом амплитуда фазного напряжения находится

где 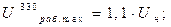
Тогда соответственно удельные заряды на проводах


6. Вычислим средние напряженности на поверхности расщепленных проводов по формулам (1.7), где n - число проводов в фазе.
 ;
;

7. По формулам табл.1.1 вычислим максимальные напряженности на поверхности проводов по зависимости (1.8)
Определим максимальную напряженность на поверхности проводов:

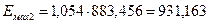
8. Рассчитаем приближенно напряженность поля на поверхности провода трехфазной линии, где рабочая емкость проводов 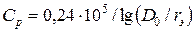 , пФ/м, где D0 = d; r э и k определяются по табл.1.1, а на среднем проводе Еmax, найденное по (1.9) повышается на 7%.
, пФ/м, где D0 = d; r э и k определяются по табл.1.1, а на среднем проводе Еmax, найденное по (1.9) повышается на 7%.

9. Находим значение критической напряженности коронного разряда на проводе заданной ЛЭП по зависимости(1.10)
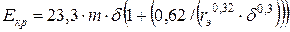 , кВ/см,
, кВ/см,
где m - коэффициент гладкости провода от 0,6 до 0,85; 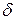 = 1,013; rэ - эффективный радиус провода.
= 1,013; rэ - эффективный радиус провода.

10. По сравнению результатов Еmax и Екр можно сделать вывод, что корона на проводах присутствует. Проводившееся в последние годы эксперименты позволили установить, что потери на корону и радиопомехи в первую очередь зависят от минимальной напряженности поля на поверхности провода, которая при заданном напряжении определяются радиусом провода уменьшает корону. Экономическое решение можно получить посредством применения расщеплённых проводов. Для расщеплённых проводов следует оптимально выбирать шаг расщепление провода. На возникновение местной короны влияют царапины, заусенцы, загрязнение на проводах. Во время выпадения осадков на проводе образуется сияние, именно это явление называется короной.
ЗАДАНИЕ 2.
ЗАДАЧА. Рассчитать и построить в координатах (U, x/ 1) огибающую максимальных градиентов вдоль обмотки двухобмоточного трансформатора при попадании на ввод его электромагнитной волны перенапряжения с прямоугольным фронтом и амплитудой U0. Обмотка трансформатора имеет n катушек, емкость каждой катушки относительно корпуса 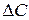 и между катушками
и между катушками  по всей единичной длине l обмотки (схема замещения обмотки трансформатора только по емкостям справедлива, когда на вход ее попадает крутая форма напряжения). В расчете свободной составляющей распределенного напряжения учесть первые три гармоники, амплитуды которых определятся по формулам:
по всей единичной длине l обмотки (схема замещения обмотки трансформатора только по емкостям справедлива, когда на вход ее попадает крутая форма напряжения). В расчете свободной составляющей распределенного напряжения учесть первые три гармоники, амплитуды которых определятся по формулам:
для трансформатора с заземленной нейтралью
 (2.1)
(2.1)
для трансформатора с изолированной нейтралью
 , (2.2)
, (2.2)
где k - натуральный ряд чисел; в (2.1) k -номер гармоники; в (2.2) (2•k - 1) - номер гармоники.
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА.
1. Найти коэффициент  по параметрам обмотки из табл.2.1.
по параметрам обмотки из табл.2.1.
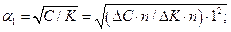 (2.3)
(2.3)
2. Построить начальное распределенное напряжение для схемы замещения обмотки трансформатора, принимая значение переменной величины x/ l = 0;
0,25; 0,5; 0,75; 1,0 для выражения
 (2.4)
(2.4)
3. Построить функцию напряжения в установившемся режиме для схемы замещения согласно режима нейтрали и переменной величины x/l.
4. Рассчитать амплитуду гармоники Аk, построить свободную составляющую распределенного напряжения Uсв1 в координатах x/l с учетом того, что если потенциалы в начале и в конце обмотки фиксированы (заземленная нейтраль), то имеем узлы высших гармоник в этих местах обмотки и целое число полуволн по всей ее длине; если потенциал фиксирован в начале обмотки и неопределен в конце (изолированная нейтраль), то имеем узел высших гармоник в начале и пучок их в конце обмотки и поэтому целое число четверть-волны напряжений по всей длине обмотки. Рассчитать первые три гармоники для любого режима нейтрали. Проверить полученную огибающую свободной составляющей напряжения путем разности амплитуд напряжений начального распределения и установившегося
 (2.5)
(2.5)
Если  и
и  отличаются друг от друга на 10% и более, то изменить основные параметры
отличаются друг от друга на 10% и более, то изменить основные параметры  уменьшить в 2-5 раз, а
уменьшить в 2-5 раз, а  увеличить в 2-3 раза и повторить расчет по п.п.2.4.
увеличить в 2-3 раза и повторить расчет по п.п.2.4.
5. Построить максимальную огибающую распределенного напряжения Umax по обмотке трансформатора как сумму векторов по абсолютной величине свободной составляющей и установившейся
 (2.6)
(2.6)
6. Сделать заключение по распределению  , где в начале или в конце обмотки трансформатора необходимо усилить изоляцию, чтобы исключить пробой её от набегающей волны перенапряжения и предложить мероприятия.
, где в начале или в конце обмотки трансформатора необходимо усилить изоляцию, чтобы исключить пробой её от набегающей волны перенапряжения и предложить мероприятия.
Таблица 2.1
Варианты исходных данных
| № | U0, кВ | n, шт | 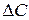 , пФ , пФ
|  , пФ , пФ
| режим нейтрали |
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. | |||||
| заземл. и изолир. |
Решение 2.
ЗАДАЧА. Рассчитаем и построим в координатах (U, x/1) огибающую максимальных градиентов вдоль обмотки двухобмоточного трансформатора при попадании на ввод его электромагнитной волны перенапряжения с прямоугольным фронтом и амплитудой U0 =250кВ. Обмотка трансформатора имеет n =25 катушек, емкость каждой катушки относительно корпуса 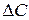 =25пФ и между катушками
=25пФ и между катушками  =900 пФ по всей единичной длине l обмотки (схема замещения обмотки трансформатора только по емкостям справедлива, когда на вход ее попадает крутая форма напряжения). В расчете свободной составляющей распределенного напряжения учтём первые три гармоники, амплитуды которых определятся по формулам:
=900 пФ по всей единичной длине l обмотки (схема замещения обмотки трансформатора только по емкостям справедлива, когда на вход ее попадает крутая форма напряжения). В расчете свободной составляющей распределенного напряжения учтём первые три гармоники, амплитуды которых определятся по формулам:
для трансформатора с заземленной нейтралью

для трансформатора с изолированной нейтралью
 ,
,
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА.
1. Найдём коэффициент  по параметрам обмотки из табл.2.1.
по параметрам обмотки из табл.2.1.

2. Построим начальное распределенное напряжение для схемы замещения обмотки трансформатора, принимая значение переменной величины x/ l = 0;0,25; 0,5; 0,75; 1,0 для выражения



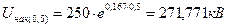


3. Построим функцию напряжения в установившемся режиме для схемы замещения согласно режима нейтрали и переменной величины x/l.
4. Рассчитаем амплитуду гармоники Аk, построим свободную составляющую распределенного напряжения Uсв1 в координатах x/l с учетом того, что если потенциалы в начале и в конце обмотки фиксированы (заземленная нейтраль), то имеем узлы высших гармоник в этих местах обмотки и целое число полуволн по всей ее длине; если потенциал фиксирован в начале обмотки и неопределен в конце (изолированная нейтраль), то имеем узел высших гармоник в начале и пучок их в конце обмотки и поэтому целое число четверть-волны напряжений по всей длине обмотки. Рассчитаем первые три гармоники для любого режима нейтрали. Проверим полученную огибающую свободной составляющей напряжения путем разности амплитуд напряжений начального распределения и установившегося
Производим расчёт совокупной составляющей распределения напряжения, условия при заземлённой изолированной нейтрали находим по формулам:
Для трансформатора с заземлённой нейтралью




Для трансформатора с изолированной нейтралью
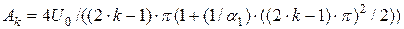



5. Построим максимальную огибающую распределенного напряжения Umax по обмотке трансформатора как сумму векторов по абсолютной величине свободной составляющей и установившейся

| 
|
6. На основании кривых огибающих минимальных потенциалов, которые удовлетворяют результатам измерений. При изолированной нейтрали наибольшее напряжение наблюдается на конце обмотки и может в 1,5-1,8 раза превышать напряжение в начале. При заземлённой нейтрали наибольшее напряжение возникает в конце первой трети обмотки и составляет (1,2-1,3)∙U0. Следовательно, в обоих случаях на главную изоляцию может воздействовать напряжение, специально превышающее напряжение источника.
Для защиты трансформатора от перенапряжения применяют:
- Экранирующие кольца.
- Компенсационные экраны.
- Увеличение продольных ёмкостей.
- Слоевые обмотки.
Литература
1. Техника высоких напряжений./ Л.Ф.Дмоховская, В.П.Ларионов, В.В.Базуткин и др.// Под ред. Д.В.Разевига. - М.: Энергия.1976, с.265-262.
2. Базуткин В.В., Ларионов В.П., Пинталь Ю.С. Техника высоких напряжений./ Под ред. В.П. Ларионова. - М.: ЭАИ.1986,с.337-347.
3. Долгинов А.И. Техника высоких напряжений в электроэнергетики. - М.: Энергия,1968. - 468 с.






