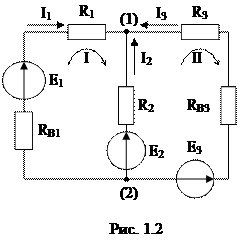
Рассмотрим на примере схемы рис. 1.2.
Общее число уравнений, записанных на основании законов Кирхгофа равно числу неизвестных токов, т.е. числу ветвей в электрической цепи.
Первый закон Кирхгофа вытекает из принципа непрерывности электрического тока, согласно которому ни в одной точке электрической цепи заряды не исчезают и не возникают: сколько зарядов к этой точке прибывает, сколько от нее и уходит. Второй закон Кирхгофа применяется к контурам электрической цепи.
Таким образом, число уравнений, составляемых по первому N1 и второму N2 законам Кирхгофа:
N1 = у- 1 = 2-1 = 1;
N2 =в-(у-1) = 3-(2-1) = 2,
где у - число узлов; в - число ветвей.
Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю:
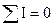 .
.
При записи все токи, подходящие к узлу, можно считать положительными, а уходящие от узла - отрицательными.
Второй закон Кирхгофа: в любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме напряжений на пассивных элементах, входящих в этот контур:
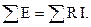
В этом уравнении положительные знаки принимаются для токов и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.
Уравнения по законам Кирхгофа:
для узла (1): I1+I2+I3=0;
для контура I: I1(RВ1+R1) -I2R2=E1-E2;
для контура II: I2R2-I3(RВ3+R3) =E2-E3.
3. Метод узловых потенциалов. В этом методе в качестве неизвестных принимают потенциалы узлов. Метод основан на первом законе Кирхгофа и законе Ома.
Один из узлов выбирают в качестве базового (т.е., потенциал этого узла считают равным нулю). Сообщить узлу нулевой потенциал можно, заземлив узел. При этом токораспределение в схеме не изменится.
На примере схемы рис.1.2, имеющей 2 узла, заземляем узел 2, тогда потенциал узла 1, умноженный на сумму проводимостей ветвей, сходящихся в этом узле, равен узловому току 1-го узла.
Узловой ток определяется алгебраической суммой токов, полученных от деления ЭДС ветвей, подходящих к узлу 1 на сопротивления данных ветвей. Если ЭДС направлена к узлу, ток принимается со знаком плюс, если от узла - со знаком минус.
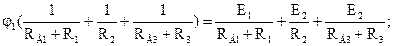
Далее определим токи в ветвях согласно закону Ома, используя вычисленный потенциал узла (1) и потенциал узла (2).
Примечание: для упрощения расчетов в схемах с числом узлов более двух, участки с последовательно-параллельным соединением пассивных элементов, можно заменить эквивалентным сопротивлением.
Закон Ома:
а) для пассивного участка (не содержащего ЭДС): ток прямо пропорционален напряжению и обратно пропорционален сопротивлению данного участка;
б) для активного участка (содержащего источник энергии):
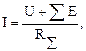
где U - напряжение между началом и концом участка, совпадающее по направлению с током;
∑E- алгебраическая сумма ЭДС, действующих на выбранном участке;
R∑-суммарное сопротивление участка.
Например, для схемы рис. 1.2 закон Ома для первой ветви:
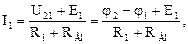
Примечание: если ЭДС совпадает по направлению с положительным направлением тока, то она записывается с положительным знаком, а если не совпадает - с отрицательным
4. Если в результате расчета какой-либо ток получится отрицательным, то это значит, что истинное направление этого тока противоположное тому, которое обозначено на схеме.






