Символы и обозначения в инженерной графике
· Обозначения точек в начертательной геометрии: А, В, С или 1,2,3
· Обозначения линий: k, l, m, n, …
· Обозначения поверхностей и плоскостей: α, β и т.д.
· Обозначения углов: ψ, ω, δ
· Обозначения плоскостей проекций: π1, π2 и т.д.
· Обозначения осей: x, y, z
Центральное и параллельное проецирование
(Рисунок 1) Центральной проекцией точек А1 и А2 называют точку А0, пересечение проецирующей прямой А0S с плоскостью проекции π0.
Каждая точка пространства имеет только одну центральную проекцию, которая не позволяет судить о положении этой точки в пространстве.
Для определения положения точки в пространстве необходимо получить две её центральные проекции из двух различных центров проекций.
Множество проецирующих прямых при заданных π0 и S образуют коническую поверхность, поэтому центральную проекцию часто называют конической. На рисунке 2 пример конической поверхности.
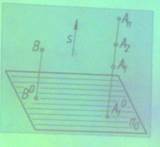Параллельное проецирование:
Рисунок 3. Способ параллельного проецирования.
Параллельной проекцией точек А1 и А2 называют точку А0, пересечение проецирующей прямой с плоскостью проекции π0 с проецирующей прямой параллельно направлению S.
Параллельная проекция является частным случаем центральной проекции, если центр проекции S удалить в бесконечность. Каждая точка имеет только одну параллельную проекцию, которая не определяет её положение в пространстве.
Для определения положения точки в пространстве необходимо получить две параллельные проекции из двух различных направлений проецирования (рисунок 4).
Множество проецирующих прямых образует цилиндрическую поверхность, поэтому параллельную проекцию часто называют симметрической (рисунок 5).
Частный случай параллельного проецирования, при котором направление S перпендикулярно плоскости проекции π0 называют прямоугольным (ортогональным).
Основные инвариантные свойства параллельного проецирования
При параллельном проецировании между оригиналом и проекцией существует определённая связь, т.е. некоторые свойства оригинала сохранятся и на проекции. Такие свойства назвали инвариантными.
Свойства:
1. Проекция прямой линии в общем случае тоже прямая линия (частные случаи: а) если направление проецирования совпадает с прямой, то проекцией будет точка; б)если прямая параллельна плоскости проекции, то она проецируется без искажений)
2. Если точка принадлежит линии, то проекция этой точки принадлежит проекции линии. Следствие: если прямые пересекаются, то точка пересечения их проекций является проекцией точки пересечения их прямых.
3. Проекции параллельных прямых тоже параллельны
4. Если отрезок делится точкой в некотором отношении, то проекция этой точки делит проекции отрезка в том же самом отношении. Следствие-1: середина отрезка проецируется в середину его проекции. Следствие-2: отношение длин параллельных отрезков равно отношению их проекций.
5. 
(ТОЛЬКО К ПРЯМОУГОЛЬНОМУ ПРОЕЦИРОВАНИЮ!)
