Статические свойства электромеханического преобразователя с независимым возбуждением
Математическое описание процессов преобразования энергии в двигателе постоянного тока с независимым возбуждением
Обмотка якоря и обмотка возбуждения двигателя постоянного тока с независимым возбуждением в общем случае получают питание от различных источников постоянного тока. Необходимым условием электромеханического преобразования энергии является протекание переменных токов по всем обмоткам машины, или хотя бы по их части. В машине постоянного тока протекание переменного тока в обмотке якоря обеспечивается коллектором, коммутирующим постоянный ток источника питания с частотой, равной электрической скорости ротора. Таким образом, двигатель постоянного тока в принципе является машиной переменного тока.
В тоже время, другим необходимым условием электромеханического преобразования энергии в двигателе является взаимная неподвижность магнитных полей статора и ротора. Так как обмотка возбуждения рассматриваемого двигателя расположена на статоре и подключена к источнику постоянного тока, ее магнитное поле неподвижно относительно статора. Следовательно, магнитное поле ротора, вращающегося со скоростью w, вращается с той же скоростью в обратную сторону, оставаясь так же неподвижным относительно статора двигателя. Таким образом, в неподвижных осях, связанных со статором, якорь представляется как обмотка, обтекаемая постоянным током iя и создающая неподвижное магнитное поле, направление которого совпадает с осью щеток двигателя. В реальной машине по этой же оси направлены также МДС обмоток дополнительных полюсов ДП и компенсационной обмотки КО.
С учетом всего вышесказанного модель двигателя постоянного тока с независимым возбуждением представлена на рис 2.1а.
Обмотки ДП и КО непосредственно в процессе электромеханического преобразования энергии не участвуют. Обмотка ДП обеспечивает вблизи оси щеток a такое магнитное поле, при котором процессы коммутации на коллекторе протекают наиболее благоприятно.
|
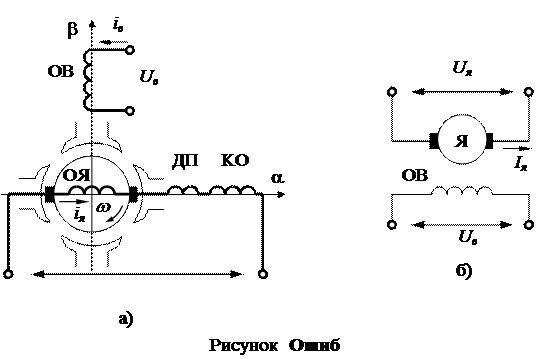
Обмотка КО обтекается током якоря и создает МДС, компенсирующую реакцию якоря по поперечной оси a. В машинах без компенсационной обмотки эта реакция якоря создает размагничивающую продольную составляющую по оси b.
Такое вспомогательное назначение обмоток ДП и КО позволяет не показывать их на принципиальной схеме включения двигателя постоянного тока, которая используется для записи уравнений электрического равновесия цепей двигателя и механической характеристики (рис. 2.1б).
Математическое описание динамического процесса преобразования энергии в двигателе с независимым возбуждением выглядит следующим образом:
|
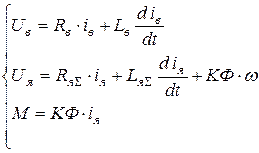 ,
,
где Lв - полная индуктивность обмотки возбуждения;
LяS - суммарная индуктивность рассеяния обмоток ОЯ, ДП и КО, т.к. основная МДС обмотки ОЯ по оси a компенсируется МДС обмотки КО;
Rв - активное сопротивление обмотки возбуждения;
RяS - активное сопротивление всех обмоток якорной цепи двигателя;
Ф - магнитный поток двигателя;
 - конструктивный коэффициент;
- конструктивный коэффициент;
pп - число пар полюсов;
N - число активных проводников обмотки якоря;
a - число параллельных ветвей обмотки якоря.
Так как уравнения системы (2.1) содержат произведения переменных, то, если в процессе работы двигателя магнитный поток изменяется, математическое описание механической характеристики двигателя постоянного тока с независимым возбуждением нелинейно. В большинстве реальных электроприводов рассматриваемый двигатель работает при постоянном магнитном потоке. В этом случае система (2.1) линеаризуется, и уравнение механической и электромеханической характеристик двигателя с независимым возбуждением запишутся в виде:
|
 ,
,
|
 .
.
Уравнение статических электромеханической и механической характеристик двигателя могут быть получены при Ф =const подставкой  :
:
|
 ,
,
|
 .
.
Из (2.4) и (2.5) следует, что при Ф =const электромеханическая и механическая характеристики двигателя с независимым возбуждением являются прямыми линиями. Эти характеристики, как и любая прямая, могут быть охарактеризованы двумя точками: точкой идеального холостого хода, в которой I =0, M =0, и точкой короткого замыкания, в которой w =0 (рис. 2.2).

Подставив в (2.4) и (2.5) I =0, M =0 получим скорость идеального холостого хода:
|
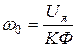 .
.
Величины тока и момента короткого замыкания Iя.кз и Mкз получим, подставив в (2.4) и (2.5) и w =0:
|
 ;
; 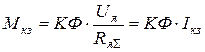 .
.
Координаты двух точек прямой полностью характеризуют ее положение на плоскости. Но при рассмотрении характеристик двигателя важно иметь показатель того, в какой степени изменяется скорость двигателя при изменении момента (нагрузки), насколько жесткая характеристика. Таким показателем электромеханических свойств двигателя является модуль статической жесткости механической характеристики bст, который может быть определен следующим образом (из уравнения (2.5)):
|
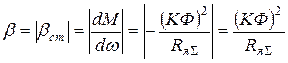 .
.
Отрицательный знак жесткости механической характеристики bст определяет ее «падающий» характер в координатах M(I), w (рис. 2.2). То обстоятельство, что и электромеханическая, и механическая характеристики двигателя являются прямыми линиями, позволяет совместить эти характеристики в координатах M(I), w, подобрав соответствующим образом масштабы M и I на оси абсцисс.
Учитывая (2.6) и (2.8) уравнения статических механической (2.5) и электромеханической (2.4) характеристик рассматриваемого двигателя могут быть записаны в следующих формах:
|
 ;
; 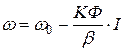 ;
;
|
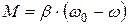 ;
;  ;
;
|
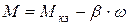 ;
;  .
.





