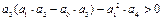Передаточные функции. Основные свойства преобразования Лапласа.
Для анализа и синтеза САУ необходимо иметь математическое описание систем. Для этой цели системы разделяются на отдельные элементы (звенья, подсистемы) и составляются уравнения, описывающие поведение этих элементов. Уравнения составляются на основании анализа физических, химических, технологических, экономических, социальных и иных процессов, происходящих в конкретных элементах. Используются соответствующие законы (закон сохранения массы, энергии, вещества и пр.), применяются специальные исследования и экспериментальные методы для получения математического описания звеньев систем.
Все математические модели (ММ) разделяются на:
1. ММ стационарных и нестационарных САУ;
-ММ САУ с распределенными и сосредоточенными параметрами;
-Статические характеристики;
Динамические ММ в виде
1. Дифференциальные уравнения;
2. Разностные уравнения (для дискретных САУ);
3. Передаточные функции (ММ в виде структурной схемы);
Временные и частотные характеристики.
Передаточная функция звена
Преобразование Лапласа имеет следующий вид 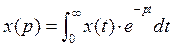 где
где 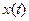 - аргумент,
- аргумент, 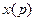 - изображение данного аргумента,
- изображение данного аргумента, 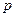 - некоторая переменная которая называется переменная Лапласа
- некоторая переменная которая называется переменная Лапласа
Свойства преобразования при начальных нулевых значениях т.е. t=0 x(t)=0
1) 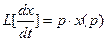 ,
, 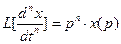 , 2)
, 2) 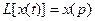 , 3)
, 3)  ,
, 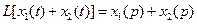 , 4)
, 4) 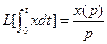 , где L-преобразование
, где L-преобразование
Преобразование по Лапласу с использованием его свойств
 возьмем отношение
возьмем отношение 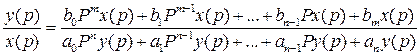
Отношение преобразуем по Лапласу выходной величины АСР или линейно к преобразованной по Лапласу входной величины элемента называется передаточной функцией АСР или элемента. Знаменатель передаточной функции = 0, называется характеристическим уравнением АСР 
Определение. Передаточной функцией звена W (S) называется отношение изображений Лапласа выходной и входной величин при нулевых начальных условиях.
Устойчивость САУ. Критерий Рауса-Гурвица
Чтобы АСР нормально работала она должна быть устойчивая. Устойчивость АСР – способность возвращаться к установившемуся положению (установленное значение регулируемой величины после прекращения действия возмущения которое вывело её из данного установившегося положения). Для оценки устойчивости работы АСР применяют
1)Алгебраичес-й критерий Гурвиц и Раус.2)Частотные критерии Найквиста и Михайлова
Критерий Гурвица –основан на анализе неравенств состоящих из коэффициентов уравнения АСР. Характеристическое уравнение n-порядка
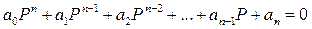
Оценка устойчивости АСР n-порядка по критерию Гурвица производится:
составляется из коэффициентов характеристического уравнения Таблица Гурвица – по главной диагонали выписываются 
 ; строка таблицы с нечетным и чётными индексами чередуются; число элементов каждой строки = n, недостающие коэффициенты заполняются нулями; отчеркивая строки и столбцы получают n определителей Гурвица. АСР n-порядка является устойчивой если все
; строка таблицы с нечетным и чётными индексами чередуются; число элементов каждой строки = n, недостающие коэффициенты заполняются нулями; отчеркивая строки и столбцы получают n определителей Гурвица. АСР n-порядка является устойчивой если все  (
(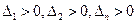 ). Устойчивость АСР оценивается по 2-м условиям 1) - Необходимо положительно всех коэффициентов характеристического уравнения
). Устойчивость АСР оценивается по 2-м условиям 1) - Необходимо положительно всех коэффициентов характеристического уравнения 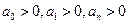 2) – Достаточным является выполнение неравенств для определённого порядка АСР
2) – Достаточным является выполнение неравенств для определённого порядка АСР
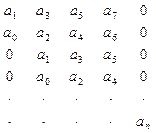
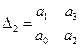


Условия получения положительного определителя Гурвица:
АСР 2-го порядка 1. 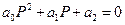 Достаточное условие устойчивости АСР является положительность коэффициентов характеристического уравнения. АСР 3-го n=3
Достаточное условие устойчивости АСР является положительность коэффициентов характеристического уравнения. АСР 3-го n=3 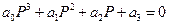 достаточное условие
достаточное условие  . АСР 4-го n=4
. АСР 4-го n=4 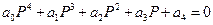 достаточное условие
достаточное условие