Функция Лейбензона.
При установившейся изотермической фильтрации сжимаемой жидкости и газа закон Дарси и вытекающие из него формулы, выведенные в предыдущем параграфе, не выполняются, так как объемный расход Q в этих законах в условиях сжимаемости возрастает по мере падения давления за счет расширения жидкости или газа. Одинаковым остается массовый расход Qm ,, что вытекает из условия сплошности и неразрывности потока:
(4.1)
Л.С. Лейбензон впервые ввел потенциальную функцию:
(4.2)
Тогда закон Дарси можно переписать, введя понятие массовой скорости фильтрации 
:
или 
, (4.3)
где 
.
Проведя такую аналогию можно сделать вывод, что все формулы полученные для установившейся фильтрации несжимаемой жидкости по закону Дарси можно использовать и для установившейся фильтрации сжимаемой жидкости и газа при тех же граничных условиях со следующей заменой переменных:
| Объемный расход Q | ® | массовый расход Qm | |
Скорость фильтрации 
| ® | массовая скорость фильтрации
| |
| Давление р | ® | функция Лейбензона 
|
Например, формула Дюпюи в условиях сжимаемости будет иметь вид:
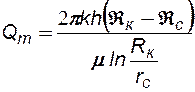(4.4)
Остается определить вид функции Лейбензона для различных сжимаемых флюидов.
1. Для сжимаемой жидкости выполняется следующее уравнение состояния, полученное из закона Гука:
(4.5)
где bж – коэффициент сжимаемости жидкости.
При 
(например, для воды bж » 4,5×10-101/Па) экспоненту можно разложить в ряд и ограничиться первыми двумя членами разложения можно приближенно записать:
(4.6)
Тогда точное значение функции Лейбензона для сжимаемой жидкости равно:
, (4.7)
а приближенное:
(4.8)
т.е. можно считать жидкость несжимаемой.
2. Для идеального газа уравнение состояния Менделеева - Клайперона при изотермическом течении можно записать так:
Þ 
(4.9)
где rат - плотность газа при атмосферном давлении и пластовой температуре.
Функция Лейбензона для идеального газа имеет вид:
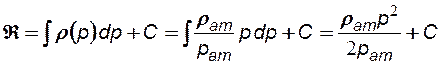(4.10)
А) Для плоско-параллельной фильтрации идеального газа массовый дебит на галерее скважин:
(4.11)
Приведенным расходом Qат назовем объемный расход, приведенный к атмосферному давлению и пластовой температуре:
(4.12)
Тогда из 4.11 получим:
(4.13)
Используя (3.3) получим распределение давления при фильтрации идеального газа, рис.5:
(4.14)
В) При плоскорадиальной фильтрации формула для приведенного дебита газовой скважины (аналог формулы Дюпюи (3.5)) будет иметь вид:
(4.15)
Индикаторную линию для газов строят в координатах 
и 
.
Используя (3.7) получим распределение давления в круговом пласте для идеального газа:
(4.16)
В случае плоскорадиальной фильтрации идеального газа по двучленному закону фильтрации приведенный дебит скважины можно определить из формулы:
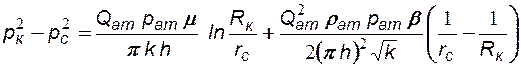(4.17)
При этом индикаторные линии газовых скважин, в призабойной зоне которых заведомо нарушается закон Дарси, строят в координатах 
, и тогда формула для обработки таких линий принимает следующий вид:
(4.18)
где: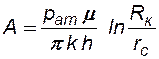 
, 
.
Задачи к разделу 4
Задача 4.1
Вывести зависимость дебита идеального газа совершенной скважины от депрессии на круговой пласт с радиусом Rк, если радиус скважины rс, вязкость μ, давление на контуре и забое pк, pс, мощность пласта h, а фильтрация происходит по закону Форшгеймера.
Задача 4.2
В пласте имеется установившаяся плоскорадиальная фильтрация идеального газа по закону Дарси. Давление на контуре питания pк = 9,8 МПа, на забое pс = 6,86 МПа, приведённый к атмосферному давлению объёмный расход газа Qат = 8∙105 м3/сут. Радиус контура питания Rк =750 м, скважины rс = 0,1 м, мощность пласта h = 10 м, пористость m = 20%. Определить давление, скорость фильтрации и истинную среднюю скорость движения газа на расстоянии r =50 м от скважины.
Задача 4.3
Определить скорость фильтрации и среднюю скорость движения при плоскорадиальной фильтрации идеального газа к совершенной скважине у ее стенки rс = 0,1м и на расстоянии r =150 м от центра скважины, если давление в этой точке равно р = 7,84МПа, мощность пласта h =12 м, его пористость m = 20%, а приведенный к атмосферному давлению и пластовой температуре дебит Qат =2×106 м3/сут.
Задача 4.4
Определить радиус призабойной зоны rкр, в которой нарушается закон Дарси, при плоскорадиальной фильтрации идеального газа, если известно, что приведенный к атмосферному давлению при пластовой температуре Qат =2·106 м3/сут, мощность пласта h = 10 м, коэффициент пористости пласта m = 19 %, коэффициент проницаемости k = 0,6 Д, динамический коэффициент вязкости газа в пластовых условиях μ =1,4×10-5кг/м×с, плотность газа при атмосферном давлении и пластовой температуре rат =0,7кг/м3.
Указание: Использовать формулу Миллионщикова и взять Reкр =0,022
Задача 4.5
Дебит газовой скважины, приведенный к атмосферному давлению при пластовой температуре Qат =2·106 м3/сут, абсолютное давление на забое рс =7,84 МПа, мощность пласта h = 10 м, коэффициент пористости пласта m = 18 %, коэффициент проницаемости k = 1,2 Д, средняя молекулярная масса газа 18 г/моль, динамический коэффициент вязкости газа в пластовых условиях μ = 0,015 мПа·с, температура пласта T= 45°С.
Определить, имеет ли место фильтрация по закону Дарси в призабойной зоне совершенной скважины радиусом rс = 0,1 м (по Щелкачёву и Миллионщикову).
Задача 4.6
Совершенная скважина расположена в центре кругового пласта радиуса Rк = 10 км, мощность пласта h = 15 м, коэффициент проницаемости k = 400 мД, вязкость жидкости μ = 1,02 мПа∙с, коэффициент сжимаемости βж = 4,64∙10-10 Па-1. Давление на контуре pк = 11,76 МПа, забойное рс =7,35 МПа, радиус скважины rс = 0,1 м. Фильтрация подчиняется закону Дарси.
Определить различие в объёмном суточном дебите скважины, подсчитанным с учётом и без учёта сжимаемости жидкости. Сделать вывод по полученным результатам.
Указание: Зависимость плотности жидкости от пластового давления считать по формуле (4.5).
Задача 4.7
Определить расстояние r от возмущающей газовой скважины до точки пласта, в которой давление равно среднеарифметическому от забойного pс =70атм и контурного pк =100 атм. Радиус контура питания Rк = 1000 м, радиус скважины rс = 10 см.
Задача 4.8
Определить объёмный, приведённый к атмосферному давлению и массовый дебиты совершенной скважины, считая, что фильтрация происходит по закону Дарси, если мощность пласта h = 25 м, проницаемость k = 250 мД, вязкость газа m = 0,014 мПа∙с, плотность газа при нормальных условиях rат = 0,650 кг/м3, радиус скважины rс = 0,1 м, расстояние до контура питания Rк = 900 м, абсолютное давление на забое скважины pс = 2,94 МПа и на контуре питания pк = 3,92 МПа. Газ считать идеальным.
Задача 4.9
Найти коэффициенты А и В уравнения (4.18) индикаторной кривой, а также коэффициент гидропроводности по данным испытания газовой скважины радиусом rс = 0,1 м, работающей в круговом пласте радиусом Rк = 1000 м.
| pк, кгс/см2 | pс, атм | Qат, тыс.м3/сут. |
| 95,3 | 94,5 | 85,52 |
| 95,3 | 210,75 | |
| 95,3 | 89,5 | 251,21 |
Задача 4.10
Построить распределение давления при стационарной фильтрации упругой жидкости (плотность при атмосферном давлении и пластовой температуре r =850кг/м3) между двумя рядами скважин с давлением рк =51атм в нагнетательном ряду и массовым расходом Qm = 50т/сут на добывающем ряду. Расстояние между рядами L = 5000м. Значения параметров пласта и жидкости следующие: k =1Д, h =10 м, bж =10-101/Па, В =1000м.
Определить давление на забоях скважин в добывающем ряду.
Сравнить результаты с фильтрацией несжимаемой жидкости при тех же условиях и сделать вывод.
Указание: Зависимость плотности жидкости от пластового давления считать по формуле (4.5).
