Задачи для самостоятельного решения. Практическое занятие №8: основные распределения дискретных случайных величин В пожарной части находятся три машины

Практическое занятие №8: основные распределения дискретных случайных величин

1. В пожарной части находятся три машины. Вероятность своевременного прибытия на пожар для каждой машины равна 0,6. а) Построить закон распределения числа машин, прибывших во время к очагу возгорания. Вычислить б) математическое ожидание и в) среднее квадратичное отклонение числа машин, своевременно прибывших на пожар.

	0.064	0.288	0.432	0.216

,

1. Игральный кубик подбрасывается 3 раза. Найти выражение для функции распределения числа выпавших двоек. Построить ее график.

	0.579	0.347	0.069	0.0046

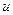
		0.579	0.926	0.995

1. Случайная величина подчинена закону Пуассона с математическим ожиданием а=3. Построить функцию распределения этой случайной величины. Найти вероятность того, что примет значение, меньшее, чем а и вероятность того, что примет положительное значение.

								…
	0.05	0.149	0.224	0.224	0.168	0.101	0.05	…

									…
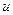
		0.05	0.199	0.423	0.647	0.815	0.916	0.966	…

1. Средняя плотность болезнетворных микробов в 1 м³ воздуха равна 100. Берется на пробу 2 дм³ воздуха. Найти вероятность того, что в нем обнаружится хотя бы один микроб.

(Ответ: )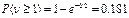

1. На ткацком станке нить обрывается в среднем 0.375 раза в течение часа. Найти вероятность того, что за смену (8 часов) число обрывов нити будет: а) не менее двух; б) не более четырех.

(Ответ: , )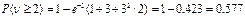

1. В автосалоне покупатели выбирают машины. Как правило, первые несколько автомобилей отвергаются, пока покупатель не найдет подходящий. Найти ряд распределения случайной величины – количества просмотренных автомобилей, если вероятность того, что покупателю понравится машина, равна 1/5. Найти среднее значение данной случайной величины.

							…
	0.2	0.16	0.128	0.102	0.082	0.066	…

 

1. В ящике 5 белых шаров и 7 черных. Наугад извлекают 2 шара. Найти дисперсию, среднее квадратичное отклонение и моду числа белых шаров среди извлеченных.

 

 

Задачи для самостоятельного решения

 

1. В некотором городе число ограблений банка представляет собой простейший поток событий с интенсивностью λ=2,5 год^-1. Сколько ограблений происходит в среднем за один год? Какова вероятность того, что в течение двух лет не будет ограблений? Какова вероятность того, что в течение полугода произойдет одно ограбление? Какова вероятность того, что в течение года произойдет хотя бы одно ограбление?

2. Три безработных выпускника вуза ищут работу. Вероятность устройства на работу каждого из них в течение месяца равна 0,7. Найти а) закон распределения числа выпускников, устроившихся на работу; б) математическое ожидание и в) среднее квадратичное отклонение числа выпускников, устроившихся на работу.

3. Средняя плотность изюминок в 1 кубическом сантиметре теста равна 0,5. Берется на пробу булочка из этого теста, объемом 10 кубических сантиметров. Найти вероятность того, что в ней будет обнаружено хотя бы три изюминки, если считать, что изюминки в тесте распределены по закону Пуассона.

4. Кубик подбрасывают до первого выпадения шестерки. Найти среднее число подбрасываний.

5. Найти дисперсию числа появлений события А в трех независимых испытаниях, если вероятности появления этого события одинаковы в каждом испытании, а среднее число появлений события в этих испытаниях равно 1.5.

6. В партии из 10 деталей имеется 8 стандартных. Наудачу отобраны две детали. Составить закон распределения числа стандартных деталей среди отобранных. Найти математическое ожидание и среднее квадратичное отклонение данной случайной величины.