ЛЕКЦІЯ № 8
Тема № 7-8. Криві та поверхні другого порядку
з навчальної дисципліни Лінійна алгебра та аналітична геометрія
напряму підготовки УПРАВЛІННЯ ІНФОРМАЦІЙНОЮ БЕЗПЕКОЮ
освітньо-кваліфікаційного рівня БАКАЛАВР
Лекція розроблена
Кандидатом фізико-математичних наук Жихарєвою Ю.І.
Навчальна та виховна мета:
1. Студенти повинні знати теоретичні питання з теми «Криві та поверхні другого порядку»: означення кривих та поверхонь другого порядку, їх види та властивості.
2. Студенти повинні вміти складати рівняння кривих та поверхонь другого порядку та будувати їх.
3.Розвиток мислення студентів, залучення до вивчення математики, як необхідної складової фахівця технічного університету
План.
1. Поняття лінії другого порядку.
2. Коло, еліпс, гіпербола, парабола. Їх властивості, канонічні рівняння.
3. Поняття поверхні другого порядку.
5. Поверхні другого порядку: сфера, еліпсоїд, гіперболоїди, параболоїди.
4. Циліндричні, конічні поверхні.
5. Поверхні обертання.
ЛІТЕРАТУРА:
1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.: ЦУЛ, 2002 – 401 с.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – Москва: Наука, – 1988 – 240 с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч 1-2. Москва.: Высшая школа, 1986.
4. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум. - К.:ЦУЛ, 2003 – 536 с.
5. Овчинніков П.Ф., Яремчик Ф.П., Михайленко В.М. Вища математика. – К.: Техніка, ч.І 596 с., ч.ІІ 792 с., 2000.
Конспект лекції
Поняття лінії другого порядку
Означення. Плоска лінія  , задана рівнянням
, задана рівнянням  , називається алгебраїчною, якщо функція
, називається алгебраїчною, якщо функція  представляється скінченним числом доданків вигляду:
представляється скінченним числом доданків вигляду:  , де
, де 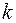 і
і  – цілі невід’ємні числа,
– цілі невід’ємні числа,  – константи. Найбільше значення суми (
– константи. Найбільше значення суми (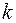 +
+  ) називається порядком алгебраїчної лінії.
) називається порядком алгебраїчної лінії.
Лінії, що не є алгебраїчними, називаються трансцендентними.
Приклад 1:
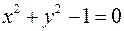 – алгебраїчна лінія другого порядку (коло одиничного радіусу з центром у початку координат).
– алгебраїчна лінія другого порядку (коло одиничного радіусу з центром у початку координат).
Приклад 2:
 – трансцендентна лінія (нескінченний ряд).
– трансцендентна лінія (нескінченний ряд).
Відповідно до означення, загальні рівняння першого і другого порядків мають вигляд:
лінії 1-го порядку:
 (1)
(1)
A і B не рівні нулю.
Це прямі лінії.
лінії 2-го порядку:
 (2)
(2)
A,B,C не рівні нулю одночасно, тобто  .
.
Еліпс, гіпербола, парабола. Їх властивості, канонічні рівняння.
Еліпс.
Означення. Еліпсом називається геометричне місце точок площини, сума відстаней яких від двох заданих точок  і
і  цієї площини (фокусів) є величина стала і більша від відстані між фокусами.
цієї площини (фокусів) є величина стала і більша від відстані між фокусами.
Канонічне рівняння еліпса
 a>0, b>0 (3)
a>0, b>0 (3)

Завжди вважатимемо, що 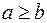 , оскільки в іншому випадку завжди можна вибрати іншу систему координат, зробивши заміну
, оскільки в іншому випадку завжди можна вибрати іншу систему координат, зробивши заміну  на
на  і
і  на
на  .
.
Нехай  – довільна точка еліпса. Позначимо
– довільна точка еліпса. Позначимо  ,
,  ,
,  . Відстані
. Відстані  називаються фокальними радіусами точки
називаються фокальними радіусами точки  .
.

Весь еліпс вміщується в прямокутнику зі сторонами 2  і 2
і 2  . Еліпс перетинає осі координат в точках
. Еліпс перетинає осі координат в точках  ,
,  ,
,  ,
,  . Ці точки називаються вершинами еліпса.
. Ці точки називаються вершинами еліпса.
Величини  ,
,  називаються відповідно великою та малою осями еліпса, а величини
називаються відповідно великою та малою осями еліпса, а величини  і
і  називають відповідно великою і малою півосями еліпса.
називають відповідно великою і малою півосями еліпса.
Позначимо відстань між фокусами 
 (фокальну відстань) через
(фокальну відстань) через 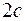 :
: 
 =
= 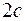 . Половина фокальної відстані
. Половина фокальної відстані  .
.
Якщо  =
=  , то рівняння (3) перетворюється на рівняння кола:
, то рівняння (3) перетворюється на рівняння кола:

Ексцентриситетом еліпса називається відношення половини фокальної відстані до довжини великої півосі еліпса. Позначається
 .
.
Директрисами еліпса називаються прямі  і
і 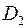 з рівняннями
з рівняннями  (- відповідає фокусу
(- відповідає фокусу  , + відповідає фокусу
, + відповідає фокусу  ).
).
Нехай  і
і  – відстані від довільної точки М еліпса відповідно до фокусу
– відстані від довільної точки М еліпса відповідно до фокусу  і директриси
і директриси  , аналогічно
, аналогічно 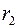 і
і 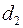 – відстані від М до
– відстані від М до  і
і 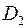 .Тоді справедлива рівність:
.Тоді справедлива рівність:

2) Гіпербола.
Означення. Гіперболою називається геометричне місце всіх точок площини, абсолютна величина різниці відстаней яких від двох заданих точок  і
і  цієї площини (фокусів) є величина стала і менша від відстані між фокусами.
цієї площини (фокусів) є величина стала і менша від відстані між фокусами.
Канонічне рівняння гіперболи
 (4)
(4)
a>0, b>0
Нехай  – довільна точка гіперболи. Позначимо
– довільна точка гіперболи. Позначимо  ,
,  ,
,  . Відстані
. Відстані  називаються фокальними радіусами точки
називаються фокальними радіусами точки  .
.
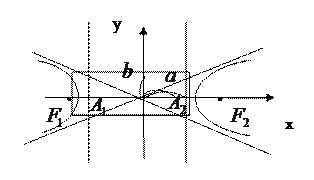
Вся гіпербола складається з двох віток (лівої і правої), має дві асимптоти  і розташована поза прямокутником зі сторонами 2
і розташована поза прямокутником зі сторонами 2  і 2
і 2  , який називається основним. Гіпербола перетинає вісь
, який називається основним. Гіпербола перетинає вісь  в точках
в точках  ,
,  ,які називаються вершинами гіперболи. Вісь
,які називаються вершинами гіперболи. Вісь  гіпербола не перетинає.
гіпербола не перетинає.
Величини  ,
,  називаються відповідно дійсною та уявною осями гіперболи, а величини
називаються відповідно дійсною та уявною осями гіперболи, а величини  і
і  називаються відповідно дійсною та уявною півосями гіперболи.
називаються відповідно дійсною та уявною півосями гіперболи.
Якщо  =
=  , то рівняння перетворюється на рівняння:
, то рівняння перетворюється на рівняння: 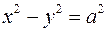 ,
,
яке визначає рівносторонню гіперболу, основним прямокутником якої є квадрат із стороною 2  , а асимптотами – прямі
, а асимптотами – прямі  .
.
Рівняння  або
або 
також визначає гіперболу з вершинами  ,
,  і тими ж асимптотами. Гіперболи
і тими ж асимптотами. Гіперболи 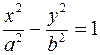 і
і  називаються спряженими.
називаються спряженими.
Ексцентриситетом гіперболи називається відношення половини фокальної відстані до довжини дійної півосі еліпса. Позначається
 .
.
Оскільки  , то
, то  . Крім того, з формули
. Крім того, з формули  дістаємо, що
дістаємо, що
 .
.
Директрисами гіперболи називаються прямі  і
і 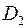 з рівняннями
з рівняннями  (- відповідає фокусу
(- відповідає фокусу  , + відповідає фокусу
, + відповідає фокусу  ). Вони мають ту ж властивість, що й директриси еліпса:
). Вони мають ту ж властивість, що й директриси еліпса: 
3) Парабола.
Означення. Параболою називається геометричне місце всіх точок площини, рівновіддалених від заданої точки 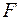 цієї площини (фокуса) і від заданої прямої
цієї площини (фокуса) і від заданої прямої 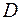 (директриси), яка не проходить через фокус.
(директриси), яка не проходить через фокус.
Канонічне рівняння параболи
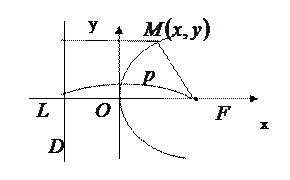
 (5)
(5)
Нехай  – довільна точка параболи. Позначимо
– довільна точка параболи. Позначимо  ,
, 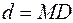 ,
,  .
.
Число  називається параметром параболи.
називається параметром параболи.  .
.
Парабола перетинає вісь  в точці
в точці  , яка називається іі вершиною. Вісь симетрії
, яка називається іі вершиною. Вісь симетрії  параболи називається її віссю.
параболи називається її віссю.
Параметр  впливає на форму параболи. Із збільшенням параметра
впливає на форму параболи. Із збільшенням параметра  парабола розширюється від осі
парабола розширюється від осі  .
.
Якщо r і d - відстані точки еліпса (гіперболи) до фокусу і до директриси, що відповідає цьому фокусу, то відношення  (еліпса(гіперболи)), то аналогічно:
(еліпса(гіперболи)), то аналогічно:
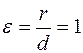 (параболи).
(параболи).
Рівняння  ,
,  ,
,  , в яких
, в яких  теж визначають параболи
теж визначають параболи

Директриса параболи має рівняння. 
Поняття поверхні другого порядку
Означення. Поверхня  , задана рівнянням
, задана рівнянням 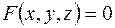 , називається алгебраїчною, якщо функція
, називається алгебраїчною, якщо функція  представляється скінченним числом доданків вигляду:
представляється скінченним числом доданків вигляду: 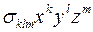 , де
, де 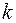 ,
,  і
і  – цілі невід’ємні числа,
– цілі невід’ємні числа,  – константи. Найбільше значення суми (
– константи. Найбільше значення суми (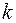 +
+  +
+  ) називається порядком алгебраїчної поверхні.
) називається порядком алгебраїчної поверхні.
Лінії, що не є алгебраїчними, називаються трансцендентними.
Відповідно до цього означення, загальні рівняння поверхонь першого і другого порядків мають вигляд:
лінії 1-го порядку: 
з цього виходить:

A, B, C не рівні нулю одночасно.
Це площини.
лінії 2-го порядку:
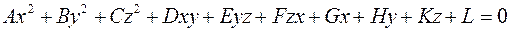
Тут перші шість коефіцієнтів не рівні нулю одночасно.
4. Найважливіші невироджені поверхні 2-го порядку:






