1. Дослідимо систему на сумісність, для чого визначимо ранг матриці системи. У випадку сумісності:
2. Визначимо число вільних і базисних невідомих.
3. Виразимо базисні невідомі через вільні. Для цього застосуємо метод
Гаусса до матриці системи.
4. Знаходимо загальний розв’язок системи.
Приклад 1. Дослідити на сумісність, у випадку сумісності знайти розв’язки однорідної системи лінійних алгебраїчних рівнянь.
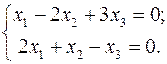
Розв’язання. 1) Дослідимо систему на сумісність, для чого визначимо ранг матриці системи:
~ 
,
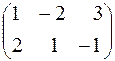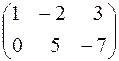
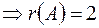
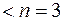отже система сумісна.
2) Визначимо число вільних і базисних невідомих.
, 
, 
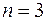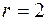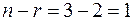– є одне вільне невідоме, наприклад, 
.
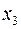Невідомі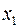 
і 
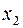– базисні.
3) Виразимо базисні невідомі через вільні. Для цього застосуємо метод Гаусса до матриці системи:
~ 
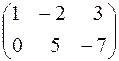, звідки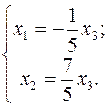 
4) Знаходимо загальний розв’язок системи. Вільним невідомим можна надавати будь-яких значень. Нехай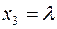 
, де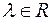 
. Тоді
, 
.
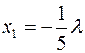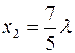Загальний розв’язок: , , ,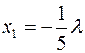
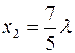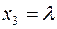Загальний розв’язок можна також записати у вигляді матриці-рядка
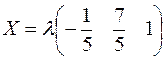, де .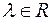
Відповідь: 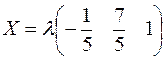, де .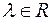
Дослідження систем лінійних алгебраїчних рівнянь на сумісність.
Теорема Кронекера-Капеллі.
Розглянемо довільну систему лінійних алгебраїчних рівнянь
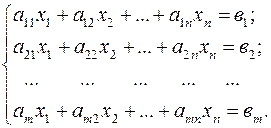(1)
Складемо з коефіцієнтів цієї системи основну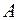 
і розширену 
матрицю:
, 
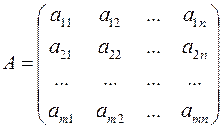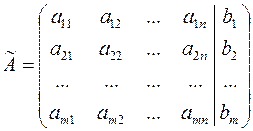
Наступна теорема дає повну відповідь на запитання про сумісність системи (1), тобто про існування її розв’язку.
Теорема Кронекера-Капеллі. (Леопольд Кронекер (1823-1891) – німецький математик, Альфред Капеллі (185-1910) – італійський математик). Система лінійних алгебраїчних рівнянь сумісна тоді і тільки тоді, коли ранг основної матриці системи дорівнює рангу розширеної матриці системи.
СЛАР сумісна.
Як тільки з’ясовано, сумісна дана система лінійних алгебраїчних рівнянь чи ні, виникає питання про її визначеність або невизначеність, тобто єдиний розв’язок має система або безліч розв’язків.
Теорема (про число розв’язків системи) 1. Якщо ранг основної матриці системи дорівнює рангу розширеної матриці системи і дорівнює числу невідомих, то система визначена, тобто має єдиний розв’язок.
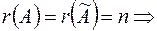СЛАР визначена (має єдиний розв’язок)
2. Якщо ранг основної матриці системи дорівнює рангу розширеної матриці системи, але менше числа невідомих, то система невизначена, тобто має розв’язків.
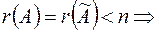СЛАР невизначена (має безліч розв’язків)
Як тільки з’ясовано число розв’язків даної сумісної системи лінійних алгебраїчних рівнянь, виникає питання знаходження цих розв’язків.
Замінимо в неоднорідній системі (1) всі вільні члени нулями. Отримана таким чином система лінійних алгебраїчних рівнянь називається однорідною системою асоційованою з даною (або зведеною системою).
Теорема. (про структуру розв’язків неоднорідної СЛАР). Загальний розв’язок неоднорідної системи лінійних алгебраїчних рівнянь дорівнює сумі деякого частинного розв’язку цієї системи і загального розв’язку однорідної системою асоційованої з даною.
ЗР НСЛАР = ЧР+ ЗР ОСЛАР
З теорем випливає наступна
