Погружение ДИ
Шаг 1. Матрица  размера
размера  контейнера разбивается стандартным образом на
контейнера разбивается стандартным образом на  блоки;
блоки;  — произвольный блок.
— произвольный блок.
Шаг 2. В каждый блок  погружается очередной бит
погружается очередной бит  ДИ:
ДИ:
2.1. Для  строится нормальное сингулярное разложение:
строится нормальное сингулярное разложение:  ;
;  и
и  — левый и правый СНВ блока
— левый и правый СНВ блока  соответственно, отвечающие максимальному СНЧ
соответственно, отвечающие максимальному СНЧ  , определяемые однозначно.
, определяемые однозначно.
2.2. (погружение  ):
):
Если  ,
,
то
2.2.1.  , где
, где  — возмущенный в ходе СП
— возмущенный в ходе СП  ;
;
2.2.2. Определение  ,...,
,...,  — возмущенных
— возмущенных  в процессе приведения левых сингулярных векторов к ортонормированному с
в процессе приведения левых сингулярных векторов к ортонормированному с  виду путем решения системы линейных алгебраических уравнений относительно элементов
виду путем решения системы линейных алгебраических уравнений относительно элементов  ,...,
,...,  ;
;
иначе
2.2.1.  , где
, где  — возмущенный в ходе СП
— возмущенный в ходе СП  ;
;
2.2.2. Вычисление  ,...,
,...,  — возмущенных
— возмущенных  в процессе приведения правых сингулярных векторов к ортонормированному с
в процессе приведения правых сингулярных векторов к ортонормированному с  виду путем решения системы линейных алгебраических уравнений относительно элементов
виду путем решения системы линейных алгебраических уравнений относительно элементов  ,...,
,...,  .
.
2.3. (формирование блока  СС, отвечающего блоку
СС, отвечающего блоку  контейнера).
контейнера).
Если  ,
,
то  , где
, где 
 ,...,
,..., 
иначе  , где
, где 
 ,...,
,...,  .
.
Декодирование ДИ.
Шаг 1. Матрица СС  размера
размера  разбивается стандартным образом на
разбивается стандартным образом на  блоки;
блоки;  — произвольный блок.
— произвольный блок.
Шаг 2. Из каждого блока  извлекается очередной бит
извлекается очередной бит  ДИ:
ДИ:
2.1. Для  строится нормальное сингулярное разложение:
строится нормальное сингулярное разложение:  ;
;  и
и  — левый и правый СНВ блока
— левый и правый СНВ блока  соответственно, отвечающие максимальному СНЧ
соответственно, отвечающие максимальному СНЧ  , определяемые однозначно.
, определяемые однозначно.
2.2. (извлечение  ). Найти
). Найти  и
и  — углы между векторами
— углы между векторами  ,
,  и
и  ,
,  соответственно.
соответственно.
Если 
 , то
, то  ,
,
иначе  .
.
Организация действий шага 2.2.2 при погружении ДИ проводится в разработанном алгоритме следующим образом (рассмотрим на примере матрицы  (рис.1), где
(рис.1), где  — вектор-столбец, ортогональный векторам
— вектор-столбец, ортогональный векторам  и
и 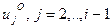 ). Обеспечение ортогональности левых СНВ достигается путем решения системы из 28 линейных алгебраических уравнений с неизвестными
). Обеспечение ортогональности левых СНВ достигается путем решения системы из 28 линейных алгебраических уравнений с неизвестными  — элементами векторов
— элементами векторов  (рис.1):
(рис.1):
 (3.2)
(3.2)
где  — скалярное произведение векторов-аргуметов. Матрица
— скалярное произведение векторов-аргуметов. Матрица  , фигурирующая при формировании матрицы
, фигурирующая при формировании матрицы  блока СС на шаге 2.3 при погружении дополнительной информации, включает в себя нормализованные векторы-столбцы
блока СС на шаге 2.3 при погружении дополнительной информации, включает в себя нормализованные векторы-столбцы 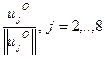 :
:
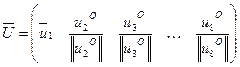

 ,...,
,...,  .
.
 При организации погружения ДИ на шаге 2.2 возмущение матрицы блока в большинстве случаев не приводило к нарушению надежности восприятия (рис.2) (за исключением случаев, оговоренных ниже), поскольку возмущение
При организации погружения ДИ на шаге 2.2 возмущение матрицы блока в большинстве случаев не приводило к нарушению надежности восприятия (рис.2) (за исключением случаев, оговоренных ниже), поскольку возмущение  ,
,  при их приравнивании к
при их приравнивании к  в подавляющем большинстве блоков незначительно.
в подавляющем большинстве блоков незначительно.
Для проверки эффективности разработанного стеганоалгоритма  в среде MATLAB был проведен вычислительный эксперимент, в ходе которого ЦИ размером
в среде MATLAB был проведен вычислительный эксперимент, в ходе которого ЦИ размером  пикселя подвергались стеганопреобразованию при помощи алгоритма
пикселя подвергались стеганопреобразованию при помощи алгоритма  . Полученные стеганосообщения сохранялись первоначально в формате TIF, после чего производилось декодирование дополнительной информации. Затем СС пересохранялись в формат JPEG с разными коэффициентами качества. Результаты эксперимента для 300 изображений, подтверждающие устойчивость
. Полученные стеганосообщения сохранялись первоначально в формате TIF, после чего производилось декодирование дополнительной информации. Затем СС пересохранялись в формат JPEG с разными коэффициентами качества. Результаты эксперимента для 300 изображений, подтверждающие устойчивость  к атакам сжатием, в том числе с низким коэффициентом качества, приведены в таблице 3.2. Здесь В качестве количественной оценки устойчивости стеганоалгоритма к возмущающим воздействиям используется коэффициент корреляции
к атакам сжатием, в том числе с низким коэффициентом качества, приведены в таблице 3.2. Здесь В качестве количественной оценки устойчивости стеганоалгоритма к возмущающим воздействиям используется коэффициент корреляции  для декодированной ДИ, который определяется в соответствии с формулой:
для декодированной ДИ, который определяется в соответствии с формулой:
 ,
,
где  ,
,  ― ДИ, погруженная в контейнер;
― ДИ, погруженная в контейнер;  ,
,  ― декодированная ДИ;
― декодированная ДИ;
 , если
, если  ;
;  , если
, если  .
.


а б
Рис.2. Иллюстрация результата стеганопреобразования при помощи алгоритма  : ЦИ-контейнер (формат TIF) (а); б – СС (формат TIF) (б)
: ЦИ-контейнер (формат TIF) (а); б – СС (формат TIF) (б)
Таблица 3.2
Результаты декодирования ДИ стеганоалгоритмом 
| Формат СС | TIF | JPEG | |||

| 
| 
| 
| ||
Среднее значение 
| 0.9603 | 0.9577 | 0.9498 | 0.9454 | 0.9359 |
Необходимо отметить, что основным возмущающим воздействием для получаемого при помощи  стеганосообщения, как свидетельствуют результаты эксперимента (табл.3.2), является не процесс сжатия, а процессы округлений, происходящие после стеганопреобразования, связанные с введением значений элементов
стеганосообщения, как свидетельствуют результаты эксперимента (табл.3.2), является не процесс сжатия, а процессы округлений, происходящие после стеганопреобразования, связанные с введением значений элементов  (
( ) в диапазон целых значений от 0 до 255, за счет которых и происходят наибольшие из наблюдаемых возмущения углов между
) в диапазон целых значений от 0 до 255, за счет которых и происходят наибольшие из наблюдаемых возмущения углов между  ,
,  и
и  ,
,  , приводящие к ошибкам при декодировании ДИ. В последующем процессе сжатия дальнейшее уменьшение
, приводящие к ошибкам при декодировании ДИ. В последующем процессе сжатия дальнейшее уменьшение  практически не происходит. Для более полной иллюстрации в таблице 3.3 приведены примеры нескольких ЦИ.
практически не происходит. Для более полной иллюстрации в таблице 3.3 приведены примеры нескольких ЦИ.
Таблица 3.3






