В.Г. Кульков
ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ
МЕТАЛЛА И ПОЛУПРОВОДНИКА
Методические указания к выполнению лабораторной работы № 1
по курсу «Электротехническое материаловедение»
Волжский, 2016
УДК 620.22
Рецензент:
Поляков А.С. – канд. физ.-мат. наук, доцент
филиала ФГБОУВО «НИУ «МЭИ» в г. Волжском
Температурная зависимость сопротивления металла и полупроводника: Методические указания к выполнению лабораторной работы № 1 по курсу «Электротехническое материаловедение» / Сост.В.Г. Кульков. – Волжский: Филиал МЭИ в г. Волжском, 2014. – 9 с.
В ходе выполнения работы измеряется зависимость сопротивления металла и полупроводника от температуры. По результатам этих измерений вычисляется температурный коэффициент сопротивления металла и энергия активации проводимости полупроводника.
Работа предназначена для студентов очной (дневной), очно-заочной (вечерней) и заочной форм обучения по направлениям 130301 «Теплоэнергетика и теплотехника» и 130302 «Электроэнергетика и электротехника».
Печатаются по решению Учебно-методического совета филиала МЭИ в г. Волжском.
УДК 620.22
© Филиал МЭИ в г. Волжском, 2016
ЦЕЛЬ РАБОТЫ
Целью работы является овладение методикой экспериментального нахождения зависимости сопротивления электротехнических материалов от температуры и расчет связанных с этим физических величин.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Температурная зависимость сопротивления металов
Квантовая теория проводимости приводит к следующему выражению для удельного сопротивления металлов
. (1)
Из этого выражения видно, что зависимость удельной проводимости или сопротивления от температуры может быть обусловлена только соответствующей зависимостью длины свободного пробега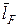 
.
Электрическое сопротивление току обусловлено различного рода процессами рассеяния электронов на дефектах. Идеальный металлический кристалл не рассеивает электронов по той причине, что он не содержит дефектов. На основе корпускулярно-волнового дуализма можно считать электроны в кристалле волнами. Длина таких волн составляет 3 – 7 Å. Таким образом, движение электронов в металле представляет собой распространение волн в периодической структуре. Квантовая механика приводит к результату, заключающемуся в том, что в такой системе рассеяния не происходит. Это означает, что сопротивление должно обратиться в нуль. Однако, в реальности это не так.
В случае чистых металлов, не содержащих примеси и структурных дефектов, рассеяние электронов происходит только на динамических дефектах кристаллической решетки. Ими являются тепловые колебания атомов, центры которых расположены в узлах решетки. Под действием температуры эти атомы совершают колебания, отклоняясь от своих положений равновесия, подобно маятникам. При этом максимальная упругая энергия достигается при максимальных отклонениях 
и равна средней тепловой энергии колебаний, приходящейся на одну степень свободы.
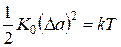. (2)
Здесь K 0 – постоянная, характеризующая упругую связь атома в решетке.
Пусть поток электронов поперечного сечения 
попадает нормально на плоскую поверхность. Считаем, что колеблющийся атом аналогичен рассеивающему центру с площадью, равной площади круга радиуса . Тогда вероятность испытать рассеяние одному электрону в рассматриваемой ситуации равна
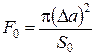. (3)
Продвижение на глубину 
увеличивает вероятность рассеяния пропорционально числу атомов в рассматриваемом объеме:
, (4)
где N – число атомов в единице объема. Далее учтем, что средняя длина свободного пробега электронов 
обратно пропорциональна вероятности их рассеяния на единице длины пробега.
. (5)
Отсюда с учетом (2.72) получаем
. (6)
Такая формула для средней длины пробега электронов приводит к зависимости удельного электрического сопротивления металлов от температуры, если учесть (2.64)
. (7)
Из (7) видно, что удельное сопротивление растет прямо пропорционально температуре. Это происходит в достаточно широком интервале температур, примерно от 
почти до температуры плавления. Здесь 
– температура Дебая, ωmax – максимальная частота колебаний атомов в решетке. При температурах, не сильно далеких от комнатных, используется формула 
, где ρ0 – удельное сопротивление при t =0ºC, а αρ – температурный коэффициент удельного сопротивления.
