Обучение многослойных нейронных сетей прямого распространения методом обратного распространения ошибки.

Рассмотрим процесс обучения нейронной сети с использованием алгоритма обратного распространения ошибки (backpropagation).

Чтобы обучить нейронную сеть мы должны подготовить обучающие данные (примеры). В нашем случае, тренировочные данные состоят из входных сигналов (х₁ и х₂) и желаемого результата z.

Обучение – это последовательность итераций (повторений).
В каждой итерации весовые коэффициенты нейронов подгоняются с использованием новых данных из тренировочных примеров.
Изменение весовых коэффициентов и составляют суть алгоритма, описанного ниже.

Каждый шаг обучения начинается с воздействия входных сигналов из тренировочных примеров. После этого мы можем определить значения выходных сигналов для всех нейронов в каждом слое сети.
Иллюстрации ниже показывают, как сигнал распространяется по сети.
Символы W(Xm)n представляют вес связи между сетевым входом Xm и нейрона n во входном слое.

Символы y(n) представляют выходной сигнал нейрона n.

Распространение сигнала через скрытый слой.
Символы Wmn представляют весовые множители связей между выходом нейрона m и входом нейрона n в следующем слое.

Распространение сигнала через выходной слой:

На следующем шаге алгоритма, выходной сигнала сети y сравнивается с желаемым выходным сигналом z, который хранится в тренировочных данных. Разница между этими двумя сигналами называется ошибкой d выходного слоя сети:

Невозможно непосредственно вычислить сигнал ошибки для внутренних нейронов, потому что выходные значения этих нейронов, неизвестны.
На протяжении многих лет был неизвестен эффективный метод для обучения многослойной сети.

Только в середине восьмидесятых годов был разработан алгоритм обратного распространения ошибки.

Идея заключается в распространении сигнала ошибки d (вычисленного в шаге обучения) обратно на все нейроны, чьи выходные сигналы были входящими для последнего нейрона.

Весовые коэффициенты Wmn, используемые для обратного распространения ошибки, равны тем же коэффициентам, что использовались во время вычисления выходного сигнала. Только изменяется направление потока данных (сигналы передаются от выхода ко входу).
Этот процесс повторяется для всех слоёв сети. Если ошибка пришла от нескольких нейронов — она суммируются:

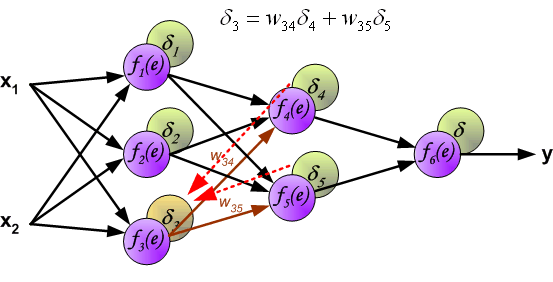
Когда вычисляется величина ошибки сигнала для каждого нейрона – можно скорректировать весовые коэффициенты каждого узла ввода(дендрита) нейрона.
В формулах ниже df(e)/de — является производной от функции активации нейрона (чьи весовые коэффициенты корректируются).

Вычисление производной необходимо, потому что для корректировки весовых коэффициентов при обучении ИНС с помощью алгоритма обратного распространения, используется метод градиентного спуска.

Данные итерации повторяются до тех пор, пока точность работы нейронной сети на обучающей выборке не будет соответствовать заданному уровню (или же до тех пор, пока точность работы нейронной сети в процессе обучения не перестанет увеличиваться)

Задание на практическую работу:

1. Взять готовые исходные данные и сгенерировать свои собственные данные. Использовать эти данные для обучения однослойной нейронной сети методом дельта-правила. Провести нормировку исходных данных. Построить график применяемой функции активации нейронов. Привести в отчете пример 10 итераций по обучению нейронной сети. Построить график изменения средней квадратической погрешности Гаусса в зависимости от номера итерации обучения. В отчете привести конечные значения весовых коэффициентов и схему нейронной сети.

2. Взять готовые исходные данные и сгенерировать свои собственные данные. Использовать эти данные для обучения многослойной нейронной сети методом обратного распространения ошибки. Привести в отчете пример 10 итераций по обучению нейронной сети. Построить график изменения средней квадратической погрешности Гаусса в зависимости от номера итерации обучения. В отчете привести конечные значения весовых коэффициентов и схему нейронной сети.

3. Взять готовые исходные данные и сгенерировать свои собственные данные. Использовать эти данные для настройки нейронной сети Хэмминга. В отчете привести матрицу весовых коэффициентов первого слоя настроенной нейронной сети. Подать на вход не менее 10 зашумленных сигналов. Для каждого входного сигнала определить значение выходных сигналов нейронной сети, количество итераций потребовавшихся для анализа входного сигнала. Сделать вывод о возможности использования этих характеристик в качестве критерия достоверности при решения задач классификации с помощью нейронной сети Хэмминга.

Исходные данные для выполнения пункта практического задания представлены в таблице 1. P ₁… P ₉ – входные сигналы, Class – выходной сигнал (при выполнении задания по рекуррентной нейронной сети), I и F – выходные сигналы (при выполнении заданий про нейронные сети прямого распространения)

Таблица 1 – Исходные данные для обучения нейронных сетей (зеленым показаны входные данные, синим - выходные)

№	P ₁	P ₂	P₃	P ₄	P ₅	P ₆	P ₇	P ₈	P ₉	Class	I	F
	61,83917	85,40581			32,53909	16,67908				C1	5,68
		74,67025	65,60821	65,60821	65,60821	65,60821	21,34831	10,94284		C1	5,67
	83,82353	17,59962	83,82353					17,59962		C1	5,71
	87,5063	66,32242		66,32242	59,01763	59,01763	17,0529	8,740554		C1	6,15
	62,17237	93,74262		68,66588	93,74262	62,17237	15,98583	8,193625		C1	6,2
	93,18416	58,7963	93,18416		65,86934	51,33745	51,33745	8,487654		C1	6,2
	76,26662	71,37981		80,9558	76,26662	42,13079	36,56126	30,72224		C1	6,53
		84,51589	80,30303	80,30303	51,66297	46,84035	11,73319	6,005174		C1	6,6
	94,50069				64,33502	58,3295	14,61114	7,478141		C1	6,59
	74,75682	94,61447			63,84342	58,03084	14,13998	7,236062		C2	7,08
	88,9917				63,84342	20,71174	7,236062			C2	7,04
	94,85722	83,9904		83,9904	62,35785	36,40384	29,22669	4,334091		C2	7,09
				75,18224	45,80848	36,945	5,301524			C2	7,44
	80,55303	97,20888		60,78151	50,59068	25,79514	21,64092		12,7353	C2	7,34
	93,74789				75,74992	47,47219	13,83552	4,819683		C2	7,43
	93,19464		82,19075	79,8471	58,92969	37,22271	11,27961	3,922797		C3	7,94
	84,35646		88,48851	70,73039	49,77883	27,44633	21,11339	17,73654		C3	7,85
	68,23958		76,36203	54,28224	32,82131	27,25163	6,774229	3,458946		C3	7,94
		95,29426	95,29426	78,55338	39,55951	28,5955	6,908172	3,526297		C4	8,36
	93,33677			63,57778	36,73154	30,6225	7,397861	3,77626		C4	8,34
	84,14986		88,18444	70,29483	49,32387	27,08934	20,98204	17,73443		C4	8,29
	94,93372		85,75686	54,7734	30,53129	25,21837	22,39235	6,381667		C5	8,68
	93,77787		86,8922	53,71478	29,79441	24,92114	5,863157			C5	8,81
	83,87897		76,76816	17,28548	14,87067	14,87067	14,87067	14,87067		C5	8,89
	89,31014		22,02759	17,78044	17,78044	17,78044	17,78044	17,78044		C6	9,25
	93,96382		83,67997	60,5921	55,09112	13,08854	10,82582	10,82582		C6	9,22
		95,51199	81,99821	50,9802	42,89979	25,92298	20,8976	5,761767		C6	9,08
	93,37507	65,59729		65,59729	58,68545	16,24935	8,320292			C1	6,05
		81,20035	76,52251	76,52251	47,80229	42,43601	36,80494	6,443071		C1	6,1
	92,97229	59,01763	92,97229		59,01763	51,3602	43,32494	43,32494		C1	6,07
		50,86048	64,42774	68,62155	68,62155	42,35589	10,60986			C1	6,54
	80,7889	93,88848		61,72389	55,10105	48,13733	7,913319			C1	6,52
	93,88848			61,72389	55,10105	48,13733	48,13733	7,913319		C1	6,57
	65,0494	94,0944			65,0494	58,66081	15,41164	7,881449		C1	6,98
	94,0944				65,0494	58,66081	15,41164	7,881449		C2	7,07
	88,55857	96,35224		75,5102	67,42729	41,84477	37,16857	5,511811		C2	7,1
	96,69978			76,27363	68,9843	44,2967	10,04486			C3	7,62
	81,4167	97,33284		65,50056	56,17169	32,89914	25,12095	4,441136		C3	7,59
	76,54159		86,10601	83,06219	62,8444	34,79402	26,56783	4,69693		C2	7,49
	71,30264	92,32778		75,31832	46,01698	36,84296	10,67581			C3	7,9
	76,71669		87,85812	69,39518	47,7035	42,22374	21,48704	18,22419		C4	8,12
	91,74936		86,16345	68,05664	46,78336	24,1387	17,87267	17,87267		C4	8,1
	86,05111		86,05111	61,55163	35,59009	28,63541	8,047945			C4	8,44
	83,5353		86,05111	61,55163	35,59009	28,63541	8,047945			C4	8,41
	77,1996	95,42484		64,00201	37,07893	11,27451	3,921569			C4	8,46
	88,58437		92,06774	69,02109	18,99138	5,340166				C6	9,06
	85,78199		80,68118	9,261788	12,60342	12,60342	12,60342		10,16146	C6	9,25
		94,7327	83,15093	69,97087	8,652862	2,629714				C6	9,24
		92,1159		6,390386	6,390386	6,390386	6,390386	6,390386	6,390386	C7	9,62
	93,16534		10,15994	19,37637	19,37637	19,37637	2,63491			C7	9,64
	97,96775		90,99363	15,9655	2,55718	11,86352	2,55718			C7	9,59
	90,72778		1,927318							C7	9,98
		87,75323	75,43766	62,34997	5,863466					C7	10,17
		95,74453	76,03687	62,11838	27,90899	17,35311	4,485887			C7	10,04
		82,8667	51,04294	42,3536	25,61071	21,88511	6,503067	2,253207		C7	10,54
		90,11834	56,32548	48,78614	46,71221	29,88898	8,100525	2,805905		C7	10,41
		68,81205	17,46793	19,91076	19,91076	19,91076	19,91076	4,417178		C7	10,57
		76,61274	33,39136	36,36084	22,71145	19,49621	5,621544	1,945525		C7	11,01
		78,81811	45,67482	37,8248	36,07061	21,21478	17,27881	15,1957		C7	10,91