Обозначим через k произведение нескольких (больше одного) первых простых чисел. Докажите, что число
а) k – 1; б) k + 1 не является точным квадратом.
5. Пусть a и n – натуральные числа, большие 1. Докажите, что если число an – 1 простое, то a = 2 и n – простое.
(Числа вида q = 2n – 1 называются числами Мерсенна.)
Сумма двух натуральных чисел равна 201. Докажите, что произведение этих чисел не может делиться на 201
7. Целые числа x, y и z таковы, что (x – y)(y – z)(z – x) = x + y + z. Докажите, что число x + y + z делится на 27.
8. Докажите, что среди любых десяти последовательных натуральных чисел найдётся число, взаимно простое с остальными.
9. Натуральное число n назовём суперсоставным, если каждый его простой делитель меньше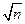 
. Докажите, что существует бесконечно много троек последовательных суперсоставных чисел.
10. Наименьший нечётный делитель натурального числа n, отличный от 1, равен d, а наибольший нечётный делитель n равен числу D > d. Оказалось, что n = 3D+5d. Найдите все такие n.
11. Найдите все пары простых чисел p и q (p > q) такие, что (p+q)3 не делится на 3, но делится на (p–q)2.
12*. У натурального числа n выписали четыре различных делителя, меньших n, оканчивающихся на одну и ту же ненулевую цифру. Докажите, что их сумма меньше, чем 6n/7.
15 декабря 2016 Делимость и остатки, простые числа
1. а) p, p + 10, p + 14 – простые числа. Найдите p. б) p, 2p + 1, 4p + 1 – простые числа. Найдите p
2. p и p2 + 2 – простые числа. Докажите, что p3 + 2 – также простое число.
3. Решить в целых числах уравнение xy + 3x - 5y = 32
Обозначим через k произведение нескольких (больше одного) первых простых чисел. Докажите, что число
а) k – 1; б) k + 1 не является точным квадратом.
5. Пусть a и n – натуральные числа, большие 1. Докажите, что если число an – 1 простое, то a = 2 и n – простое.
(Числа вида q = 2n – 1 называются числами Мерсенна.)
Сумма двух натуральных чисел равна 201. Докажите, что произведение этих чисел не может делиться на 201
7. Целые числа x, y и z таковы, что (x – y)(y – z)(z – x) = x + y + z. Докажите, что число x + y + z делится на 27.
8. Докажите, что среди любых десяти последовательных натуральных чисел найдётся число, взаимно простое с остальными.
9. Натуральное число n назовём суперсоставным, если каждый его простой делитель меньше 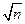. Докажите, что существует бесконечно много троек последовательных суперсоставных чисел.
10. Наименьший нечётный делитель натурального числа n, отличный от 1, равен d, а наибольший нечётный делитель n равен числу D > d. Оказалось, что n = 3D+5d. Найдите все такие n.
11. Найдите все пары простых чисел p и q (p > q) такие, что (p+q)3 не делится на 3, но делится на (p–q)2.
12*. У натурального числа n выписали четыре различных делителя, меньших n, оканчивающихся на одну и ту же ненулевую цифру. Докажите, что их сумма меньше, чем 6n/7.
15 декабря 2016 Делимость и остатки, простые числа
1. а) p, p + 10, p + 14 – простые числа. Найдите p. б) p, 2p + 1, 4p + 1 – простые числа. Найдите p
2. p и p2 + 2 – простые числа. Докажите, что p3 + 2 – также простое число.
3. Решить в целых числах уравнение xy + 3x - 5y = 32
