2012.
Интегральные характеристики систем заряженных частиц
Полный заряд системы 
Замечание. Механическая аналогия: заряд – аналог массы, плотность заряда – аналог плотности массы. Аналогия особенно понятна, если речь идет о зарядах одного знака.
Закон сохранения заряда
Обоснования закона сохранения заряда.
1.Электрон и протон являются материальными частицами с бесконечным временем жизни; их элементарные электрические заряды инвариантны и не зависят от скорости. В этом аспекте закон сохранения заряда является просто следствием неуничтожимости носителей заряда как физических объектов и инвариантности заряда.
2. Кроме протонов и электронов существует большое число других заряженных элементарных частиц. Все они порождаются, порождают другие частицы и уничтожаются в различных процессах взаимопревращений. Каков бы ни был процесс взаимопревращения частиц, суммарный заряд частиц до взаимопревращения равен суммарному заряду частиц после взаимопревращения. Заряд сохраняется при всех процессах и движениях, связанных с носителями зарядов.
Закон сохранения заряда установлен опытным путем.
Полный заряд замкнутой24 системы, т.е. алгебраическая сумма зарядов всех входящих в систему тел, во времени не изменяется:
|
Этот закон выполняется даже тогда, когда (внутри системы) происходит рождение или уничтожение элементарных частиц25 [2, с.197].
В неизолированной системе изменение заряда определяется только токами, текущими из системы или в систему. Поэтому изменение величины заряда Q в любом объеме V пространства в единицу времени равно по величине и противоположно по знаку силе тока 
через поверхность S, ограничивающую объем V. Математическая формула закона сохранения имеет вид26 [9, с.30]:
или
| (1) |
Знак минус учитывает, что если положительный заряд внутри замкнутого объема уменьшается, то плотность тока направлена из объема наружу27.
Дифференциальная формулировка закона сохранения заряда
Будем полагать, что к интегралу в правой части (1) может быть применена теорема Остроградского-Гаусса (ее условия строго сформулируем позднее; они выполняются в большинстве физически реальных ситуаций). Тогда
.
Положение и форма объема 
не меняются во времени. Поэтому производную по времени в левой части равенства можно внести под знак интеграла. При этом полную производную следует заменить частной. Действительно, 
, при этом положение точки наблюдения 
не зависит от 
. Имеем:
(2)
Так как - произвольный объем, интегральное равенство (2) эквивалентно дифференциальному равенству:
или 
(3)
Соотношение (3) называется уравнением непрерывности тока зарядов, оно выражает закон сохранения заряда в каждой точке пространства.
Закон сохранения заряда в форме (3) имеет следующий смысл: суммарная плотность положительных и отрицательных зарядов
изменяется только за счет их прихода или ухода из объема . По отдельности положительные и отрицательные заряды не производятся в каких-либо точках пространства и соответственно не уничтожаются.
При стационарном распределении зарядов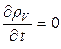 
и 
, т.е. имеет место движение зарядов лишь с замкнутыми линиями плотности тока. В случае точечных зарядов траектории движения являются замкнутыми кривыми. Более подробно поговорим об этом в теме «Элементы векторного анализа».
Электрический (дипольный) момент системы зарядов определяется интегралом
, (4)
где 
и 
- заряд и радиус-вектор элементарных частиц, находящихся в объеме 
в момент времени 
.
Замечание 1. Формула (4) определяет электрический момент относительно начала координат. Электрический момент относительно точки 
:
.
Замечание 2. Обычно мы считаем, что объемная плотность заряда 
определена во всем пространстве. Если в некоторой области нет зарядов, то в этой области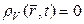 
. Поэтому определение электрического момента системы зарядов (относительно начала координат) в общем случае имеет вид
. (4+)
Позднее мы увидим, что формула (4+) годится и для случая точечных зарядов.
Для простейшей электрически нейтральной системы, состоящей из двух точечных зарядов 
и 
эта величина равна
,
где 
- вектор, направленный от отрицательного заряда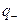 
к положительному 
.
Рис. 1
Диполь. Система двух одинаковых по величине, но противоположных по знаку зарядов называется диполем или биполем (двухполюсной системой), а 
- плечом диполя. При этом заряды не обязательно являются точечными, и если они не точечные, 
и 
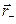- радиус-векторы электрических центров зарядов, образующих диполь (см формулу (4++)).
Важно: суммарный заряд системы 
, основной характеристикой системы является электрический момент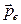 
.
Электрический момент системы зарядов часто называют дипольным моментом.
Отметим, что для электрически нейтральной системы зарядов, находящихся в объеме ,
(функция 
знакопеременная).
Упражнение. Показать, что при выполнении условия 
величина 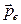не зависит от выбора начала координат.
Точечный диполь. Пусть размеры заряженных тел, образующих диполь, и расстояние между ними (плечо диполя) малы по сравнению с расстоянием от точки наблюдения до центра диполя. (Другими словами, последнее расстояние так велико, что в условиях рассматриваемой задачи два противоположных заряда можно считать слившимися в одну точку.) В этом случае диполь называется точечным.
Точечному диполю приближенно соответствует следующее распределение зарядов: два точечных заряда, одинаковых по величине и противоположных по знаку, расстояние между которыми стремится к нулю при сохранении дипольного момента 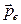постоянным. Пример такой системы зарядов изображен на рисунке 2. Здесь 
.
Рис. 2.
Переходя здесь к пределу при 
, получим точечный диполь с электрическим моментом 
, расположенный в точке с радиус-вектором 
.
Замечание 3. Если система зарядов содержит заряды одного знака, то электрический момент позволяет найти радиус-вектор центра распределения заряда (электрического центра системы зарядов):
. (4++)
(Аналогия с центром масс в механике).
Если система содержит заряды разных знаков, то находят 
(для положительных зарядов), 
(для отрицательных зарядов).
Магнитный момент системы зарядов, движущихся в объеме (объемно-распределенных токов), определяется интегралом:
, (5)
где , 
, - заряд, скорость и радиус-вектор элементарных частиц, находящихся в объеме в момент времени .
--------------------------------------------------------------------------------------------------------------------
