СОДЕРЖАНИЕ
Лабораторная работа №1. 2
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 3
Лабораторная работа №2. 4
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 5
Лабораторная работа №3. 6
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 7
Лабораторная работа №4. 8
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 9
Лабораторная работа №5. 10
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 11
Лабораторная работа №6. 12
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 13
Лабораторная работа №7. 14
Лабораторная работа №7. 14
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 15
Лабораторная работа №8. 16
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 17
Лабораторная работа №9. 18
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ.. 18
Приложение 1. Алгоритм и его свойства. 19
Приложение 2. Стандартные встроенные математические функции. 26
Приложение 3. Основные сведения об операторах VBA.. 27
Приложение 4. ПРОЦЕДУРЫ И ФУНКЦИИ В ЯЗЫКЕ VBA.. 30
Приложение 5 МАССИВЫ.. 33
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ... 35
Лабораторная работа №1
Тема: Составление и отладка линейной программы
Задание Составить программу для вычисления значения следующей функции. Ввод данных осуществить с помощью операторов присваивания. Предусмотреть вывод результатов и исходных данных. Результаты округлить до 3 знаков в дробной части.
Варианты заданий:
В.1  при а=1,25; b=-2,49; c=8,62; d=0,7; k=-0.93; x=0,38
В.2
при а=1,25; b=-2,49; c=8,62; d=0,7; k=-0.93; x=0,38
В.2 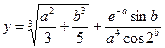 при a=-1,73; b=0,8;
В.3
при a=-1,73; b=0,8;
В.3  при a=2,3; b=4,53; c=8,26; x=0,35;
В.4
при a=2,3; b=4,53; c=8,26; x=0,35;
В.4   при a=4,72; b=5,07; x=0,21;
В.5
при a=4,72; b=5,07; x=0,21;
В.5  при a=1,68; x=0,53;
В.6
при a=1,68; x=0,53;
В.6  при a=0,45; b=7,34; x=1,27;
В.7
при a=0,45; b=7,34; x=1,27;
В.7  при a=0,83; b=1,03; c=3,76; d=0,27; x=0,95;
В.8
при a=0,83; b=1,03; c=3,76; d=0,27; x=0,95;
В.8  при a=12,145;
при a=12,145;  ; ;
| В.9  при x=0,553;
В.10
при x=0,553;
В.10  при k=3; x=0,268;
В.11
при k=3; x=0,268;
В.11  при a=-4; x=0,3
В.12
при a=-4; x=0,3
В.12  при
при  В.13
В.13  при
при  В.14
В.14  при
при  В.15
В.15  при Z=-2,538; x=1,6
при Z=-2,538; x=1,6
|
[;fgbd
fbjОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №1
Тема: Составление и отладка линейной программы
1. ПОСТАНОВКА ЗАДАЧИ
Составить программу для вычисления значения следующей функции:

при Z=-2,538; x=1,6
2 БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ
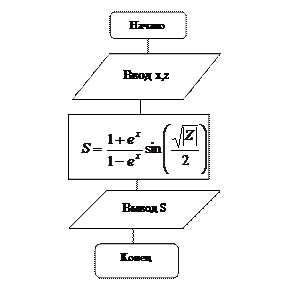
ТЕКСТ ПРОГРАММЫ
Sub lab1()
' ЛИНЕЙНЫЕ ПРОГРАММЫ
' вариант7, гр.7106, Иванов И.И.
z = -2.538: X = 1.6
S = ((1 + Exp(X)) / (1 - Exp(X))) * Sin(Sqr(Abs(z)) / 2)
S = Round(S, 3)
Debug.Print "при Z="; z, "x="; X, "S="; S
End Sub
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
при Z=-2,538; x=1,6 S = -1.077
Лабораторная работа №2
Тема: Программирование разветвляющихся алгоритмов
Задание Разработать схему разветвляющегося алгоритма и составить программу для вычисления функции. Исходные данные вводить с клавиатуры.
Получить результаты по ветви «да» и ветви «нет».
Варианты заданий:
В.1  В.2
В.2  В.3
В.3  В.4
В.4  В.5
В.5 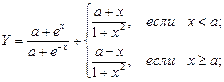 В.6
В.6  В.7
В.7 
| В.8  В.9
В.9  В.10
В.10  В.11
В.11  В.12
В.12  В.13
В.13 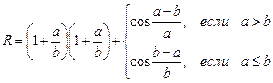 В.14
В.14  В.15
В.15 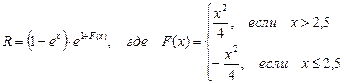
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №2
Тема: Программирование разветвляющихся алгоритмов
Составление и отладка линейной программы
1. ПОСТАНОВКА ЗАДАЧИ
Составить программу для вычисления значения следующей функции, заданной следующим образом:

2 БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ
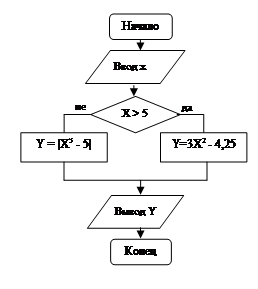 |
ТЕКСТ ПРОГРАММЫ
Sub lab2()
Rem вычисление значения функции по условию
X = InputBox("Введите x-")
X=val(x)
If X > 5 Then
Debug.Print "Условие ДА"
y = 3 * X ^ 2 - 4.25
Else
Debug.Print " Условие НЕТ"
y = Abs(3 * X ^ 3 - 5)
End If
Debug.Print "X="; X, "Y="; Y
End Sub
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Условие ДА
X=6 Y= 103,75
Условие НЕТ
X=2 Y= 19
Лабораторная работа №3
Тема: Программирование циклических алгоритмов
Задание Разработать схему циклического алгоритма и составить программу для вычисления значений функции (табулирование функции). Результаты оформить в виде таблицы.
Варианты заданий:
В.1  В.2
В.2  В.3
В.3  В.4
В.4  В.5
В.5  В.6
В.6  В.7
В.7  В.8
В.8  В.9
В.9  В.10
В.10 
| В.11  В.12
В.12  В.13
В.13  В.14
В.14  В.15
В.15  В.16
В.16  В.17
В.17 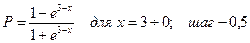 В.18
В.18  В.19
В.19  В.20
В.20 
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №3
Тема: Программирование циклических алгоритмов
1. ПОСТАНОВКА ЗАДАЧИ
Вычислить значение функции y=f(x) некоторой переменной X, изменяющейся от начального значения X0 до конечного Xk с постоянным шагом h.
Использовать значения X0=-2, Xk=2, h=0,4 для функции y=X2-4X-2.
 |
2 БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ
ТЕКСТ ПРОГРАММЫ
Sub lab3()
' циклическое вычисление функции
X0 = -2: Xk = 2: h = 0.4
For X = X0 To Xk Step h
y = X ^ 2 - 4 * X - 2
y = Round(y, 3)
Debug.Print "X="; X, "Y="; y
Next X
End Sub
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
X=-2 Y= 10
X=-1,6 Y= 6,96
X=-1,2 Y= 4,24
X=-0,8 Y= 1,84
X=-0,4 Y=-0,24
X=0 Y=-2
X= 0,4 Y=-3,44
X= 0,8 Y=-4,56
X= 1,2 Y=-5,36
X= 1,6 Y=-5,84
X= 2 Y=-6
Лабораторная работа №4
Тема: Программирование циклических алгоритмов с неизвестным числом повторений
Задание Разработать алгоритм и составить программу для вычисления корня уравнения вида f(x)=0 методом итераций при начальном приближении Х0 и заданной точности Е.
Примечание:
Рассмотрим задачу вида: решить уравнение f(x)=0, где f(x) – определена и непрерывна на [a,b]
X0 – корень уравнения, если f(X0)=0
Если уравнение содержит коэффициенты известные лишь приблизительно, то корень уравнения точно определить нельзя, но разработаны численные методы, которые позволяют отыскать приблизительные значения корней такого уравнения.
При этом уравнение решается в два этапа:
I этап – отыскание достаточно малых областей, в каждой из которых заключен один и только один корень уравнения.
II этап - вычисление корней с заданной точностью.
Пусть надо найти корни уравнения
I этап.
Воспользуемся аксиомой: если на концах некоторого отрезка непрерывная функция f(x) принимает значения разных знаков, то на этом отрезке уравнение f(x)=0 имеет хотя бы один корень.
Определим отрезок, на котором находится положительный корень уравнения
x2-2x-4=0
а) метод подстановок
| X | -1 | |||
| F(x) | -1 | -4 | -5 | +8 |
Смена знака
Следовательно, отрезок на котором находится корень –[1,2]
II этап.
Один из способов численного решения уравнений – метод итераций.
Пусть дано уравнение f(X)=0, где f(X) – непрерывная функция. Определим корни уравнения. Заменим f(X)=0 равносильным уравнением x= Ф(x). Выберем на отрезке [a,b] произвольную точку x0 нулевое приближение, и примем в качестве следующего приближения x1=Ф(x0); x2= Ф(x1) и так далее xn= Ф(xn-1). Процесс итерации продолжается до тех пор, пока выполняется неравенство |x-x0|<=e, где e – заданная точность вычисления.
Определение: процесс последовательного вычисления чисел xn по формуле xn= Ф(xn-1) называется методом итераций.
Пример: Найти корень уравнения x3-x-1=0 с точностью e=10-4.
1. Отделим корень, т.е. отыщем достаточно малую область, в которой заключен только один корень, т.е. найдем отрезок [a,b], на концах которого функция имеет разные знаки: a=1;b=1,5.
2. Преобразуем уравнение к виду x3=x+1=0 →x=(x+1)1/3. Применим метод итераций. За нулевое приближение примем x0=1.
Варианты заданий:
В.1 x – sin x - 0,25 = 0; E= 0,0004 x0=1.1
В.2 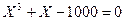 ; E = 10-4 X0 = -4
В.3 X – COS X = 0; E= 0,001 X0=0
В.4 X – 2+SIN(1/X) = 0; E= 0,0001 X0=1.2
В.5 LN(X+2.5)-X= 0; E= 0,0001 X0=2
В.6 e-x – x=0 E= 10-6 X0=0.5
В.7 -X-ARCTG(X)+6.65= 0; E= 10-5 X0=5
В.8 X3+X-1= 0; E= 10-6 X0=0.9
В.9 X – 2 + SIN(X/2) = 0; E= 0,001 X0=0
В.10 Ln(X2+1.2)-X= 0; E= 0,0001 X0=1.5 ; E = 10-4 X0 = -4
В.3 X – COS X = 0; E= 0,001 X0=0
В.4 X – 2+SIN(1/X) = 0; E= 0,0001 X0=1.2
В.5 LN(X+2.5)-X= 0; E= 0,0001 X0=2
В.6 e-x – x=0 E= 10-6 X0=0.5
В.7 -X-ARCTG(X)+6.65= 0; E= 10-5 X0=5
В.8 X3+X-1= 0; E= 10-6 X0=0.9
В.9 X – 2 + SIN(X/2) = 0; E= 0,001 X0=0
В.10 Ln(X2+1.2)-X= 0; E= 0,0001 X0=1.5
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №4
Тема: Программирование циклических алгоритмов с неизвестным числом повторений
1. ПОСТАНОВКА ЗАДАЧИ
Составить программу для вычисления корня уравнения вида f(x)=0 методом последовательных приближений (методом итераций) при начальном приближении Х0 и заданной точности Е.
Пример: Найти корень уравнения x3 –x -1 = 0 c точностью. е=10-4
2. БЛОК-СХЕМА АЛГОРИТМА РЕШЕНИЯ УРАВНЕНИЯ МЕТОДОМ ИТЕРАЦИЙ
 |
3. Текст программы
Sub lab4()
' вычисление корня уравнения методом итераций
E = 0.0001
X0 = 1
X = (X0 + 1) ^ (1 / 3)
While Abs(X - X0) > E
X0 = X
X = (X0 + 1) ^ (1 / 3)
Debug.Print "X="; X
Wend
Debug.Print
F = X ^ 3 - X - 1
Debug.Print "корень = "; X
Debug.Print "F= "; F
End
End Sub
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
X= 1,31229383668329
X= 1,32235381913882
X= 1,32426874455158
X= 1,32463262525092
X= 1,32470174851036
корень = 1,32470174851036
F= -6,91232594380864E-05
Лабораторная работа №5
Тема: Программирование сложных циклических алгоритмов
Задание Разработать алгоритм и составить программу для вычисления заданной функции.
Варианты заданий:
В.1  при изменении Х от 2 до 7 с шагом 0.5; b=5.4
В.2 при изменении Х от 2 до 7 с шагом 0.5; b=5.4
В.2 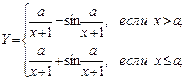 при изменении Х от 3 до 8 с шагом 0.5; a=6
В.3 при изменении Х от 3 до 8 с шагом 0.5; a=6
В.3  для Х=-1, -3, -4, 1, 2, 5
В.4 для Х=-1, -3, -4, 1, 2, 5
В.4  для Х=0.1; 0.5; 1; 1.2; 1.8; 2 а=3; b=2
В.5 для Х=0.1; 0.5; 1; 1.2; 1.8; 2 а=3; b=2
В.5  при изменении Х от -1 до 4 с шагом 0.75; при изменении Х от -1 до 4 с шагом 0.75;
|
В.6  при изменении Х от -1 до 4 с шагом 0.75;
В.7 при изменении Х от -1 до 4 с шагом 0.75;
В.7  для a=0.1; 0.5; 1.2; 1.8; 2 b=0.9
В.8 для a=0.1; 0.5; 1.2; 1.8; 2 b=0.9
В.8  при изменении Х от -1 до 4 с шагом 0.75
B.9 при изменении Х от -1 до 4 с шагом 0.75
B.9 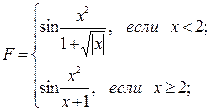 для X=0.8; 1.2; 1.9; 2.4; 3
B.10 для X=0.8; 1.2; 1.9; 2.4; 3
B.10  для X= -1; -0.5; 0.5; 1; 2.4; 4; 6 для X= -1; -0.5; 0.5; 1; 2.4; 4; 6
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №5
Тема: Программирование сложных циклических алгоритмов
1. ПОСТАНОВКА ЗАДАЧИ
Разработать алгоритм и составить программу для вычисления заданной функции
 при изменении Х от 4 до 8 с шагом 0.5
при изменении Х от 4 до 8 с шагом 0.5
 2. БЛОК-СХЕМА АЛГОРИТМА
2. БЛОК-СХЕМА АЛГОРИТМА
3. Текст программы
Sub Lab5()
FOR X = 4 TO 8 STEP 0.5
IF X>=5 THEN
Y=X+Sin(X/2)
ELSE
Y=X-Sin(X/2)
END IF
DEBUG.PRINT “X=”;X,”Y=”;Y
NEXT X
End Sub
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
X= 4 Y= 3,09070257317432
X= 4,5 Y= 3,72192680311208
X= 5 Y= 5,59847214410396
X= 5,5 Y= 5,88166099205233
X= 6 Y= 6,14112000805987
X= 6,5 Y= 6,39180486546989
X= 7 Y= 6,64921677231038
X= 7,5 Y= 6,92843868125766
X= 8 Y= 7,24319750469207
bfbfbf
Лабораторная работа №6
Тема: Использование процедур SUB при решении задач
Задание Составить программу для вычисления значения суммы или интеграла. Вычисление суммы (интеграла) оформить в виде процедуры SUB.
Варианты заданий:
В.1  В.2
В.2  В.3
В.3  В.4
В.4  В.5
В.5  В.6
В.6  В.7
В.7  В.8
В.8 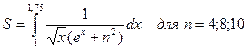 В.9
В.9 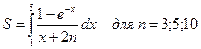
| В.10  В.11
В.11  В.12
В.12 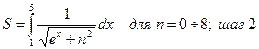 В.13
В.13  В.14
В.14  В.15
В.15  В.16
В.16  В.17
В.17 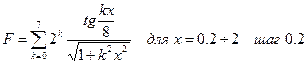 В.18
В.18 
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №6
Тема: Использование процедур SUB при решении задач
1. ПОСТАНОВКА ЗАДАЧИ
Составить программу для вычисления значения суммы или интеграла. Вычисление суммы (интеграла) оформить в виде процедуры SUB.
 |
 n=1¸3
n=1¸3
2. БЛОК-СХЕМА АЛГОРИТМА
Вычисление сумм оформим в виде процедур-SUB.
3. Текст программы
SUB Lab6()
REM пример использования процедуры-SUB
FOR n=1 TO 3
Integral(n)
NEXT n
END SUB
SUB integral(n)
B = 1.5: A=0
H = (B-A)/1000
S=0
FOR t=A TO B STEP H
S = S + (EXP(t)*(1+SIN(t)))/(1+COS(t)*n)*H
NEXT t
DEBUG.PRINT “n=”; n, “s=”;s
END SUB
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
n= 1 s= 4,16923301628827
n= 2 s= 3,27157585300758
n= 3 s= 2,72177268868186
Лабораторная работа №7
Тема: Использование процедур FUNCTION при решении задач
Задание Составить программу для вычисления значения суммы или интеграла. Вычисление суммы (интеграла) оформить в виде процедуры FUNCTION.
Варианты заданий:
В.1  В.2
В.2  В.3
В.3 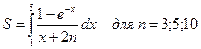 В.4
В.4  В.5
В.5  В.6
В.6 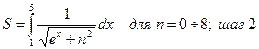 В.7
В.7  В.8
В.8  В.9
В.9 
| В.10  В.11
В.11 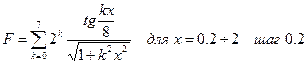 В.12
В.12 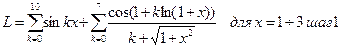 В.13
В.13  В.14
В.14  В.15
В.15  В.16
В.16  В.17
В.17  В.18
В.18 
|
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №7
Тема: Использование процедур FUNCTION при решении задач
1. ПОСТАНОВКА ЗАДАЧИ
Составить программу для вычисления значения суммы или интеграла. Вычисление суммы (интеграла) оформить в виде процедуры FUNCTION.

 X=1¸7
X=1¸7
2. БЛОК-СХЕМА АЛГОРИТМА
|
Вычисление сумм оформим в виде процедур-функций.
3. Текст программы
SUB Lab7()
REM пример использования процедуры-функции
FOR X=1 TO 7
U = SUM1(X) + SUM2(X)
DEBUG.PRINT “X=”; X, “U=”;U
NEXT X
END SUB
FUNCTION SUM1(X)
S=0
FOR K=0 TO 5
S = S + SIN(X)/(1+k)
NEXT K
SUM1 = S
END FUNCTION
FUNCTION SUM2(X)
S=0
FOR K=0 TO 4
S = S + SQR(k*X)
NEXT K
SUM2 = S
END FUNCTION
4. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
X= 1 U= 8,20786828272132
X= 2 U= 10,9199091256254
X= 3 U= 10,9913861852365
X= 4 U= 10,4383626263795
X= 5 U= 11,3941004659505
X= 6 U= 14,3706435600192
X= 7 U= 17,8711041817846
Лабораторная работа №8
Тема: Использование массивов при решении задач
Задание. Написать программу ввода числовых данных в одномерный массив, обработки этого массива и вывода результата.
Варианты заданий:
| 1. В массиве из 10 положительных и отрицательных чисел найти наименьшее положительное число и его место в массиве. 2. В массиве из 10 положительных и отрицательных чисел найти наибольшее отрицательное число и его место в массиве. 3. В массиве из 10 целых чисел каждое четное число умножить на 2. 4. В массиве из 10 целых чисел каждое нечетное число обнулить. 5. В массиве из 10 целых чисел найти числа, попадающие в указанный с клавиатуры диапазон [a;b]. Вывести эти числа на экран и подсчитать их количество. 6. В массиве из 10 целых чисел найти сумму чисел, попадающих в указанный с клавиатуры диапазон [a;b]. Вывести эти числа на экран и подсчитать их количество. 7. В массиве из 10 положительных и отрицательных чисел найти сумму всех отрицательных и сумму всех положительных чисел. 8. В массиве из 10 целых чисел найти сумму всех четных чисел. 9. В массиве из 10 целых чисел найти произведение всех нечетных чисел. 10. В массиве из 10 целых чисел найти произведение суммы четных и суммы нечетных чисел. 11. В массиве из 10 целых положительных и отрицательных чисел найти произведение суммы положительных и суммы отрицательных чисел. 12. В массиве из 10 целых чисел каждое четное число умножить на самого себя. 13. В массиве из 10 целых чисел каждое отрицательное число сделать положительным. 14. В массиве из 10 целых чисел второе четное число умножить на 100. 15. В массиве из 10 целых чисел каждое нечетное число умножить на последнее четное. 16. В массиве из 10 целых чисел найти сумму первого четного и последнего нечетного числа. 17. В массиве из 10 положительных и отрицательных чисел найти сумму первого отрицательного и последнего положительного числа. 18. В массиве из 10 положительных и отрицательных чисел каждое положительное число сделать отрицательным, а каждое отрицательное число - положительным. 19. В массиве из 10 целых чисел сделать каждое четное число нечетным, добавив к ним по единице. 20. В массиве из 10 целых чисел найти частное от деления суммы четных чисел на сумму из нечетных чисел. |
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №8
Тема: Использование массивов при решении задач
1. ПОСТАНОВКА ЗАДАЧИ
В массиве из 10 положительных чисел найти максимальное число и его положение в массиве.
2. Текст программы
Sub m_VvodDannih()
Dim m(1 To 10) As Integer
Randomize Timer
For i = 1 To 10
m(i) = Int(Rnd() * 100) + 1
Next i
Debug.Print "Исходный массив"
For i = 1 To 10
Debug.Print m(i);
Next i: Debug.Print: Debug.Print
Call obrabotka(m())
End Sub
Sub obrabotka(m1() As Integer)
Max = m1(1): k = 1
For j = 2 To 10
If m1(j) > Max Then
Max = m1(j)
k = j
End If
Next j
‘ Вывод результата
Debug.Print "max="; Max, "k="; k
End Sub
3. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Исходный массив
4 40 7 77 71 19 60 71 51 15
max= 77 k= 4
Лабораторная работа №9
Тема: Файлы последовательного доступа.
Задание. Составить программу для записи данных в файл последовательного доступа на диске с данными о сотрудниках: Фамилия, Год рождения, Оклад. Составить программу для чтения данных из файла последовательного доступа на диске содержащего данные о сотрудниках.
ОБРАЗЕЦ ОФОРМЛЕНИЯ ОТЧЕТА ПО ЛАБОРАТОРНОЙ РАБОТЕ
Лабораторная работа №9
Тема: Файлы последовательного доступа.
1. ПОСТАНОВКА ЗАДАЧИ
Составить программу для записи данных в файл последовательного доступа на диске. Составить программу для чтения данных из файла последовательного доступа на диске.
2. Текст программы
Sub запись()
номер = FreeFile
Open "d:\file1.txt" For Output As номер
n = InputBox("Количество сотрудников")
For i = 1 To n
fio$ = InputBox("Фамилия")
god% = InputBox("Год рождения")
oklad = InputBox("Оклад")
Write #номер, fio$, god%, oklad
Next i
Close номер
End Sub
Sub открытие()
номер = FreeFile
Open "d:\file1.txt" For Input As номер
n = 10000
Debug.Print "Фамилия", "Год рождения", "Оклад"
For i = 1 To n
If EOF(номер) Then Exit For
Input #номер, fio$, god%, oklad
Debug.Print fio$, god%, oklad
Next i
Close номер
End Sub
Приложение 1. Алгоритм и его свойства
Алгоритмом называется точная инструкция исполнителю в понятной для него форме, определяющая процесс достижения поставленной цели на основе имеющихся исходных данных за конечное число шагов.
Основными свойствами алгоритмов являются:
1. Универсальность (массовость) - применимость алгоритма к различным наборам исходных данных.
2. Дискретность - процесс решения задачи по алгоритму разбит на отдельные действия.
3. Однозначность - правила и порядок выполнения действий алгоритма имеют единственное толкование.
4. Конечность - каждое из действий и весь алгоритм в целом обязательно завершаются.
5. Результативность - по завершении выполнения алгоритма обязательно получается конечный результат.
6. Выполнимость - результата алгоритма достигается за конечное число шагов.
Алгоритм считается правильным, если его выполнение дает правильный результат. Соответственно алгоритм содержит ошибки, если можно указать такие допустимые исходные данные или условия, при которых выполнение алгоритма либо не завершится вообще, либо не будет получено никаких результатов, либо полученные результаты окажутся неправильными.
Выделяют три крупных класса алгоритмов:
- вычислительные алгоритмы, работающие со сравнительно простыми видами данных, такими как числа и матрицы, хотя сам процесс вычисления может быть долгим и сложным;
- информационные алгоритмы, представляющие собой набор сравнительно простых процедур, работающих с большими объемами информации (алгоритмы баз данных);
- управляющие алгоритмы, генерирующие различные управляющие воздействия на основе данных, полученных от внешних процессов, которыми алгоритмы управляют.
Способы записи алгоритмов
Для записи алгоритмов используют самые разнообразные средства. Выбор средства определяется типом исполняемого алгоритма. Выделяют следующие основные способы записи алгоритмов:
- вербальный, когда алгоритм описывается на человеческом языке;
- символьный, когда алгоритм описывается с помощью набора символов;
- графический, когда алгоритм описывается с помощью набора графических изображений.
Общепринятыми способами записи являются графическая запись с помощью блок-схем и символьная запись с помощью какого-либо алгоритмического языка.
Описание алгоритма с помощью блок схем осуществляется рисованием последовательности геометрических фигур, каждая из которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Написание алгоритмов с помощью блок-схем регламентируется ГОСТом. Внешний вид основных блоков, применяемых при написании блок схем, приведен на рисунке:
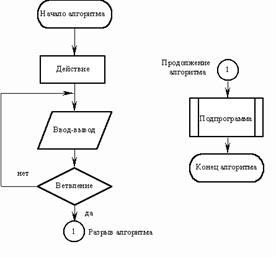
В зависимости от последовательности выполнения действий в алгоритме выделяют алгоритмы линейной, разветвленной и циклической структуры.
В алгоритмах линейной структуры действия выполняются последовательно одно за другим:

В алгоритмах разветвленной структуры в зависимости от выполнения или невыполнения какого-либо условия производятся различные последовательности действий. Каждая такая последовательность действий называется ветвью алгоритма.

Алгоритмы разветвленной структуры:
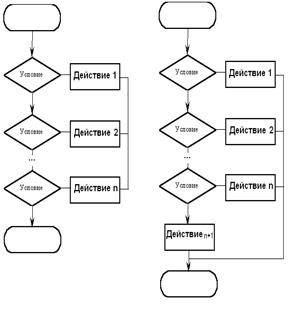 - если – то;
- если – то;
- если – то – иначе;
- выбор;
- выбор – иначе;
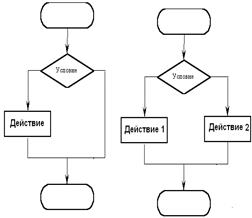
В алгоритмах циклической структуры в зависимости от выполнения или невыполнения какого-либо условия выполняется повторяющаяся последовательность действий, называющаяся телом цикла. Вложенным называется цикл, находящийся внутри тела другого цикла. Различают циклы с предусловием, послеусловием и со счетчиком:


Итерационным называется цикл, число повторений которого не задается, а определяется в ходе выполнения цикла. В этом случае одно повторение цикла называется итерацией.
Языки программирования
На практике в качестве исполнителей алгоритмов используются специальные автоматы - компьютеры. Для того, чтобы ЭВМ могла выполнять программу, программа должна быть записана по строгим правилам в виде, доступном для обработки на ЭВМ. Программа для такой машины записывается на так называемом машинном языке, т. е. представляет собой последовательность двоичных чисел. Придумывать и записывать программу на машинном языке неудобно. Это нудная и долгая работа не обходилась без ошибок, которые было очень непросто найти.
Поэтому возникла идея записывать программу на так называемом алгоритмическом языке или языке программирования. Языки программирования – специально разработанные искусственные языки, предназначенные исключительно для записи алгоритмов, исполнение которых поручается ЭВМ.
Основные понятия. Алфавит. Синтаксис. Семантика
Обычный разговорный язык состоит из четырех основных элементов: символов, слов, словосочетаний и предложений. Алгоритмический язык содержит подобные элементы, только слова называют элементарными конструкциями, словосочетания - выражениями, предложения - операторами. Алгоритмический язык (как и любой другой язык), образуют три его составляющие: алфавит, синтаксис и семантика.
Алфавит – фиксированный для данного языка набор символов (букв, цифр, специальных знаков и т.д.), которые могут быть использованы при написании программы.
Синтаксис - правила построения из символов алфавита специальных конструкций, с помощью которых составляется алгоритм.
Семантика - система правил толкования конструкций языка. Таким образом, программа составляется с помощью соединения символов алфавита в соответствии с синтаксическими правилами и с учетом правил семантики.
Основные элементы алгоритмического языка
Основными понятиями в алгоритмических языках являются следующие.
Имена (идентификаторы) - последовательность символов для обозначения объектов программы (переменных, массивов, функций и дp.).
Операции. Существуют следующие типы операций:
- арифметические операции: сложение, обозначается символом “+”; вычитание, обозначается символом “-”; умножение, обозначается символом “*”; деление, обозначается символом “/”; возведение в степень обозначается символом “^”;
- логические операции: операции “логическое и”, “логическое или”, “логическое не” и др.;
- операции отношения: меньше, обозначается символом “<”; больше, обозначается символом “>”; меньше или равно, обозначается символами “<=”; больше или равно, обозначается символами “>=”; равно, обозначается символом “=”; не равно, обозначается символами “<>”.
- операция конкатенации символьных значений дpуг с другом, изображается знаком "+".
Ключевые слова – это слова языка, имеющие строго определенное назначение, которые не могут использоваться в качестве идентификаторов.
Данные - величины, обрабатываемые программой. Имеется тpи основных вида данных: константы, переменные и массивы.
Константы - это данные, которые зафиксированы в тексте программы и не изменяются в процессе ее выполнения.
Примеры констант:
числовые: 7.5, 12;
строковые: "abcde", "информатика".
Переменные – это данные, которые могут изменять свои значения в ходе выполнения программы. Они обозначаются именами. Переменные бывают целые, вещественные, и строковые.
Массивы - последовательности однотипных элементов, число которых фиксировано и которым присвоено одно имя. Положение элемента в массиве однозначно определяется его индексами - одним в случае одномерного массива, или несколькими, если массив многомерный.
Выражения – элементы языка, которые предназначаются для выполнения необходимых вычислений, состоят из констант, переменных, указателей функций, объединенных знаками операций. Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, "многоэтажных" дробей и т. д.), что позволяет вводить их в компьютер, последовательно нажимая на соответствующие клавиши клавиатуры.
Различают выражения арифметические, логические и строковые.
Арифметические выражения служат для определения одного числового значения. Арифметические выражения записываются по следующим правилам:
1. Нельзя опускать знак умножения между сомножителями и ставить рядом два знака операций.
2. Индексы элементов массивов записываются в скобках.
3. Операции выполняются в порядке старшинства: сначала вычисление функций, затем возведение в степень, потом умножение и деление и в последнюю очередь - сложение и вычитание.
4. Операции одного старшинства выполняются слева направо.
Логические выражения описывают некоторые условия, которые могут удовлетворяться или не удовлетворяться. Таким образом, логическое выражение может принимать только два значения - "истина" или "ложь" (да или нет).
В записи логических выражений помимо арифметических операций сложения, вычитания, умножения, деления и возведения в степень используются операции отношения и логические операции.
Значения строковых выражений - тексты. В них могут входить строковые константы, строковые переменные и строковые функции, разделенные знаком операции конкатенации.
Оператор – это элемент языка, который задает полное описание некоторого действия, которое необходимо выполнить. Оператор - это наиболее крупное и содержательное понятие языка: каждый оператор представляет собой законченную фразу языка программирования и определяет некоторый вполне законченный этап обработки данных. В состав операторов входят ключевые слова; данные; выражения и т.д.
Стандартная функция – подпрограмма, заранее встроенная в транслятор языка для вычисления часто употребляемых функций. В качестве аргументов функций можно использовать константы, переменные и выражения.
Программа - это последовательность инструкций, предназначенных для выполнения компьютером. В настоящее время программы оформляются в виде текста, который записывается в файлы.
Программирование – это теоретическая и практическая деятельность решения задачи средствами конкретного языка программирования и оформления полученных результатов в виде программы.
На стадии программирования возникает этап отладки программы – процесс обнаружения и устранения ошибок в программе, производимой по результатам ее тестирования на компьютере.
После окончательной отладки программа документируется, т.е. к ней прилагается описание назначения программы и инструкция по эксплуатации. Только после этого программа становится законченным программным продуктом, подготовленным к реализации как любой иной вид промышленной продукции.
Языки высокого уровня работают через трансляционные программы - трансляторы, которые преобразуют исходный код в последовательность команд машинного языка. Существует два основных вида трансляторов: интерпретаторы, которые сканируют и проверяют исходный код в один шаг, и компиляторы, которые сканируют исходный код для создания текста программы на машинном языке, которая затем выполняется отдельно.
В общем случае программа может иметь модульную структуру, т.е. состоять из нескольких программных единиц, связанных между собой командами передачи управления. Такой принцип построения программ называется модульным. Программная единица, с первой команды которой начинается выполнение программы, называется головной программой. Остальные программные единицы, входящие в единую программу, называются подпрограммами.
Подпрограмма - это последовательность операторов, которые определены и записаны только в одном месте программы, однако их можно вызвать для выполнения из одной или нескольких точек программы.
Функция - это программная единица, которая может быть употреблена в выражении. Функция прямо возвращает величину, которая используется при вычислении этого выражения, и, кроме того, может возвращать величины через параметры.
Процесс разработки многомодульных программ эффективнее, особенно если разрабатывается программа большого размера, когда над реализацией проекта может работать несколько программистов, каждый из которых имеет возможность модифицировать фрагменты программы, не мешая работе остальных.
Подпрограммы и функции позволяют создавать большие структурированные программы, которые можно делить на части. Это дает преимущества в следующих ситуациях:
1. Если программа большая, разделение ее на части облегчает создание, тестирование и ее сборку.
2. Если программа большая и повторная компиляция всего исходного текста занимает много времени, разделение ее на части экономит время компиляции.
3. Если процедуру надо использовать в разных случаях разным образом, можно записать ее в отдельный файл и скомпилировать отдельно.
Инструментальные системы программирования
Для популярных языков программирования на ЭВМ существует множество систем программирования. Программисты предпочитают те системы, которые легки в использовании, позволяют получить эффективные программы, имеют богатые библиотеки функций (подпрограмм) и мощные возможности для отладки разрабатываемых программ. В качестве примеров таких систем программирования можно назвать Delphi, Visual C++, Visual Basic.
Системы программирования прежде всего различаются по тому, какой язык программирования они реализуют. Среди программистов, пишущих программы для персональных компьютеров, наибольшей популярностью пользуются языки Си, Паскаль и Бейсик.
Для перевода текста программы на машинный язык применяются специальные программы ТРАНСЛЯТОРЫ, которые бывают двух типов: компиляторы (переводят текст программы на машинный язык один раз), интерпретаторы (переводят текст программы на машинный язык каждый раз при запуске программы на исполнение).
Приложение 2. Стандартные встроенные математические функции
| Обозначение в математике | Запись на BASIC | Пояснения |
| SIN X | SIN(X) | Аргумент в радианах |
| COS X | COS(X) | Аргумент в радианах |
| tg (X) | TAN(X) | Аргумент в радианах |
| ex | EXP(X) | Экспоненциальная функция, где е= 2,7182...., x <= 78 |
| ln X | LOG(X) | Функция натурального лога- рифма (по основанию е), X>0 |
| êX ê | ABS(X) | Модуль числа X |
| arctg X | ATN(X) | Результат в радианах |
| Выделение целой части числа X | INT(X) | Y=INT(4.2) | y=4 Y=INT(-4.2) | y=-5 |

| SQR(X) | X  0 0
|
Примеры записи встроенных функций:
| В математике | В BASIC |
| êln у ê | ABS(LOG(Y)) |
 ex+2 ex+2
| EXP(X+2) |
| Sin22x | Sin(2*x)^2 |
 
| ((a+b*x)/(a*x-b))^(1/3) |
ATN(X)
Приложение 3. Основные сведения об операторах VBA
Функция MsgBox
MsgBox(coo6щениe[, кнопки][, заголовок][, файл справки, контекст])
Выводит на экран диалоговое окно, содержащее сообщение, устанавливает режим ожидания нажатия кнопки пользователем, а затем возвращает значение типа Integer, указывающее, какая кнопка была нажата.
Оператор InputBox
Переменная=InputBox(сообщение[, заголовок][, умолчание][, Хпоз][, Y поз] [,файл справки, контекст])
Выводит на экран диалоговое окно, содержащее сообщение и поле ввода, устанавливает режим ожидания ввода текста пользователем или нажатие кнопки, а затем присваивает значение типа String, содержащее текст, выведенный в окне.
Условный оператор IF
Для проверки одного условия и выполнения оператора или блока операторов используется оператор IF...THEN. Этот оператор можно использовать с разным синтаксисом: однострочным (линейным) и многострочным (блочным).
а) Однострочный:
if<условие> Then <оператор>
б) блочный:
if<ycлoвue> Then
<блок операторов>
End if
Для проверки одного условия и выбора одного из двух блоков операторов используется оператор вида If...Then... Else
If <условие> Then
<блок операторов1>
Else
<блок операторов2>
End If
Для проверки более одного условия и выполнения одного из нескольких блоков операторов используется оператор вида:
If...Then...ElseIf
if<условие 1>Then
<блок операторов 1>
Elseif <условие 2> Then
<блок операторов 2>
…………………………..
Elseif<условие n > Then
<блок операторовп >
Else
<блок операторов Else>
End If
Оператор выбора SELECT CASE
Используется для проверки одного условия и выполнения одного из нескольких блоков операторов.
Формат записи оператора:
Select Case проверяемое выражение
Case список выражений 1
операторы I
Case список выражений 2
операторы 2
Case список выражений 3
операторы 3
…………………
Case Else
операторы группы Else
End Select
Проверяемое выражение вычисляется в начале работы оператора Select Case. Это выражение может возвращать значение любого типа (логическое, числовое, строковое).
Список выражений - одно или несколько выражений, разделенных стандартным символом – разделителем (;).
При выполнении оператора проверяется, соответствует ли хотя бы один из элементов этого списка проверяемому выражению. Эти элементы списка выражений могут иметь одну из следующих форм:
- выражение
- выражение 1 Tо выражение 2
- Is логический оператор (оператор сравнения) выражение
Например, Is>= 10
Оператор цикла For...Next имеет две разновидности:
а) For счетчик = начало То конец [Step приращение]
операторы
Next [счетчик]
б) For Each <элемент> In <группа>
операторы
Next [элемент]






