Рассмотрим пример нахождения корней уравнения
x3- 0,01x2-0,7044x + 0,139104 =0.
1. Отметим, что у полинома третьей степени имеется не более трех вещественных корней. Для нахождения корней их предварительно нужно локализовать. С этой целью необходимо построить график функции или ее протабулировать. Например, протабулируем наш полином на отрезке [-1, 1] с шагом 0,2. Результат табуляции приведен на рисунке, где в ячейку B2 введена следующая формула:

=A2 ^ 3 – 0.01*A2 6 2 – 0.7044*A2 + 0.139104
Из рисунка видно, что полином меняет знак на интервалах [-1, -0,8], [0,2, 0,4], [0,6, 0,8]. Это означает, что на каждом из них имеется корень данного полинома. Поскольку полином третьей степени имеет не более трех действительных корней, значит мы локализовали все его корни.
2. Далее нужно задать относительную погрешность вычислений и предельное число итераций. Выберем команду Сервис, Параметры. В диалоговом окне Параметры на вкладке Вычисления зададим относительную погрешность 0.00001 и предельное число итераций – 1000.
3. В качестве начальных значений приближений к корням можно взять любые точки из отрезков локализации корней. Возьмем, например, их средние точки: -0.9, 0.3 и 0.7 и введем их в диапазон ячеек С2:С4. В ячейку D2 введем формулу
= C2 ^ 3 – 0.01*C2 ^ 2 – 0.7044*C2 + 0/139104
Выделим эту ячейку и с помощью маркера заполнения протащим введенную в нее формулу на диапазон D2:D4. Таким образом, в ячейках D2:D4 вычисляются значения полинома при значениях аргумента, введенного в ячейки С2:С4, соответственно.
4. Теперь выберем команду Сервис, Подбор параметров и заполним диалоговое окно Подбора параметра следующим образом.
Для нахождения корня уравнения с помощью средства подбора параметров надо записать уравнение так, чтобы его правая часть не содержала переменную.
В поле Установить в ячейке введем D2. Отметим, что в этом поле дается ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения. Вводить ссылки на ячейки в поля диалогового окна Подбор параметра удобнее не с клавиатуры, а щелчком на соответствующей ячейке. При этом Excel автоматически будет превращать их в абсолютные ссылки.
В поле Значение вводим 0. В поле Изменяя значение ячейки введем C2 (аналогично D2).
После нажатия кнопки OK средство подбора параметров находит приближенное значение корня, которое помещает в ячейку С2. В данном случае оно равно –0.919999.
Аналогично находим два оставшихся корня в ячейках С3 и С4: 0.20999 и 0.71999.
Вариант 1

b) Построить в одной системе координат при х Î[-2,2] графики следующих двух функций:
с) Построить поверхность
 |
d) Найти все корни уравнения
 |
Вариант 2

b) Построить в одной системе координат при х Î[-2,2] графики следующих двух функций:

с) Построить поверхность
 |
d) Найти все корни уравнения
Вариант 3

b) Построить в одной системе координат при х Î[-2,2] графики следующих двух функций:
 |
с) Построить поверхность
 |
d) Найти все корни уравнения


Вариант 4

b) Построить в одной системе координат при хÎ[-2,2] графики следующих двух функций: 
с) Построить поверхность
 |
при х,yÎ[-1,1]
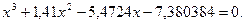 |
d) Найти все корни уравнения

Вариант 5
 |  | ||
b) Построить в одной системе координат при х Î[0,3] графики следующих двух функций:

с) Построить поверхность
 |
 |
d) Найти все корни уравнения

Вариант 6

b) Построить в одной системе координат при х Î[-3,0] графики следующих двух функций: 
 |
с) Построить поверхность
 |
 |
d) Найти все корни уравнения

Вариант 7

b) Построить в одной системе координат при х Î[-3,0] графики следующих двух функций: 
 |
с) Построить поверхность
 |
 |
d) Найти все корни уравнения

Вариант 8

b) Построить в одной системе координат при х Î[-3,0] графики следующих двух функций: 
 |

с) Построить поверхность при х Î[-1,1]
 |
d) Найти все корни уравнения
 |

Вариант 9

b) Построить в одной системе координат при хÎ[0,2] графики следующих двух функций:
с) Построить поверхность
 |
при х,y Î[-1,1]
d) Найти все корни уравнения


Вариант 10

b) Построить в одной системе координат при хÎ[0,2] графики следующих двух функций: 
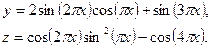 |
с) Построить поверхность
 |
d) Найти все корни уравнения





