МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ИнЭИ (в.о)
Семестр, 22, 2016/2017 уч. год
ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА
1. Предел функции в точке. Единственность предела, ограниченность функции, имеющей предел.
2. Бесконечно малые функции. Теорема о связи функции, ее предела и бесконечно малой. Свойства бесконечно малых функций. Предел суммы, произведения и частного. Переход к пределу в неравенствах.
3. Непрерывность функции в точке. Непрерывность основных элементарных функций. Теоремы о переходе к пределу под знаком непрерывной функции, о непрерывности сложной функции.
4. Замечательные пределы. Эквивалентные бесконечно малые, их таблица. Теорема о замене бесконечно малых эквивалентными при вычислении пределов.
5. Сравнение бесконечно малых функций. Бесконечно большие функции. Связь бесконечно больших и бесконечно малых функций.
6. Односторонние пределы. Точки разрыва функций, их классификация. Предел функции в бесконечности.
7. Производная, ее геометрический и механический смысл. Уравнение касательной и нормали к графику функции. Таблица производных.
8. Дифференцируемость функции, дифференциал. Необходимое и достаточное условие дифференцируемости. Геометрический смысл дифференциала.
9. Непрерывность дифференцируемой функции. Производная суммы, произведения и частного. Производная сложной функции. Приближенные вычисления с помощью дифференциала.
10. Производная обратной функции. Производные обратных тригонометрических функций.
11. Производные и дифференциалы высших порядков.
12. Производная функции, заданной параметрически.
13. Свойства функций, непрерывных на отрезке.
14. Теоремы Ролля, Лагранжа, Коши.
15. Правило Лопиталя.
16. Формула Тейлора с остаточными членами в форме Лагранжа и Пеано. Представление функций 
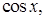
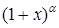по формуле Тейлора.
17. Условия возрастания и убывания функций на интервале.
18. Экстремумы функции. Необходимое и достаточное условия существования экстремума. Наибольшее и наименьшее значения функции на отрезке.
19. Направление выпуклости графика функции. Достаточное условие выпуклости. Точки перегиба. Необходимое и достаточное условия точки перегиба.
20. Исследование на экстремум с помощью производных высших порядков. Общая схема исследования функции и построения графика.
21. Первообразная функции. Теорема об общем виде первообразной. Неопределенный интеграл, его свойства. Таблица неопределенных интегралов.
22. Замена переменной и интегрирование по частям в неопределенном интеграле.
23. Определенный интеграл, его геометрический и физический смысл. Свойства определенного интеграла.
24. Производная определенного интеграла с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница.
25. Интегрирование по частям и замена переменной в определенном интеграле.
26. Интегрирование рациональных выражений.
27. Интегрирование тригонометрических и иррациональных выражений.
28. Вычисление площади плоской фигуры в декартовых и полярных координатах.
29. Вычисление длины дуги плоской кривой, заданной в декартовых и полярных координатах или параметрически.
30. Несобственные интегралы с бесконечными пределами интегрирования.
ПРИМЕРЫ ДЛЯ ЭКЗАМЕНАЦИОННЫХ БИЛЕТОВ
I. Вычислить предел функции.
1. 
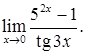
| 2. 
| 3. 
| 4. 
|
5. 
| 6. 
| 7.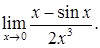 
| 8. 
|
II. Найти производную.
9. 
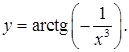
| 10. 
| 11. 
|
III. Найти производную 
.
12. 
|
IV. Найти вторую производную.
13. 
|
V. Написать уравнение касательной и нормали к графику функции в заданной точке.
14. 
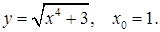
| 15. 
|
VI. Написать формулу Тейлора n -го порядка в точке x 0.
16. 
|
VII. Найти интервалы монотонности и экстремумы функции.
17. 
| 18. 
| 19. 
|
VIII. Найти наибольшее и наименьшее значение функции на отрезке.
20. 
|
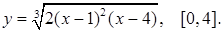
IX. Провести полное исследование функции и построить график.
21. 
| 22. 
| 23. 
| |
24. 
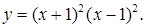
| 25. 
|
X. Найти интеграл.
26. 
| 27. 
| 28. 
| 29. 
|
30. 
| 31. 
| 32. 
| 33. 
|
34. 
|
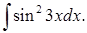
XI. Вычислить интеграл.
35. 
| 36. 
| ||
37. 
| 38. 
|
XII. Вычислить площадь фигуры, ограниченной кривыми.
39. 
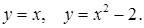
| 40. 
| ||
41. 
|
XIII. Вычислить площадь фигуры, ограниченной кривыми, заданными параметрически.
42. 
| 43.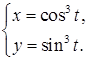 
|
XIV. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах.
44. 
| 45. 
|
XV. Вычислить длину дуги кривой.
46. 
| 47. 
|
XVI. Исследовать на сходимость несобственный интеграл.
48. 
| 49. 
| 50. 
|
