Решение задачи требует знаний закона Ома для всей цепи и ее участков, законов Кирхгофа, методики определения эквивалентного сопротивления цепи при смешанном соединении резисторов, а также умения вычислять мощность и работу электрического тока. Содержания задач и схемы цепей приведены в условии, а данные к ним — в табл. 1. Перед решением задачи рассмотрите типовой пример 1.
Пример 1. Для схемы, приведенной на рис. 1 а, определить эквивалентное сопротивление цепи RAB и токи в каждом резисторе, а также расход электроэнергии цепью за 8 ч работы.
Решение. Задача относится к теме “Электрические цепи постоянного тока”. Проводим поэтапное решение, предварительно обозначив стрелкой ток в каждом резисторе; индекс тока должен соответствовать номеру резистора, по которому он проходит.
1. Определяем общее сопротивление разветвления RCD, учитывая, что резисторы R3 и R4 соединены последовательно между собой, а с резистором R5 — параллельно: RCD = (R3 + R4)R5/(R3 + R4 + R5) = (10 + 5) •10/(10 + 5 + 10) = 6 Ом (рис. 1,б).
2. Определяем общее сопротивление цепи относительно вводов CE. Резисторы RCD и R2 включены параллельно, поэтому RCE = RCDR2/(RCD + R2) = 6•3/(6 + 3) = 2 Ом (рис. 1, в).
3. Находим эквивалентное сопротивление всей цепи: RAB = R1 + RCE = 8 + 2 = 10 Ом (рис. 1, г).
4. Определяем токи в резисторах цепи. Так как напряжение UAB приложено ко всей цепи, а RAB = 10 Ом, то согласно закону Ома I1= UAB/RAB= 150/10= 15 А.
Внимание! Нельзя последнюю формулу писать в виде I1= UAB/R1, так как UAB приложено ко всей цепи, а не к участку R1.
Для определения тока I2 находим напряжение на резисторе R2, т. е.UCE. Очевидно, UCE меньше UAB на потерю напряжения в резисторе R1, т. е. UCE = UAB — I1R1= 150 — 15•8 = 30 В. Тогда I2 == UCE/R2= 30/3= 10 А. Так как UCE = UCD, то можно определить токи I3,4 и I5. I3,4 = UCD/(R3+R4) = 30/(10 + 5) = 2 А; I5 = UCD/R5 = 30/10= 3 А.
На основании первого закона Кирхгофа, записанного для узла С, проверим правильность определения токов:
I1 = I2 + I3,4 + I5, или 15 = 10 + 2 + 3 = 15 А.
5. Расход энергии цепью за восемь часов работы:
W = Pt = UABI1t = 150•15•8 = 18000 Bт•ч = 18 кВт•ч
Пусть в схеме примера 1 известны сопротивления всех резисторов, а вместо напряжения UAB задан один из токов, например I2=2 А. Найти остальные токи и напряжение UAB. Зная I2, определяем UCE = I2R2 =2 ×3=6 В. Так как UCE = UCD, то
I3,4 = UCD/(R3+R4)=6/(10 + 5) = 0,4 А;
I5 = UCD/R5 = 6/10 =0,6 А.
На основании первого закона Кирхгофа I1 = I2+I3,4+I5 = 2 + 0,4 + 0,6 = 3 А. Тогда UAB = UCE + I1R1 = 6 + 3×8 = 30 В.
При расплавлении предохранителя Пр5 и резистор R5 выключается и схема принимает вид, показанный на рис. 1, д. Вычисляем эквивалентное сопротивление схемы: 
=R1+(R3+R4)R2/(R3+R4+R2) = 8+(10 + 5)•3/(10 + 5 + 3) = 10,5 Ом. Так как напряжение UAB остается неизменным, находим ток I1 = UAB / = 150/10,5 = 14,28 А. Напряжение UCE = UAB — I1R1 = 150 — 14,28×8 = 35,75 В.
Тогда токи
I2 = UCE/R2 = 35,75/3 = 11,9A; I3,4 = UCE/R3,4 = 35,75/(10+5) = 2,38A
 |
Сумма этих токов равна току I1: 11,9 + 2,38 = 14,28 А.
рисунок 1
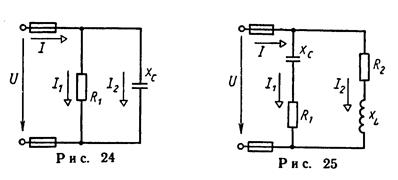
Задача 2 (варианты 01—25). Неразветвленная цепь переменного тока, показанная на соответствующем рисунке, содержит активные и реактивные сопротивления, величины которых заданы в табл. 2. Кроме того, известна одна из дополнительных величин (U, I, P, Q, S). 5). Определить следующие величины, если они не заданы в таблице 2 вариантов: 1) полное сопротивление цепи Z; 2) напряжениеU, приложенное к цепи; 3) силу тока в цепи; 4) угол сдвига фаз ф (величину и знак); 5) активную Р, реактивную Q и полную S мощности, потребляемые цепью. Начертить в масштабе векторную диаграмму цепи и пояснить ее построение. С помощью логических рассуждений пояснить, как изменится ток в цепи и угол сдвига фаз, если частоту тока увеличить вдвое. Напряжение, приложенное к цепи, считать неизменным.
Указание. См. решение примера 2.
Таблица 2
| Номер вариантов | Номер рисунков | R1, Ом | R2, Ом | XL1, Ом | XL2, Ом | XC1, Ом | XC2, Ом | Дополнительная величина |
| — | — | I = 10 A | ||||||
| — | — | P = 120 Bт | ||||||
| — | — | P2 = 100 Bт | ||||||
| — | — | U1 = 72 B | ||||||
| — | — | U = 40 B | ||||||
| — | — | Q1 = - 96 вар | ||||||
| — | — | Q = - 640 вар | ||||||
| — | — | QС1 = -125 вар | ||||||
| — | — | S = 80 B•A | ||||||
| — | — | P1 = 32 Bт | ||||||
| — | — | U = 40 B | ||||||
| — | — | P = 16 Bт | ||||||
| — | — | QL1 = 135 вар | ||||||
| — | — | QL2 = 16 вар | ||||||
| — | — | QC1 = - 20 вар | ||||||
| — | — | P1 = 48 Вт | ||||||
| — | — | U2 = 12 В | ||||||
| — | — | QC1 = —720 вар | ||||||
| — | — | I = 5 А | ||||||
| — | — | S = 500 В•А | ||||||
| — | — | P = 100 Вт | ||||||
| — | — | UC2 = 40 В | ||||||
| — | — | I = 1 А | ||||||
| — | — | QC2 = —240 вар | ||||||
| — | — | P1 = 432 Вт |
 |
 |
 |
Задача 3 (варианты 01—00). Разветвленная цепь переменного тока состоит из двух параллельных ветвей, содержащих в зависимости от варианта активные сопротивления R1, R2. и реактивные XL и XC. Полные сопротивления ветвей Z1 и Z2. К цепи приложено напряжение U.Токи в ветвях соответственно равны I1 и I2; ток в неразветвленной части цепи равен I. Ветви потребляют активные мощности P1 и Р2 и реактивные Q1 и Q2. Общие активная и реактивная мощности цепи P и Q, а полная мощность цепи S. В табл. 3 указан также номер рисунка со схемой цепи. Определить значения, отмеченные прочерками в таблице вариантов, и начертить в масштабе векторную диаграмму цепи. Перед построением диаграммы вычислите углы сдвига фаз 
, 
; и 
. Какие изменения произойдут в цепи при ее включении на постоянное напряжение?
Указание. См. решение примера 3.
Таблица № 3
| № вар-та | № рис - ка | R1, Ом | R2, Ом | ХL Ом | ХC, Ом | Z1, Ом | Z2, Ом | U, В | I1, А | I2, А | I, А | P1, Вт | Q1, вар | P2, Вт | Q2, вар | P, Вт | Q, вар | S, B•A |
| » | — | — | — | — | — | » | — | — | — | — | — | — | ||||||
| » | — | — | — | — | — | — | » | — | — | — | — | — | ||||||
| » | — | — | — | — | — | — | » | — | — | — | — | — | ||||||
| » | — | — | — | — | — | — | — | » | — | — | — | — | ||||||
| » | — | — | — | — | — | — | — | — | » | — | — | — | ||||||
| » | — | — | — | — | — | — | » | — | — | — | — | — | ||||||
| » | — | — | — | — | — | — | — | — | 1,6 | » | — | — | — | — | ||||
| » | — | — | — | — | — | » | — | — | — | — | — | — | ||||||
| » | — | — | — | — | — | — | » | — | — | — | — | — | ||||||
| » | — | — | — | — | — | — | — | » | — | — | — | — | ||||||
| » | — | — | — | — | — | » | — | — | » | — | — | — | ||||||
| — | — | » | — | — | — | » | — | — | » | — | — | — | ||||||
| — | — | » | — | — | — | — | — | — | » | — | — | — | ||||||
| — | » | — | — | — | — | — | 8,95 | — | — | — | » | — | ||||||
| — | — | » | — | — | — | — | — | — | — | — | — | — | ||||||
| — | » | — | — | — | — | — | — | — | — | — | — | — | ||||||
| — | » | — | — | — | — | — | — | — | — | » | — | — | — | |||||
| » | — | — | — | — | — | — | — | — | » | — | — | — | ||||||
| — | — | » | — | — | — | — | — | — | » | — | — | — | ||||||
| — | » | — | — | — | — | — | — | — | — | » | — | — | ||||||
| » | » | — | — | — | — | — | — | » | » | — | — | — | — | |||||
| — | » | » | — | — | — | — | — | » | — | — | — | — | — | |||||
| » | » | — | — | — | — | — | — | — | » | — | — | — | — | |||||
| — | » | » | — | — | — | — | — | » | — | — | — | — | — | |||||
| — | » | » | — | — | — | — | — | — | » | — | — | — | — |
 | |||
 |
 |
Методические указания к решению задач 2—3
Эти задачи относятся к неразветвленным и разветвленным цепям переменного тока. Перед их решением изучите материал темы «Однофазные электрические цепи переменного тока», ознакомьтесь с методикой построения векторных диаграмм и разберите решение от примеров 2,3 в данных методических указаниях.
Пример 2. Неразветвленная цепь переменного тока содержит катушку с активным, сопротивлением R1 = 3 Ом и индуктивным XL = 12 Ом, активное сопротивление R2 = 5 Ом и конденсатор с сопротивлением Хс = 6 Ом (рис. 2,а). К цепи приложено напряжение U = 100В (действующее значение). Определить: 1) полное сопротивление цепи; 2) ток; 3) коэффициент мощности; 4) активную, реактивную и полную мощности; 5) напряжение на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи.
Решение. 1. Определяем полное сопротивление цепи:
2. Определяем ток цепи
I = U /Z = 100/10= 10 А.
3. Находим коэффициент мощности цепи. Во избежание потери знака угла (косинус — функция четная) определяем sin : sin = (XL — ХC)/Z = (12 — 6)/10 = 0,6; = 36°50'. По таблицам Брадиса определяем коэффициент мощности соs = соs 36°50' = 0,8.
4. Определяем активную, реактивную и полную мощности цепи:
P = UI 
= 100•10•0,8=800 Вт или P = I2(R1 + R2) = 102(3+5) = 800 Вт;
Q = I2(ХL — ХC) = 102(12 — 6) = 600 вар или Q = UI 
= 1000•10•0,6 = 600 вар;
S = UI= 100•10= 1000 В•А или S = I2Z = 102•10= 1000 В•А
или 
= 1000 В•А.
5. Определяем падения напряжения на сопротивлениях цепи:UR1 = I•R1 =10•3=30 В; UL = I•ХL = 10•12 = 120 В; UR2 = I•R2 = 10•5 = 50 В; UC = I•ХC = 10•6 = 60 В.
Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см — 2,0 А и масштабом по напряжению: в 1 см — 20 В. Построение векторной диаграммы (рис. 2, б) начинаем с вектора тока, который откладываем по горизонтали в масштабе 10 А/2 А/см = 5 см.
Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях UR1 иUR2 - 30 В/20 В/см = 1,5 см; 50 В/20 В/см = 2,5 см.
Из конца вектора UR2 откладываем в сторону опережения вектора тока на 90° вектор падения напряжения UL на индуктивном сопротивлении длиной 120 В/20 В/см = 6 см. Из конца вектора UL откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе UC длиной 60 В/20 В/см = 3 см. Геометрическая сумма векторовUR1, UR2, UL, UC равна полному напряжению, приложенному к цепи.
 |
Рисунок 2
Пример 3. Цепь переменного тока состоит из двух ветвей, соединенных параллельно. Первая ветвь содержит катушку с активным R1 = 12 Ом и индуктивным XL = 16 Ом сопротивлениями; во вторую ветвь включен конденсатор с емкостным сопротивлением XC = 8 Ом. и последовательно с ним активное сопротивление R2 = 6 Ом. Активная мощность, потребляемая первой ветвью P1 = 48 Вт (рис. 3, а). Определить: 1) токи в ветвях и в неразветвленной части цепи; 2) активные и реактивные мощности цепи; 3) напряжение, приложенное к цепи; 4) угол сдвига фаз между током в неразветвленной части цепи и напряжением. Начертить в масштабе векторную диаграмму цепи.
Решение. 1. Активная мощность P1 теряется в активном сопротивлении R1. Поэтому 
. Отсюда
= 2 А.
2. Определяем напряжение, приложенное к цепи:
= 40 В.
3. Определяем ток:
= 4 A.
4. Находим активную и реактивную мощности, потребляемые цепью:
= 22•12 + 42•6 = 154 Вт;
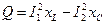= 22•16 — 42•8 = —64 вар.
Знак “—” показывает, что преобладает реактивная мощность емкостного характера.
Полная мощность, потребляемая цепью:
= 166,8 В•А.
5. Определяем ток в неразветвленной части цепи:
= 4,17 A
6. Угол сдвига фаз во всей цепи находим через 
во избежание потери знака угла:
= —64/166,8 = —0,384; = —22°35'.
Знак “—” подчеркивает, что ток цепи опережает напряжение UAB
Для построения векторной диаграммы определяем углы сдвига фаз в ветвях:
; 
; 
 |
Задаемся масштабом по току: в 1 см — 1 А и напряжению: в 1 см — 5 В. Построение начинаем с вектора напряжения (рис. 3,6). Под углом
к нему в сторону отставания откладываем в масштабе вектор тока I1; под углом 
в сторону опережения —вектор тока I2. Геометрическая сумма этих токов равна току в неразветвленной части цепи.
Рисунок 3
Задача 4 (варианты 01—25). Три группы сопротивлений соединили звездой с нулевым проводом и включили в трехфазную сеть переменного тока с линейным напряжением UНОМ. Активные сопротивления в фазах А, В и С соответственно равны RA, RB и RC, реактивные — ХA, ХB и ХC. Характер реактивных сопротивлений (индуктивное или емкостное) указан на схеме цепи. Углы сдвига фаз в каждой фазе равны 
, 
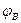и . Линейные токи (они же фазные) в нормальном режиме равны IA, IB и IC. Фазы нагрузки потребляют активные мощности PA, PB и PC и реактивные QA, QB и QC. В таблице вариантов указаны некоторые из этих величин и номер рисунка цепи. Для своего варианта начертить схему цепи; определить величины, отмеченные прочерками в табл. 4, и начертить в масштабе векторную диаграмму цепи в нормальном режиме. Начертить векторную диаграмму цепи в аварийном режиме при отключении фазы А. Из векторных диаграмм определить графически токи в нулевом проводе в обоих режимах. При вычислениях принять: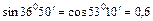 
Указание. См. решение примера 4.
 |
 |
