A. Целые числа без знака
Целые числа без знака обычно занимают в памяти компьютера:
- один байт, в этом формате можно представить двоичные числа в диапазоне от 00000000 до 111111111 или в десятичном представлении от 0 до 255 (0 … 28 – 1);
- два байта, соответственно диапазон представляемых чисел в десятичной системе счисления будет от 0 до 65535 (0 … 216 – 1).
Пример 1. Представить число 7210 = 10010002 в однобайтовом формате:
| Номера разрядов | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Биты числа |
B. Целые числа со знаком
Целые числа со знаком обычно занимают в памяти компьютера:
- один байт, в этом формате можно представить двоичные числа в диапазоне от –0000000 до +11111111 или в десятичном представлении от -128 до 127 (–27 … 27 – 1);
- два байта, соответственно диапазон представляемых чисел в десятичной системе счисления –32768 до 32767 (–215 … 215 – 1);
- четыре байта, диапазон представляемых чисел в десятичной системе счисления от
–2147483648 до 2147483647 (–231... 231–1).
При этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» – единицей. Число располагаем в разрядной сетке так, чтобы цифра младшего разряда числа занимала крайнюю правую ячейку.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.
Для представления отрицательных чисел применяется обратный, или дополнительный коды. Они применяются для выполнения операции вычитания, которую заменяют операцией сложения чисел с разными знаками: a – b = a + (–b).
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде.
Прямой код целого числа
Под прямым кодом двоичного числа понимают запись самого числа. Знаковый разряд для положительных чисел определяют нулем (0), для отрицательных – единицей (1).
Пример 2. Представить положительное число 6910= 10001012 в однобайтовом формате:
| Номера разрядов | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Биты числа |
Пример 3. Представить отрицательное число – 5910 = – 1110112 в однобайтовом формате:
| Номера разрядов | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| Биты числа |
П рямой код применяется только для представления положительных двоичных чисел. Отрицательные числа в прямом, обратном или дополнительном кодах имеют разное изображение.
Обратный код целого числа
Обратный код целого положительного числа совпадает с его прямым кодом.
Обратный код целого отрицательного числа получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы – нулями.
Дополнительный код целого числа
Дополнительныйкод целого положительного числа совпадает с его прямым кодом.
Дополнительный код для отрицательного числа образуется путем получения обратного кода с последующим прибавлением к младшему разряду единицы.
Обычно отрицательные десятичные числа при вводе в компьютер автоматически преобразуются в обратный или дополнительный коды и в таком виде хранятся и участвуют в операциях. При выводе таких чисел происходит обратное преобразование в отрицательные десятичные числа.
Пример 4. Переведите + 2710 и – 2710 в прямой, обратный и дополнительный коды.
| Число | Прямой код | Модуль числа | Обратный код | Дополнительный код | |
| + 2710 | +110112 | 0 0011011 | 0 0011011 | 0 0011011 | 0 0011011 |
| – 2710 | –110112 | 1 0011011 | 0 0011011 | 11100100 | 11100101 |
Практическое задание
1. Запишите следующие числа в прямом, обратном и дополнительном кодах.
А) 11010112; Б) –1010112; В) –1011012; Г) –11001112;
2. Арифметические действия над целыми числами
В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет упростить конструкцию компьютера.
При сложении чисел в знаковом разряде могут появиться две цифры, вторую единицу от запятой называют единицей переноса
При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.
При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.
Пример 5. Выполните сложение Х + Y = 15 – 5 =? в обратном и дополнительном кодах.
| Сложить числа | По правилам двоичной арифметики | В обратном коде | В дополнительном коде |
| Х = 1510 Y = – 510 Х + Y = 1010 | Х = 1111 Y = – 101 Х + Y = 1010 | Х обр = 0 0001111 Y обр = 1 1111010 1 0 0001001 Ä + 1 (Х + Y)обр = 0 0001010 | Х доп = 0 0001111 Y доп = + 1 1111011 1 0 0001001 отбрасывается Ã (Х + Y) доп = 0 0001010 |
Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах, кроме знакового, на противоположные. Дополнительный код преобразуется в прямой так же, как и обратный, с последующим прибавлением единицы к младшему разряду.
Пример 6. Выполните сложение Х + Y = – 5 – 7 =? в обратном и дополнительном кодах.
| Сложить числа | По правилам двоичной арифметики | В обратном коде | В дополнительном коде |
| Х = – 5 Y = – 7 Х + Y = –12 | Х = – 101 Y = – 111 Х + Y = –1100 | Х обр = 1 1111010 Y обр = + 1 1111000 1 1 1110010 Ä ð + 1 (Х + Y)обр= 1 1110011 | Х доп = 1 1111011 Y доп = + 1 1111001 1 1 1110100 Ã отбрасывается (Х + Y) доп= 1 1110100 |
Так как сумма является кодом отрицательного числа (знак 1), то необходимо перевести результаты в прямой код:
- из обратного кода: (Х + Y)обр = 1 1110011 ð (Х + Y)пр = 1 0001100
- из дополнительного кода: (Х + Y) доп = 1 1110100 ð (Х + Y)пр = 1 0001011 + 0 00000001,
(Х + Y)пр = 1 0001100.
3. Модифицированный обратный и дополнительный коды
При сложении может возникнуть ситуация, когда старшие разряды результата не помещаются в отведенной области памяти. Такая ситуация называется переполнением разрядной сетки формата числа.
Переполнение разрядной сетки может привести к переносу единицы в знаковый результат, что приведет к неправильному результату. Положительное число, получившееся в результате арифметической операции, может восприниматься как отрицательное, так как в знаковом разряде появится «1», и наоборот.
Например, Х = 0 1011110
Y = 0 1101100
Х + Y = 1 1001010
Х и Y – коды положительных чисел, но в процессе сложения в знаковом разряде появилась «1», что означает код отрицательного числа. Чтобы распознать переполнение разрядной сетки, вводятся модифицированные коды.
В модифицированных обратном и дополнительном кодах под знак числа отводится не один, а два разряда: «00» соответствует знаку «+», «11» – знаку «–». Любая другая комбинация («01» или «10»), получившаяся в знаковых разрядах, является признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем не отличается от сложения в обычных обратном и дополнительном кодах.
Пример 7. Даны два числа: Х = 101011 и Y = – 11110. сложить их в дополнительном и модифицированном дополнительных кодах.
| Обычная запись | Х = +0101011 | Y = – 0011110 |
| Обратный код | Х обр = 01010100 | Y обр = 1 1100001 |
| Модифицированный обратный код | 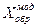 = 00 1010100 = 00 1010100
|  = 11 1100001 = 11 1100001
|
| Дополнительный код | Х доп = 01010101 | Y доп = 1 1100010 |
| Модифицированный дополнительный код |  = 00 1010101 = 00 1010101
|  = 11 1100010 = 11 1100010
|
| Дополнительный код | Модифицированный дополнительный код |
| Х доп = 0 0101011 Y доп = + 1 1100010 1 0 0001101 отбрасывается Ã (Х + Y) доп = 0 0001101 |  = 00 0101011 = 00 0101011
 = + 11 1100010
1 00 0001101
отбрасывается Ã = + 11 1100010
1 00 0001101
отбрасывается Ã
 = 00 0001101 = 00 0001101
|
4. Индивидуальные задания
по теме «Компьютерная арифметика»
1. Запишите числа Х и Y в прямом, обратном и дополнительном кодах. Выполните сложение в обратном и дополнительном кодах. Результат переведите в прямой код.
2. Измените число Х и Y, добавив в конце числа две единицы. Сложите полученные числа в модифицированном обратном и модифицированном дополнительных кодах. Результат переведите в прямой код. Выполните проверку сложения, используя правила двоичной арифметики.
| Вариант | Числа Х и Y | Вариант | Числа Х и Y |
| Х = –100101 Y = 11101 | Х = –101101 Y = 1101 | ||
| Х = –110101 Y = 11101 | Х = –1101111 Y = 10101 | ||
| Х = –1000111 Y = 11101 | Х = –1110001 Y = 10011 | ||
| Х = –1010001 Y = 10011 | Х = –1000011 Y = 10011 | ||
| Х = –1101001 Y = 10111 | Х = –1010001 Y = 1111 | ||
| Х = –101001 Y = 10111 | Х = –1010111 Y = 11100 | ||
| Х = –110101 Y = 1111 | Х = –101111 Y = 1101 | ||
| Х = –110101 Y = 10011 | Х = –1001011 Y = 10101 | ||
| Х = –100011 Y = 10011 | Х = –1010001 Y = 1011 | ||
| Х = –110001 Y = 10111 | Х = –1000111 Y = 11111 | ||
| Х = –111001 Y = 1110 | Х = –100001 Y = 1111 | ||
| Х = –1011101 Y = 10111 | Х = –1111000 Y = 101111 | ||
| Х = –1100000 Y = 1111 | Х = –10101 Y = 1101 |






