Введение
Учебная практика закрепляет все теоретические и практические знания, полученные в процессе обучения. Также является важной составляющей учебного процесса в формировании компетенции современного специалиста.
Цели учебной практики:
- работа с погрешностями и построение модели межотраслевого баланса;
- получение навыков установки виртуальной машины, операционной системы, прикладных программ, создание сайтов;
- знакомства с другими пакетами прикладных программ для решения задач технических вычислений.
Работа с погрешностями.
Говорят, что число a имеет m верных значащих знаков, если абсолютная погрешность ∆a этого числа не превышает половины единицы разряда, выражаемого m-й значащей цифрой.
Задание 1. а) Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и оцените погрешность искомого значения. б) Определите число верных знаков в результате. (Прямая задача)
Задание 2. Выясните погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами. (Обратная задача)
Решение задания 1.
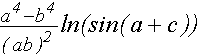
a=0.12456±0.0005
b=0.12078±0.00003
c=2.08±0.015
а) Пусть 
– точное значение, 
– приближенное значение.
Тогда абсолютной погрешностью числа называется величина 
, а относительной погрешностью –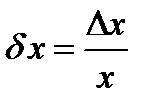 
.
Для арифметических операций справедливы следующие правила определения погрешностей.
d (xy)~d (x/y)<d x+d y, D (x±y)<D x+D y, d (x±y)<MAX(d x, d y) и D f(x)~f'(x) × D x:
Абсолютные погрешности исходных данных:
D a = 0,0005, D b = 0,00003, D c = 0,015.
Относительные погрешности исходных данных:
δa=0.004014129736673, δb=0.000248385434287, δc=0.007211538461538
Тогда:
| a^4=0.00024 => | δa^4=4*δa =0.0160565 => | Δa^4=0.00024*0.0160565=0.00000385356 |
| b^4=0.00021 => | δb^4=0.0009935 => | Δb^4=0.000000208635 |
| a^4-b^4=0.00003 | Δ(a^4-b^4)= =0.000003644925 | δ(a^4-b^4)=0.1214975 |
| a*b=0.0150443568 | Δ(a*b)=0.000000015 | δ(a*b)=0.0000009970516 |
| (a*b)^2=0.00022633267 | Δ((a*b)^2)= =0,00000000045 | δ((a*b)^2)=0.00000199 |
| (a^4-b^4)/(a*b)^2= =0.13254825298 | Δ ((a^4-b^4)/(a*b)^2)= =0,016104 | δ ((a^4-b^4)/(a*b)^2)= =0,121499 |
| a+c=2.20456 | Δ(a+c)=0.0155 | δ (a+c)=0.00703088144573 |
| sin(a+c)=0.8058 | Δ(sin(a+c))=|(sin(a+c))¢| × D (a+c)= =|cos(a+c)|D (a+c)= =0.5922*0.0155=0.00918 | δ (sin(a+c))=0,0113924 |
| ln(sin(a+c))=-0.2159197 | Δ(ln(sin(a+c)))=|(ln(sin(a+c)))¢|= =|1/sin(a+c)*(sin(a+c))¢|=0.0113924 | δ (ln(sin(a+c)))=- 0.0527622 |
| F = (a^4-b^4)/(a*b)^2 *ln(sin(a+c)) = =-0.02861978 | δF=δ ((a^4-b^4)/(a*b)^2) + δ(ln(sin(a+c)))= 0.0687368 | ΔF= F*ᵟF=0.0019672 |
б) Так как D F = 0.0019672, а F= -0.02861978, то m =4.
Таким образом, ответ: F = -0,028 61978
Решение задания 2.
F= 
a = 0.02456, b=0.01823, c=0.348, m=5
Находим:
a+b=0.04279,
a-b=0.00633,
(a-b)1/2=0.07956,
(a+b)/(a-b)1/2=0.53783,
a+c=0.37256,
sin(a+c)=0.364,
ln(sin(a+c))=-1.010599,
F=(a+b)/(a-b)1/2* ln(sin(a+c))=- 0.5435 3028 (полагаем первые 5 цифрверными).
Тогда ΔF<=0.0002
1. 
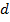F/ 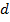a = ((a-b)1/2-(a+b) / (2*(a-b)1/2)) / (a-b) * ln(sin(a+c)) + (a+b)/(a-b)1/2 * cos(a+c)/sin(a+c) = =31.607148
= 0.0002/(3*31.607148) = 0.000002109
2. 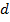F/ 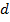b = ((a-b)1/2-(a+b) / (2*(a-b)1/2)) / (a-b) = 12.299805
= 0.0002/(3*12.299805) = 0.00000542
3. 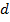F/ 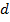c = cos(a+c)/sin(a+c) = 2.55878
Δc = 0.000026054
Модель межотраслевого баланса.
Целью построения модели МОБ является анализ потоков товаров между отраслями экономики, обеспечивающего соответствие объема выпуска суммарному спросу на товары.
При этом не различаем товары и ресурсы (затраты)
Как всякая модель МОБ является упрощением реальной ситуации.
Перечислим основные из них:
- пусть производственный сектор экономики разбит на n «чистых» отраслей.
- каждая отдельная отрасль производит только один продукт, и разные отрасли производят различные продукты.
Очевидно, что одни отрасли при своем производстве нуждаются в продукции других отраслей, т.е. выпуск каждого продукта либо затрачивается в производстве товаров либо удовлетворяет конечный спрос
ФОРМАЛИЗАЦИЯ:
Пусть xi – валовый продукт i-ой отрасли,
yi – конечный продукт i-ой отрасли.
Часть валового продукта потребляется другими отраслями, обозначим:
xi1 ,xi2 ,…, xin.
Всего на производственное потребление затрачивается:
Таким образом, возникает понятие баланса:
Изучая статистические данные экономисты, включая В. Леонтьева, заметили, что независимо от масштаба производства, коэффициенты, определяющие затраты i -й отрасли на производство единицы продукции j-й отрасли почти не меняются в годовом периоде производства
Определение: Коэффициенты, определяемые формулами (1) называют технологическими или коэффициентами прямых затрат.
Следовательно, баланс можно записать:
