КОМПЛЕКСН
Преобразует коэффициенты при вещественной и мнимой частях комплексного числа в комплексное число в форме x + yi или x + yj.
Синтаксис
КОМПЛЕКСН (действительная_часть; мнимая_часть;мнимая_единица)
Действительная_часть - это действительная часть комплексного числа.
Мнимая_часть - это мнимая часть комплексного числа.
Мнимая_единица - это обозначение мнимой единицы в комплексом числе. Если аргумент мнимая_единица опущен, то предполагается, что он равен "i".
Примечание Все функции работы с комплексными числами допускают обозначение для мнимой единицы "i" или "j", но не "I" или "J". Использование верхнего регистра приводит к получению значения ошибки #ЗНАЧ!. Все функции, которые используют два или больше комплексных числа, требуют, чтобы обозначение мнимой единицы было одно и то же.
Замечания
Если действительная_часть не число, то функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
Если мнимая_часть не число, то функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
Если мнимая_единица ни "i" ни "j", то функция КОМПЛЕКСН возвращает значение ошибки #ЗНАЧ!.
Примеры
КОМПЛЕКСН(3;4) равняется 3 + 4i
КОМПЛЕКСН(3;4;"j") равняется 3 + 4j
КОМПЛЕКСН(0;1) равняется i
КОМПЛЕКСН(1;0) равняется 1
МНИМ.ABS
Возвращает абсолютную величину (модуль) комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.ABS (компл_число)
Компл_число - это комплексное число, для которого находится абсолютная величина.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.ABS возвращает значение ошибки #ЧИСЛО!.
Абсолютная величина комплексного числа определяется следующим образом:


где:
z = x + yi
Пример
МНИМ.ABS("5+12i") равняется 13
МНИМ.ВЕЩ
Возвращает коэффициент при вещественной части комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.ВЕЩ (компл_число)
Компл_число - это комплексное число, для которого определяется коэффициент при вещественной (действительной) части.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.ВЕЩ возвращает значение ошибки #ЧИСЛО!.
Пример
МНИМ.ВЕЩ("6-9i") равняется 6
МНИМ.COS
Возвращает косинус комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.COS (компл_число)
Компл_число - это комплексное число, для которого определяется косинус.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не текст, то функция МНИМ.COS возвращает значение ошибки #ЗНАЧ!.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.COS возвращает значение ошибки #ЧИСЛО!.
Косинус комплексного числа определяется следующим образом:


Пример
МНИМ.COS("1+i") равняется 0,83373 - 0,988898i
МНИМ.EXP
Возвращает экспоненту комплексного числа в формате x + yi или x + yj.
Если эта функция недоступна, следует установить надстройку "Пакет анализа", а
Синтаксис
МНИМ.EXP (компл_число)
Компл_число - это комплексное число, для которого определяется экспонента.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.EXP возвращает значение ошибки #ЧИСЛО!.
Экспонента комплексного числа определяется следующим образом:


Пример
МНИМ.EXP("1+i") равняется 1,468694 + 2,287355i
МНИМ.LN
Возвращает натуральный логарифм комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.LN (компл_число)
Компл_число - это комплексное число, для которого определяется натуральный логарифм.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.LN возвращает значение ошибки #ЧИСЛО!.
Натуральный логарифм комплексного числа определяется следующим образом:



Пример
МНИМ.LN("3+4i") равняется 1,609438 + 0,927295i
МНИМ.LOG10
Возвращает обычный логарифм (десятичный) комплексного числа, представленного в формате x + yi или x + yj.
Синтаксис
МНИМ.LOG10 (компл_число)
Компл_число - это комплексное число, для которого определяется обычный логарифм.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.LOG10 возвращает значение ошибки #ЧИСЛО!.
Обычный логарифм комплексного числа может быть вычислен через натуральный логарифм следующим образом:


Пример
МНИМ.LOG10("3+4i") равняется 0,69897 + 0,402719i
МНИМ.LOG2
Возвращает двоичный логарифм комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.LOG2 (компл_число)
Компл_число - это комплексное число, для которого определяется двоичный логарифм.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.LOG2 возвращает значение ошибки #ЧИСЛО!.
Двоичный логарифм комплексного числа может быть вычислен через натуральный логарифм следующим образом:


Пример
МНИМ.LOG2("3+4i") равняется 2,321928 + 1,337804i
МНИМ.SIN
Возвращает синус комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.SIN (компл_число)
Компл_число - это комплексное число, для которого определяется синус.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.SIN возвращает значение ошибки #ЧИСЛО!.
Синус комплексного числа определяется следующим образом:


Пример
МНИМ.SIN("3+4i") равняется 3,853738 - 27,016813i
МНИМ.АРГУМЕНТ
Возвращает значение аргумента комплексного числа  , то есть угол, выраженный в радианах, который определяется следующим образом:
, то есть угол, выраженный в радианах, который определяется следующим образом:


Синтаксис
МНИМ.АРГУМЕНТ (компл_число)
Компл_число— это комплексное число, для которого определяется аргумент  .
.
Замечания
Для преобразования коэффициентов при действительной и мнимой части в комплексное число используйте функцию КОМПЛЕКСН.
Если компл_число представлено не в форме x + yi или x + yj, то функция МНИМ.АРГУМЕНТ возвращает значение ошибки #ЧИСЛО!.
МНИМ.АРГУМЕНТ вычисляется следующим образом:


где:

 и
и
z = x + yi
Пример
МНИМ.АРГУМЕНТ("3+4i") равняется 0,927295
МНИМ.ДЕЛ
Возвращает частное от деления двух комплексных чисел в формате x + yi или x + yj.
Синтаксис
МНИМ.ДЕЛ (компл_число1; компл_число2)
Компл_число1 - это комплексный числитель или делимое.
Компл_число2 - это комплексный знаменатель или делитель.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число1 или компл_число2 не представлено в форме x + yi или x + yj, то функция МНИМ.ДЕЛ возвращает значение ошибки #ЧИСЛО!.
Частное двух комплексных чисел определяется следующим образом:


Пример
МНИМ.ДЕЛ("-238+240i";"10+24i") равняется 5 + 12i
МНИМ.КОРЕНЬ
Возвращает значение квадратного корня комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.КОРЕНЬ (компл_число)
Компл_число - это комплексное число, для которого определяется квадратный корень.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.КОРЕНЬ возвращает значение ошибки #ЧИСЛО!.
Квадратный корень комплексного числа определяется следующим образом:


где:

и:

и:


Пример
МНИМ.КОРЕНЬ("1+i") равняется 1,098684 + 0,45509i
МНИМ.ПРОИЗВЕД
Возвращает произведение от 2 до 29 комплексных чисел в формате x + yi или x + yj.
Синтаксис
МНИМ.ПРОИЗВЕД (компл_число1; компл_число2;...)
Компл_число1, компл_число2 - это от 1 до 29 перемножаемых комплексных чисел.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число1 или компл_число2 не представлено в форме x + yi или x + yj, то функция МНИМ.ПРОИЗВЕД возвращает значение ошибки #ЧИСЛО!.
Произведение двух комплексных чисел определяется следующим образом:


Примеры
МНИМ.ПРОИЗВЕД("3+4i";"5-3i") равняется 27 + 11i
МНИМ.ПРОИЗВЕД("1+2i";30) равняется 30 + 60i
МНИМ.РАЗН
Возвращает разность двух комплексных чисел в формате x + yi или x + yj.
Синтаксис
МНИМ.РАЗН (компл_число1; компл_число2)
Компл_число1 - это уменьшаемое комплексное число.
Компл_число2 - это вычитаемое комплексное число.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если любое из комплексных чисел не представлено в форме x + yi или x + yj, то функция МНИМ.РАЗН возвращает значение ошибки #ЧИСЛО!.
Разность двух комплексных чисел определяется следующим образом:


Пример
МНИМ.РАЗН("13+4i";"5+3i") равняется 8 + i
МНИМ.СОПРЯЖ
Возвращает комплексно-сопряженное комплексное число в формате x + yi или x + yj.
Синтаксис
МНИМ.СОПРЯЖ (компл_число)
Компл_число - это комплексное число, для которого определяется сопряженное комплексное число.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.СОПРЯЖ возвращает значение ошибки #ЧИСЛО!.
Сопряженное комплексное число определяется следующим образом:


Пример
МНИМ.СОПРЯЖ("3+4i") равняется 3 - 4i
МНИМ.СТЕПЕНЬ
Возвращает комплексное число в формате x + yi или x + yj возведенное в степень.
Синтаксис
МНИМ.СТЕПЕНЬ (компл_число; число)
Компл_число - это комплексное число, возводимое в степень.
Число - это степень, в которую возводится комплексное число.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.СТЕПЕНЬ возвращает значение ошибки #ЧИСЛО!.
Если аргумент число не является числом, то функция МНИМ.СТЕПЕНЬ возвращает значение ошибки #ЗНАЧ!.
Число может быть целым, дробным или отрицательным.
Комплексное число возведенное в степень вычисляется следующим образом:


где:


и:


и:


Пример
МНИМ.СТЕПЕНЬ("2+3i"; 3) равняется -46 + 9i
МНИМ.СУММ
Возвращает сумму двух или более комплексных чисел в формате x + yi или x + yj.
Синтаксис
МНИМ.СУММ (компл_число1;компл_число2;...)
Компл_число1, компл_число2,... - это от 1 до 29 суммируемых комплексных чисел.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если любое из комплексных чисел не представлено в форме x + yi или x + yj, то функция МНИМ.СУММ возвращает значение ошибки #ЧИСЛО!.
Сумма двух комплексных чисел определяется следующим образом:


Пример
МНИМ.СУММ("3+4i";"5-3i") равняется 8 + i
МНИМ.ЧАСТЬ
Возвращает коэффициент при мнимой части комплексного числа в формате x + yi или x + yj.
Синтаксис
МНИМ.ЧАСТЬ (компл_число)
Компл_число - это комплексное число, для которого определяется коэффициент при мнимой части.
Замечания
Функция КОМПЛЕКСН используется для преобразования коэффициентов при действительной и мнимой части в комплексное число.
Если компл_число не представлено в форме x + yi или x + yj, то функция МНИМ.ЧАСТЬ возвращает значение ошибки #ЧИСЛО!.
Примеры
МНИМ.ЧАСТЬ("3+4i") равняется 4
МНИМ.ЧАСТЬ("0-j") равняется -1
МНИМ.ЧАСТЬ(4) равняется 0
БЕССЕЛЬ.I
Возвращает модифицированную функцию Бесселя, что эквивалентно вычислению функции Бесселя для чисто мнимого аргумента.
Если эта функция недоступна, следует установить надстройку "Пакет анализа", а затем подключить ее с помощью команды Надстройки меню Сервис.
Синтаксис
БЕССЕЛЬ.I (x; n), где
X - это значение, для которого вычисляется функция.
N - это порядок функции Бесселя. Если n не целое, то производится усечение.
Замечания
Если x не число, то БЕССЕЛЬ.I возвращает значение ошибки #ЗНАЧ!.
Если n не число, то БЕССЕЛЬ.I возвращает значение ошибки #ЗНАЧ!.
Если n < 0, то БЕССЕЛЬ.I возвращает значение ошибки #ЧИСЛО!.
Модифицированная функция Бесселя порядка n от переменной x это:
 Пример
Пример
БЕССЕЛЬ.I(1,5; 1) равняется 0,981666
БЕССЕЛЬ.J
Возвращает функцию Бесселя.
Если эта функция недоступна, следует установить надстройку "Пакет анализа", а затем подключить ее с помощью команды Надстройки меню Сервис.
Инструкции
Синтаксис
БЕССЕЛЬ.J (x; n)
X - это значение, для которого вычисляется функция.
N - это порядок функции Бесселя. Если n не целое, то производится усечение.
Замечания
Если x не число, то БЕССЕЛЬ.J возвращает значение ошибки #ЗНАЧ!.
Если n не число, то БЕССЕЛЬ.J возвращает значение ошибки #ЗНАЧ!.
Если n < 0, то БЕССЕЛЬ.J возвращает значение ошибки #ЧИСЛО!.
Функция Бесселя порядка n от переменной x это:


Пример
БЕССЕЛЬ.J(1,9; 2) равняется 0,329926
БЕССЕЛЬ.K
См. также
Возвращает модифицированную функцию Бесселя, что эквивалентно вычислению функции Бесселя для чисто мнимого аргумента.
Если эта функция недоступна, следует установить надстройку "Пакет анализа", а затем подключить ее с помощью команды Надстройки меню Сервис.
Инструкции
Синтаксис
БЕССЕЛЬ.K (x; n)
X - это значение, для которого вычисляется функция.
N - это порядок функции. Если n не целое, то производится усечение.
Замечания
Если x не число, то БЕССЕЛЬ.K возвращает значение ошибки #ЗНАЧ!.
Если n не число, то БЕССЕЛЬ.K возвращает значение ошибки #ЗНАЧ!.
Если n < 0, БЕССЕЛЬ.K возвращает значение ошибки #ЧИСЛО!.
Модифицированная функция Бесселя порядка n от переменной x это:

 ,
,
где Jn и Yn являются функциями Бесселя J и Y соответственно.
Пример
БЕССЕЛЬ.K(1,5; 1) равняется 0,277388
БЕССЕЛЬ.Y
См. также
Возвращает функцию Бесселя, которая также называется функцией Вебера или функцией Неймана.
Если эта функция недоступна, следует установить надстройку "Пакет анализа", а затем подключить ее с помощью команды Надстройки меню Сервис.
Инструкции
Синтаксис
БЕССЕЛЬ.Y (x; n)
X - это значение, для которого вычисляется функция.
N - это порядок функции. Если n не целое, то производится усечение.
Замечания
Если x не число, то БЕССЕЛЬ.Y возвращает значение ошибки #ЗНАЧ!.
Если n не число, то БЕССЕЛЬ.Y возвращает значение ошибки #ЗНАЧ!.
Если n < 0, БЕССЕЛЬ.Y возвращает значение ошибки #ЧИСЛО!.
Функция Бесселя порядка n от переменной x это:
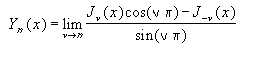
Пример
БЕССЕЛЬ.Y(2,5; 1) равняется 0,145918
Инженерные функции пакета «Анализ» для преобразования чисел из одной системы счисления в другую






