Вариант1 Часть1
Модуль «Алгебра»
В1. Вычислите 
А1. Какое из неравенств верно для числа, отмеченного на координатной прямой точкой А?
1)А<√5 2)А≤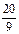 
3)А≥ 
4) √17<А
А2. На каком из рисунков изображено решение неравенства х2≤ х+6?
В2. Решите уравнение (5-х)2=3х(5-х). Если уравнение имеет несколько корней, в
ответ запишите больший корень.
В3. Найдите значение выражения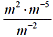 
при m=0,2.
В4. Дана арифметическая прогрессия 12; 9,3; 6,6.… Найти сумму шести первых её членов.
А3. Разложите на множители квадратный трехчлен 2y2-7y+6.
В5. Установите соответствие между графиками функций и формулами, которые их задают. В ответе запишите последовательность чисел без пробелов и запятых, в указанном порядке.
Модуль «Геометрия»
В6. Разность углов, прилежащих к одной стороне параллелограмма равна 48° Найдите больший угол параллелограмма. Ответ дайте в градусах
В7. В окружности с центром в точке О проведены диаметры AD и ВС, Найдите величину угла 
ОАВ, если OCD=350
В8. Основания трапеции 8 см и 14 см. Диагональ трапеции делит среднюю
линию на два отрезка. Найдите больший из них.
В9. Найдите площадь фигуры, изображенной на рисунке, если стороны
квадратных клеток равны 1.
В10. Укажите номера верных утверждений.
1. Если в параллелограмм можно вписать окружность, то этот параллелограмм – ромб;
2. Если две медианы треугольника равны, то он равносторонний;
3. Если около ромба описана окружность, то этот ромб – квадрат.
Модуль «Реальная математика»
А4. В таблице приведены нормативы по бегу на лыжах на 1 км для 10 класса.
Какую отметку получит девочка, пробежавшая на лыжах 1 км за 6 минут 15 секунд?
1) Неудовлетворительно
2) «4»
3) «3»
4) «5»
В11
В12. В цирке для продажи было заготовлено некоторое количество шариков.
Перед началом представления было продано 40% всех воздушных шариков, а
в антракте – еще 12 штук. После этого осталась половина всех шариков.
Сколько шариков было первоначально?
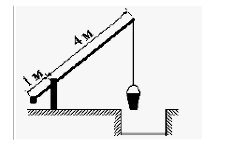
В13. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а
длинное плечо 4 м. На сколько метров опустится конец длинного плеча, когда конец
короткого поднимется на 0,5м?
В14. 156 учащимся восьмых классов некоторой школы была предложена контрольная работа по алгебре из 5 заданий. По результатам составили таблицу1, в которой указали число учащихся, выполнивших одно, два три и т.д. заданий:
(таблица1) (таблица2)
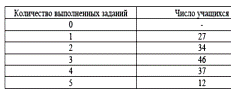
Сколько человек получили оценку не ниже «3», если критерии выставления оценок определялись по таблице 2?
В15. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру будет не Петя.
В16. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях) рассчитывается по формуле C=150+11· (t−5), где t-длительность поездки, выраженная в минутах (t>5). Пользуясь этой формулой, рассчитайте стоимость 15-минутной поездки.
Вариант1 Часть2
Модуль «Алгебра»
С1. Решите систему
С2. На тренировке по картингу один карт проходил круг на 10 секунд медленнее другого и через минуту отстал от него ровно на круг. За сколько секунд каждый карт проходил круг?
С3. 
Модуль «Геометрия
Вариант 2 Часть1
Модуль «Алгебра»
В1. Вычислите 
А1. Какое из неравенств верно для числа а, отмеченного на координатной прямой?
1)а>√10 2)а≤ 
3)а≥ 
4) а<√3
А2. На каком из рисунков изображено решение неравенства х2≥ х+6?
В2. Решите уравнение (3+х)2=5х(3+х) Если уравнение имеет несколько корней, в
ответ запишите меньший корень.
В3. Найдите значение выражения 
при n=0,1.
В4. Дана арифметическая прогрессия -12; -9,3; -6,6…Найдите сумму первых шести ее членов.
А3. Разложите на множители многочлен2y2-5y+3
1)(y-1)(y+1,5) 3) (y-1)(2y-3)
2) 2(y-1)(y+1,5) 4)(y-1)(2y-3)
В5. Установите соответствие между графиками функций и формулами, которые их задают. В ответе запишите последовательность чисел без пробелов и запятых, в указанном порядке.
Модуль «Геометрия»
В6. Сумма двух углов равнобедренной трапеции равна 150o. Найдите больший угол трапеции.
В7. Угол АСО равен 28°. Его сторона СА касается окружности с центром в точке О. Найдите градусную величину дуги АВ окружности, заключенной внутри этого угла
В8. Высота трапеции равна 10 см. Площадь трапеции равна 150 см2. Найдите
среднюю линию этой трапеции.
В9. Найдите синус угла АВС, изображенного на рисунке
В10. Укажите номера верных утверждений.
1. Биссектрисы смежных углов взаимно перпендикулярны;
2. Если в параллелограмме две высоты равны, то этот параллелограмм – ромб;
3. Медианой треугольника называется отрезок, соединяющий вершину треугольника с точкой на противоположной стороне.
Модуль «Реальная математика»
А4. В таблице приведены нормативы по бегу на лыжах на 1 км для 10 класса.
Какую отметку получит мальчик, пробежавший на лыжах 1 км за 4 минуты 45 секунд?
1) Неудовлетворительно 2) «4» 3) «3» 4) «5»
В11
В12. В цирке для продажи было заготовлено некоторое количество шариков. Перед началом представления было продано 20% всех воздушных шариков, а в антракте – еще 57 штук. После этого осталась половина всех шариков. Сколько шариков было первоначально?
В13. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо 4 м. На сколько метров поднимется конец короткого плеча, когда конец длинного опустится на 2 м?
В14. 156 учащимся восьмых классов некоторой школы была предложена контрольная работа по алгебре из 5 заданий. По результатам составили таблицу1, в которой указали число учащихся, выполнивших одно, два три и т.д. заданий:
(таблица1) (таблица2)
Сколько человек получили оценку не выше «3», если критерии выставления оценок определялись по таблице 2?
В15. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
В16. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6500+4000·n, где n —число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец.
Вариант2 Часть2
Модуль «Алгебра»
С1. Решите систему
С2. На соревнованиях по кольцевой трассе один лыжник проходил круг на 3 мин быстрее другого и через час обогнал его ровно на круг. За сколько минут каждый лыжник проходил круг?
