МАТЕМАТИКА
1. 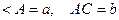 болатын АВС тең бүйірлі
болатын АВС тең бүйірлі 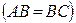 үшбұрыштың АЕ биссектрисасын табыңыз. (
үшбұрыштың АЕ биссектрисасын табыңыз. (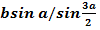 )
)
2. А бұрышы тік, АВС тең бүйірлі үшбұрышының АС катетінде К нүктесі берілген. 5АК=АВ болса, К нүктесі АС катетін қандай қатынаста бөледі. (1:4)
3. А бұрышының биссектрисасы ВС қабырғасын 45,6см мен 7,85см кесінділерге бөлетін АВСD тік төртбұрыштың периметрін табыңыз (198,1;122,6).
4. A(1;2) B(7;10) АВ кесіндісін 1:3 қатынасында бөлетін нүктенінің координатасын табыңыз. (2.5;4)
5. 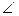 А=300, ВС=6 болатын АВС тік бұрышты үшбұрышқа сырттай сызылған шеңбердің радиусын тап. (6)
А=300, ВС=6 болатын АВС тік бұрышты үшбұрышқа сырттай сызылған шеңбердің радиусын тап. (6)
6. 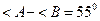 болатын параллелограммның бұрыштарын т/з (62030 мен 117030)
болатын параллелограммның бұрыштарын т/з (62030 мен 117030)
7. А(-1;1), В(1;0) нүктелері арқылы өтетін 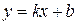 түріндегі түзудің теңдеуін құр: (y= –
түріндегі түзудің теңдеуін құр: (y= – 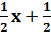 )
)
8. А(1;3;-2), В(-5;7;8) нүктелері берілген. М нүктесі АВ кесіндісінің ортасы болса, М нүктесінің координаттарын тап. (М(-2;5;3)
9. А(–1;6;2),В(3;а;4) нүктелерiнің координаттары берiлген. а-ның қандай мәнінде АВ векторының ұзындығы 2  -ке тең. (6)
-ке тең. (6)
10. А(х;2;3), В(1;3;у) нүктелері және 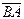 (4;-1;-3)-ке тең. х пен у-ті т/з.(х=5;у=6)
(4;-1;-3)-ке тең. х пен у-ті т/з.(х=5;у=6)
11. A(3;-1), B(-5;4) нүктелерінен бірдей қашықтықтағы сызықтың теңдеуін көрсет:(16x-10y+31=0)
12. А(14; -8;-1), В(7; 3; -1), C(-6; 4;-1) АВСD ромбысының төбелері болса, ромбтың сүйір бұрышын табыңыз. (arccos 3/5)
13. A(2;0;0), B(0;0;0), C(0;2;0), B1(0;0;2) ABCA1B1C1 призмасының төбелері. С1 нүктесінің координатасын табыңыз. (0;2;2)
14. A(2;0;0), B(0;0;0), C(0;2;0), B1(0;0;2) ABCA1B1C1 призмасының төбелері 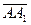 векторының координатасын табыңыз. (0;0;2)
векторының координатасын табыңыз. (0;0;2)
15. A(2;0;0;), B(0;0;0), C(0;2;0), B1(0;0;2) ABCDA1B1C1D1 кубының төбелері болса, С1 нүктесінің координаталарын табыңыз. (0;2;2)
16. A(2;0;0;), B(0;0;0), C(0;2;0), B1(0;0;2) ABCDA1B1C1D1 кубының төбелері болса,С1D векторының координатасын табыңыз. (2;0;-2)
17. A(1;2), B(2;3), C(-1;4), D(3;-2) болса, 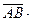
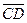 скаляр көбейтіндісін тап. (-2)
скаляр көбейтіндісін тап. (-2)
18. A(1;2), B(2;3), C(-1;4), D(3;-2) болса, (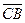 +
+ 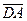 )(
)(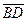 –
– 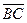 ) скаляр көбейтіндісін табыңыз. (-14)
) скаляр көбейтіндісін табыңыз. (-14)
19. А(1;2),В(2;3),С(-1;4),D(3;-2) болса, 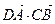 скаляр көбейтіндісін табыңыз. (-10)
скаляр көбейтіндісін табыңыз. (-10)
20. A(3;-2;4), B(4;-1;2), C(6;-3;2), D(7;-3;1) нүктелері берілген.  және
және 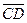 векторларының арасындағы бұрыш неге тең? (300)
векторларының арасындағы бұрыш неге тең? (300)
21. A(5;-8;-1), B(6;-8;-2), C(7;-5;-11), D(7;-7;-9) нүктелері берілген.  және
және 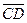 векторларының арасындағы бұрыш неге тең? (1200)
векторларының арасындағы бұрыш неге тең? (1200)
22. А(1;-1;-4),В(-3;-1;0), С(-1;2;5), Д(2;-3;1) нүктелерiнiң координаттары берiлген. АВ және СД векторларының арасындағы бұрыштың косинусын тап. (-0,7)
23. А(-3;2;-1), В(2;-1;-3), С(1;-4;3), Д(-1;2;-2) нүктелерінің координаттары берілген. 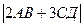 табыңыз. (
табыңыз. ( )
)
24. А,В,С нүктелері центірі О шеңберінде орналасқан. АВС=500. АВ және СВ хордалары қатынасы 5:8 болса АВ хордасын тап. (1000)
25. А,В,С нүкелері центрі О болатын шеңберде жатыр. АОС бұр-шы 1460 – қа тең. В және О нүктелері АС түзуінен бір жақта жатқанда АВС бұрышын табыңдар (730)
26. А(1;2;3),В(6;3;6), С(-2;5;2) нүктелерi берiлген. АВС үшбұрышының медианасы АК-ның үзындығын табыңыз. (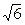 )
)
27. А(1;3), В(5;-7), С(-1;9) төбелері болатын АВС үшбұрышының АМ медианасы жататын түзудің теңдеуін тап. (у=-2x+5)
28. А(1;3), В(5;-7), С(-1;9) төбелері болатын АВС үшбұрышының ВМ медианасы жататын түзудің теңдеуін тап. (5у+13х-30=0)
29. А(1;0;3), В(1;1;-3), С(3;1;-1) төбелері болатындай үшбұрыштың АК медианасының ұзындығын тап. (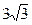 )
)
30. А(-1; -2; 4), В(-4; -2; 0), С(3; -2; 1) үшбұрышының төбелері болса, А төбесіндегі үшбұрыштың бұрышын табыңыз. (900)
31. А(2;-3;2), В(3;-3;2), С(2;-1;2) төбелері бар үшбұртың периметрін т/з (3+ 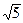 )
)
32. А(3; -1;1),В(1;-1;3),С(3;1;-1) үшбұрыштың төбелері болса, 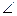 АВС бұрышын тап.(300)
АВС бұрышын тап.(300)
33. А(9;3;-5),В(2;10;-5),С(2;3;2) төбелері бар үшбұрышының ауданын тап: (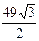 )
)
34. А және В, АВ кесіндісінің ортасы М нүктелері A1 В1 М1нүктелеріне кескінделген, Егер AA1=3см, BB1=7см болса, онда ММ1 кесіндісінің ұзындығы неге тең?(5;2)
35. А және В, АВ кесіндісінің ортасы М нүктелері A1 В1 М1нүктелеріне кескінделген, Егер AA1=3см, BB1=2см болса, онда ВВ1 кесіндісінің ұзындығы неге тең?(1;7)
36. A(0;2) және B(3;0) берілсе АM=ВМ теңдігі орындалатын М(х;у) нүктелерінің жиынын көрсетіңіз. (6x-4y=5)
37. A(0;2) және B(3;0) берілсе, АМ2+ВМ2=2AB2 теңдігі орындалатын М(х;у) нүктелерінің жиынын көрсетіңіз. ((x-1.5)2+(y-1)2=9.75)
38. A(0;2) және B(3;0) берілсе, АМ2–ВМ2=AB2 теңдігі орындалатын М(х;у) нүктелерінің жиынын көрсетіңіз. (3x-2y=9)
39. А(1;2) және В(0;0) В нүк-і АС кесіндісінің ортасы болса, С нүктесінің координатасын табыңыз. (-1;-2)
40. A(1;3) және В(3;1) кесіндінің ұштары болса, ортасының координатасын т/з. (2;2)
41. А(1;-1) ж/е В(2;3) нүк-рі арқылы өтетін түзудің бұрыштық коэффициентін тап.(4)
42. А(–1;1) және В(1;0) нүктелері арқылы өтетін түзудің теңдеуін жаз.(x 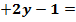 0)
0)
43. А(–1;1) және В(2;5) нүктелері арқылы өтетін түзудің теңдеуін жаз. (4 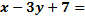 0)
0)
44. A(3;-1) және В(1;-4) нүктелері берілген, 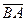 векторының ұзындығы.(
векторының ұзындығы.( )
)
45. A(5;3) және В(2;-1) нүктелері берілген, 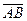 векторының ұзындығы.(5)
векторының ұзындығы.(5)
46. A(0;1) және В(1;-1) нүктелері берілген. 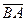 векторының координатасы,(- 1;2)
векторының координатасы,(- 1;2)
47. A(-1;0) және В(1;-1) нүктелері берілген, 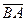 векторының координатасы ,(-2;1)
векторының координатасы ,(-2;1)
48. A(1;1) және В(-1;1) нүктелерінің арақашықтығы. (2)
49. A(-1;-1) және В(-1;1) нүктелерінің ара қашықтығы (2)
50. A(6;7;8) және В(-8;2;6) нүктелерінің ара қашықтығы (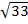 )
)
51. А және В нүктелері шеңберді екі доғаға бөледі. Оның кішісі 1400-қа тең, ал үлкенін N нүктесі А нүктесінен бастап санағанда 6:5 етіп бөледі. ВАN бұрышын тап. (500).
52. А және В пункттерінен бір мезгілде бір-біріне қарама- қарсы екі автомобиль шықты. Екеуі кездескеннен кейін олардың біреуі В пунктіне 1с15мин –н соң, ал екіншісі А пунктіне 48м-тан соң келіп жетті. А және В пунктерінің ара қашық-тығы 90км. Автомобильдің әрқайсысының жылдамдығын т/з. (40; 50км/ сағ)
53. А және В пунктерінен бір мезгілде бір-біріне қарсы мотоциклші мен велосипед-ші шықты. Олар В пунктінен 4 км қашықтықта кездесті. Ал мотоциклші В пункті-не жеткен кезде велосипедші А пунктінен 15 км қашықтықта еді. А және В пунктерінің ара қашықтығын табыңыз. (20км)
54. А және В станцияларының арасын жүк поезына қарағанда жолаушы поезы 36 мин тезірек жүріп өтеді. Егер жолаушы поезының орташа жылдамдығы 60 км/сағ, ал жүк поезының орташа жылдамдығы 48 км/сағ болса, онда екі станцияның ара қашықтығын табыңыз. (144км)
55. А нүктесі арқылы АВ жанамасы (В–жанасу нүктесі), және 0 центрі арқылы өтетін, шеңберді С және Д нүтелерінде қиятын қиюшы жүргізілген АВ=4cм, AC=2см деп лып СД 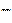 ны тап .(6см)
ны тап .(6см)
56. А(5;12) нүктесі арқылы өтетін, центрі координаттар басында болатын шеңбердің теңдеуін тап. 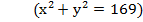 .
.
57. А(9,3) нүктесі арқылы өтетін ж/е Ох осіне перпендикуляр болатын түзудің теңдеуін табыңыз. (x=9)
58. А нүктесі жазықтықтан 18 см қашықтықта жатыр. Осы нүктеден өтетін және жазықтықпен 600 бұрыш жасайтын көлбеудің ұзындығын табыңыз. (12 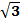 см)
см)
59. А нүктесі y= 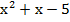 функциясының графигіне тиісті. Осы нүктеде функцияға жүргізілген жанаманың Ох осімен жасайтын бұрышының тангенсі 5-ке тең. А нүктесінің абциссасын табыңыз. (2).
функциясының графигіне тиісті. Осы нүктеде функцияға жүргізілген жанаманың Ох осімен жасайтын бұрышының тангенсі 5-ке тең. А нүктесінің абциссасын табыңыз. (2).
60. А нүктесінде тұрған ит өзінен 30 м жерде тұрған түлкіні қуды. Ит бір секіргенде 2 м, ал түлкі бір секіргенде 1 м жерге барады. Түлкі үш рет секірген уақытта ит екі рет секіреді. Ит А нүктесінен қандай қашықтықта түлкіні қуып жетеді? (120 м)
61. A(10;0;0) нүктесінен B(0;0;0),C(8;6;0;) нүктелерін басып өтетін түзуге дейінгі қашықтықты табыңыз. (6)
62. A(1;2) нүктесінен және координат басынан бірдей қашықтықтағы абцисса осіндегі нүктенінің координатасын табыңыз. (2.5;0)
63. А(3;-2;-4) нүктесінен ОУ осіне дейінгі және А нүк-н XOZ жазықтығына дейінгі ара қашықтықтарының қосындысын табыңыз (7)
64. А(3;-4) нүктесінен өтетін, центрі координаттар басында орналасқан шеңбердің теңдеуін көрсетіңіз (х2+у2=25)
65. А нүктесінен центрі О нүктесі болатын шеңберге АС жанама жүргүзілген. ОА кесінді 20, ал ОС кесінді 16 болса, онда СА кесіндісінің ұзындығын тап. (12см).
66. 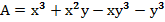 өрнегінің x= 3,6; y= –2,6 болғандағы сан мәнін тап. (6,2)
өрнегінің x= 3,6; y= –2,6 болғандағы сан мәнін тап. (6,2)
67. А пунктінен өзен ағысымен сал жіберілгеннен кейін 5 сағат 20 минут өткен соң салдың соңынан моторлы қайық шығып, 20км жүзгеннен кейін салды қуып жетеді.Егер моторлы қайық салдан 12 км / сағ жылдам жүретін болса, салдың жылдамдығы неге тең? (3 км / сағ)
68. 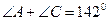 болатын параллелограммның бұрыштарын т/з. (710 мен 1090)
болатын параллелограммның бұрыштарын т/з. (710 мен 1090)
69. А(2;5;-3),С(10;5;5),D(3;6;4) нүктелері ABCD ромбының төбелері. BD диагоналінің ұзындығын табыңыз (2 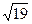 )
)
70. a> 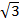 , болса онда
, болса онда 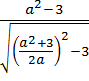 өрнегінің ықшамдалған түрін табыңыз. (2)
өрнегінің ықшамдалған түрін табыңыз. (2)
71. 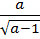 бөлшектің бөліміндегі иррационалдықтан құтылыңыз. (
бөлшектің бөліміндегі иррационалдықтан құтылыңыз. (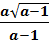 )
)
72. 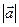 =2,
=2, 
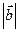 =3, арасындағы бұрышы 1200 болса, (2
=3, арасындағы бұрышы 1200 болса, (2 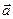 +3
+3 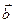 )(
)(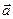 –
– 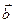 ) скаляр көбейтіндісін табыңыз. (-22)
) скаляр көбейтіндісін табыңыз. (-22)
73. 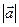 =3,
=3, 
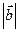 =2 болса,
=2 болса, 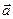 +
+ 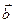 және
және 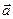 –
– 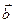 векторларының скаляр көбейтіндісін табыңыз. (5)
векторларының скаляр көбейтіндісін табыңыз. (5)
74. 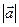 =3,
=3, 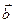 векторының
векторының 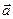 векторына проекциясы 2-ге тең болса,
векторына проекциясы 2-ге тең болса, 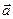 және
және 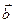 векторларының скаляр көбейтіндісін табыңыз. (±6)
векторларының скаляр көбейтіндісін табыңыз. (±6)
75. 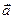 {1;6},
{1;6}, 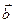 {-5;7} болса,
{-5;7} болса, 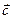 =2
=2 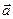 +
+ 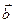 векторын табыңыз. {-3;19 }
векторын табыңыз. {-3;19 }
76. 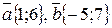 болса
болса 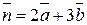 векторын табыңыз {-3;19 }
векторын табыңыз {-3;19 }
77. 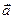 {1;6},
{1;6}, 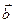 {-5;7} болса,
{-5;7} болса, 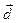 =
= 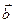 -
- 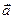 векторын табыңыз. {-6;1}
векторын табыңыз. {-6;1}
78. 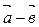 және
және 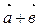 векторларының арасындағы бұрыштың косинусын тап, егер
векторларының арасындағы бұрыштың косинусын тап, егер 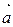 (1;2;1) және
(1;2;1) және 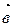 (2;-1;0) (1/11)
(2;-1;0) (1/11)
79. a, bжәне c сандары айырымыd=4 болатын арифметикалық прогрессияны құрайды. Егер a; b; c+8 сандары геометриялық прогрессияның тізбектес мүшелері болса, онда a,b.c сандарын табыңыз. (a=2; b=6; c=10)
80. 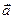 {1;4}
{1;4} 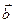 {1;2}
{1;2} 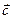 {7;2} болса,
{7;2} болса, 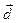 =3
=3 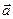 –2
–2 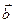 +
+ 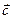 векторын табыңыз. {8;10}
векторын табыңыз. {8;10}
81. 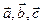 векторлары келесі шарттарды қанағаттандырады
векторлары келесі шарттарды қанағаттандырады 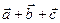 =0
=0 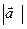 =1,
=1, 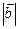 =4,
=4, 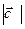 =5. Есепте.
=5. Есепте. 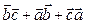 . (- 21)
. (- 21)
82. 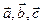 векторлары келесі шарттарды қанағаттандырады
векторлары келесі шарттарды қанағаттандырады 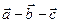 =0,
=0, 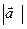 =3,
=3, 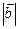 =4,
=4, 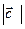 =5. Есепте.
=5. Есепте. 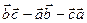 . (- 25)
. (- 25)
83. 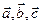 векторлары өзара перпендикуляр.
векторлары өзара перпендикуляр. 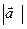 =y болса,
=y болса, 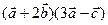 скаляр көбейтіндісін анықтаңыз. (3y2)
скаляр көбейтіндісін анықтаңыз. (3y2)
84. 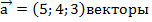 мен 0х осі арасындағы бұрышты есептеңіз. (
мен 0х осі арасындағы бұрышты есептеңіз. ( 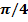 )
)
85. 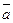 векторы Ох осімен оң бағытта 1350 жасайды. Егер
векторы Ох осімен оң бағытта 1350 жасайды. Егер 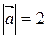 болса,
болса, 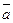 векторының абциссасын табыңыз (
векторының абциссасын табыңыз (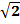 )
)
86. 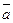 векторы Оу осімен оң бағытта 1500 жасайды. Егер
векторы Оу осімен оң бағытта 1500 жасайды. Егер 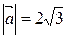 болса,
болса, 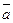 векторының ординатасын табыңыз (-3)
векторының ординатасын табыңыз (-3)
87. 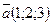 векторын
векторын 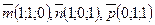 векторлары арқылы жіктеңіз
векторлары арқылы жіктеңіз 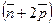
88. 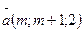 векторының ұзындығы үштен кем болатындай m–ның барлықмәнін табыңыз (-2;1)
векторының ұзындығы үштен кем болатындай m–ның барлықмәнін табыңыз (-2;1)
89. 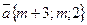 векторының ұзындығы үштен кем болатындай m–ның барлықмәнін табыңыз [- 2;1 ]
векторының ұзындығы үштен кем болатындай m–ның барлықмәнін табыңыз [- 2;1 ]
90. 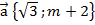 векторының ұзындығы 8-ден аспайтындай m-ның барлық мәндер жиынын көрсет.
векторының ұзындығы 8-ден аспайтындай m-ның барлық мәндер жиынын көрсет. 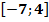
91. 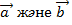 айқас түзулер берілген, біреуі а түзуі, екіншісі b түзуі арқылы өтетін өзара перпендикуляр қанша жазықтық жүргізуге болады (жалғыз)
айқас түзулер берілген, біреуі а түзуі, екіншісі b түзуі арқылы өтетін өзара перпендикуляр қанша жазықтық жүргізуге болады (жалғыз)
92. 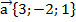 және
және 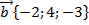 берілген болса, онда
берілген болса, онда 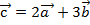 векторының ұзындығын табыңыз.
векторының ұзындығын табыңыз. 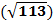
93. 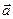 және
және 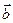 бірлік векторларының арасындағы бұрыш 60 0,
бірлік векторларының арасындағы бұрыш 60 0, 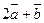 векторының ұзындығы неге тең
векторының ұзындығы неге тең 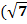 )
)
94. 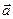 =3
=3 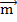 +2
+2 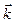 және
және 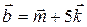 векторлар арасындағы бұрышты табыңыз, мұндағы
векторлар арасындағы бұрышты табыңыз, мұндағы 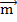 және
және 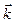 бірлік векторлар. (450)
бірлік векторлар. (450)
95. 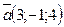 және
және 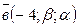 векторлары коллинеар болатындай
векторлары коллинеар болатындай 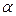 және
және 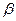 шамаларының мәндерiн тап. (
шамаларының мәндерiн тап. (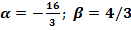 )
)
96. 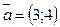 және
және 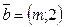 векторлары m-нің қандай мәндерінде перпендикуляр болады? (-8/3)
векторлары m-нің қандай мәндерінде перпендикуляр болады? (-8/3)
97. 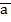 (-2,1,2)
(-2,1,2) 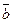 (2, -2, 0) векторлары берілген. 3
(2, -2, 0) векторлары берілген. 3 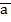 және
және 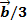 векторларының арасындағы бұрышын табыңыз. (
векторларының арасындағы бұрышын табыңыз. (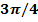 )
)
98. 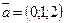 және
және 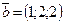 векторлары берілген.
векторлары берілген. 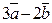 векторларының ұзындығын табыңыз (3)
векторларының ұзындығын табыңыз (3)
99. 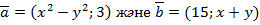 векторлары берілген. Егер
векторлары берілген. Егер 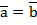 болса, х пен у тап (x=4,y= –1)
болса, х пен у тап (x=4,y= –1)
100. 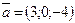 және
және 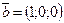 векторлары бойынша салынған параллелограммның ауданын табыңыз (4)
векторлары бойынша салынған параллелограммның ауданын табыңыз (4)
101. 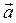 және
және 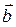 векторларының арасындағы бұрыш 60 0. Егер
векторларының арасындағы бұрыш 60 0. Егер 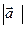 =4,
=4, 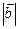 =2 болса,
=2 болса, 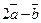 векторының ұзындығы неге тең (2
векторының ұзындығы неге тең (2 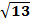 )
)
102. 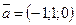 және
және 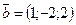 векторларының арасындағы бұрышты табыңыз(3p/4)
векторларының арасындағы бұрышты табыңыз(3p/4)
103. 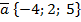 және
және 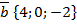 векторларының арасындағы бұрыштың косинусын табыңыз. (-13/15)
векторларының арасындағы бұрыштың косинусын табыңыз. (-13/15)
104. 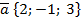 және
және 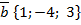 векторларының арасындағы бұрыштың косинусын табыңыз (
векторларының арасындағы бұрыштың косинусын табыңыз (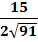 )
)
105. 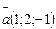 және
және 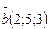 векторларының скалярлық көбейтіндісін т-з (9)
векторларының скалярлық көбейтіндісін т-з (9)
106.  векторларының скалярлық көбейтіндісін т-з (1)
векторларының скалярлық көбейтіндісін т-з (1)
107. 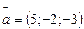 және
және 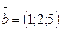 векторларының скалярлық көбейтіндісін т-з (-14)
векторларының скалярлық көбейтіндісін т-з (-14)
108. 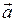 және
және 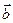 векторларының ұзындықтары
векторларының ұзындықтары 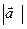 =1,
=1, 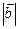 =2,
=2, 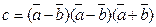 скаляр көбейтіндісі неге тең? (-3)
скаляр көбейтіндісі неге тең? (-3)
109. 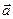 және
және 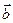 векторларының ұзындықтары
векторларының ұзындықтары 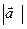 =2,
=2, 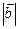 =1,
=1, 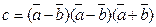 скаляр көбейтіндісі неге тең? (3)
скаляр көбейтіндісі неге тең? (3)
110. 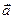 {3;3} және
{3;3} және 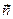 {3;-3} векторларының арасындағы бұрышты табыңыз. (900)
{3;-3} векторларының арасындағы бұрышты табыңыз. (900)
111. 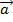 = (5;4;3) және Ох осінің арасындағы бұрышты тап. (
= (5;4;3) және Ох осінің арасындағы бұрышты тап. ( 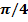 )
)
112. 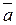 және
және 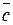 коллениар векторлар. Осы векторлардың белгісіз координаттары
коллениар векторлар. Осы векторлардың белгісіз координаттары 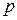 ж/е
ж/е 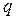 -дің сан мәндерін тап, егер
-дің сан мәндерін тап, егер 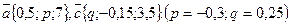
113. 
 және
және 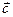 векторлар арасындағы бұрыш
векторлар арасындағы бұрыш 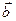 және
және  векторлары арасындағы бұрышқа тең және олар 600-қа тең,
векторлары арасындағы бұрышқа тең және олар 600-қа тең, 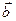 және
және 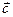 перпендикуляр.
перпендикуляр. 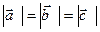 = x болса,
= x болса, 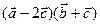 скаляр көбейтіндісін есептеңіз. (-x2)
скаляр көбейтіндісін есептеңіз. (-x2)
114. 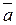 мен
мен 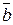 векторларының арасындағы бұрыш 450,
векторларының арасындағы бұрыш 450, 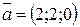 ж/е
ж/е 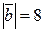 болса, олардың скаляр көбейтіндісін табыңыз. (16)
болса, олардың скаляр көбейтіндісін табыңыз. (16)
115. 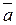 мен
мен 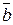 векторларының арасындағы бұрыш 600,
векторларының арасындағы бұрыш 600, 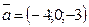 ж/е
ж/е 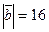 тең болса, онда векторлардың скаляр көбейтіндісін табыңыз. (40)
тең болса, онда векторлардың скаляр көбейтіндісін табыңыз. (40)
116. 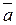 мен
мен 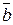 векторларының арасындағы бұрыш 600,
векторларының арасындағы бұрыш 600, 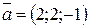 ж/е
ж/е 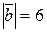 тең болса, онда векторлардың скаляр көбейтіндісін табыңыз. (9)
тең болса, онда векторлардың скаляр көбейтіндісін табыңыз. (9)
117. 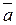 мен
мен 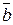 векторларының арасындағы бұрыш 600,
векторларының арасындағы бұрыш 600, 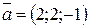 ж/е
ж/е 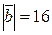 тең болса, онда векторлардың скаляр көбейтіндісін табыңыз. (24)
тең болса, онда векторлардың скаляр көбейтіндісін табыңыз. (24)
118. а1 ═ 2,1; а23 ═ -2,3 болса, арифметикалық прогрессия құрайтын тізбектің айырмасы неге тең болады? d = -0,2
119. а1 ═ 4, d = 2 болатын арифметикалық прогрессияның он мүшесінің қосындысын табыңыз. (180)
120. а1 ═ 4, а18 ═ –13 болса, арифметикалық прогрессия құрайтын тізбектің айырмасы неге тең болады? (d = –1)
121. а1 ═ 7, а16 ═ 67 болса, арифметикалық прогрессия құрайтын тізбектің айырмасы неге тең болады? (d = 4)
122. а1=10, d=4, n=11 болатын арифметикалық прогрессияныңсоңғы мүшесін тап. (50)
123. а4 ═ 10, а7═ 19 болса, арифметикалық прогрессияның он мүшесінің қосындысын табыңыз. (145)
124. а1 ═ 16,а8 ═ 37 болса, арифметикалық прогрессия құрайтын тізбектің айырмасы неге тең болады? (d = 3)
125. a2+a9=20 арифметикалық прогрессияның алғашқы он мүшесінің қосындысын табыңыз. (100)
126. a5=25, a7 = 35 болатын (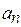 ) арифметикалық прогрессияның бірінші, үшінші және тоғызыншы мүшелері геометриялық прогрессия құрайды. Солардың алғашқы үш мүшенің қосындысын табыңыз. (65)
) арифметикалық прогрессияның бірінші, үшінші және тоғызыншы мүшелері геометриялық прогрессия құрайды. Солардың алғашқы үш мүшенің қосындысын табыңыз. (65)
127. а8 –а6 ═ 6, S10= 155. Осы арифметикалық прогрессияның бірінші мүшесі мен айырымын табыңыз. (a1=2,d=3)
128. (an) арифметикалық прогрессияның бірінші, екінші және бесінші мүшелері геометриялық прогрессияны құрайды. Егер 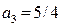 , ал
, ал 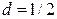 болса, онда геометриялық прогрессияның бесінші мүшесін табыңыз. (8/14)
болса, онда геометриялық прогрессияның бесінші мүшесін табыңыз. (8/14)
129. аn = 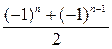 тізбектің алғашқы бес мүшесін табыңыз: (0; 0; 0; 0; 0)
тізбектің алғашқы бес мүшесін табыңыз: (0; 0; 0; 0; 0)
130. аn = 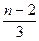 тізбегінің алғашқы үш мүшесін табыңыз: (-
тізбегінің алғашқы үш мүшесін табыңыз: (- 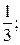 0;
0; 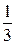 )
)
131. а 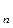 =
= 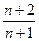 тізбегінің алғашқы бес мүшесін табыңыз: (
тізбегінің алғашқы бес мүшесін табыңыз: (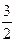 ;
; 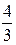 ;
; 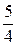 ;
; 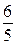 ;
; 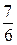 )
)
132. ап = п 2 тізбектің алғашқа бес мүшесін табыңыз: (1; 4; 9; 16; 25)
133. а 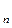 = 2 п +3 тізбегінің алғашқы үш мүшесін табыңыз: (5; 7; 9)
= 2 п +3 тізбегінің алғашқы үш мүшесін табыңыз: (5; 7; 9)
134. an=4n+9 тізбегінің алғашқы он сегіз мүшесінің қосындысын табыңыз:(846)
135. an=5+2n формуласыменберілген тізбек арифметикалық прогрессия, оның алғғашқы он екі мүшесінің қосындысын тап. (216)
136. аn=6n+2 тізбектің алғашқы он алты мүшесінің қосындысын табыңыз: (848)
137. а-ның қандай мәндерінде 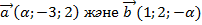 векторларының өзара перпендикуляр болатынын көрсетіңіз? (-6)
векторларының өзара перпендикуляр болатынын көрсетіңіз? (-6)
138. а-ның қандай мәндерінде  векторларының арасындағы бұрыш доғал болады? (
векторларының арасындағы бұрыш доғал болады? ( 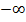 ;–5)
;–5)
139. (a>0) a-ның қандай мәнінде және [0;a] кесіндіде 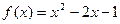 функциясының ең үлкен мәні (-1) – ге тең болады? [ 0:2 ]
функциясының ең үлкен мәні (-1) – ге тең болады? [ 0:2 ]
140. а-ның қандай мәнінде 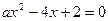 теңдеуінің екі түрі бар? (а≠0)(a<2)
теңдеуінің екі түрі бар? (а≠0)(a<2)
141. а-ның қандай мәндерінде х2+у2=4 және у=а сызықтарының екі ортақ нүктесінің болатынын көрсет. 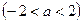
142. а-ның қандай мәндерінде 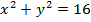 және x=a сызықтарының тек бір ғана ортақ нүктесінің болатынын көрсет. (a=
және x=a сызықтарының тек бір ғана ортақ нүктесінің болатынын көрсет. (a= 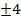 )
)
143. а-ның қандай мәндерінде мына сызықтармен y=2x+2, y=0, x=a шектелген фигураның ауданы 4-ке тең болатынын тап: (1)
144. а-ның қандай мәндерінде мына сызықтармен шектелген фигураның ауданы 9-ға тең:у=х2, у=0, х=а? (3)
145. а-ның қандай мәнінде мына сызықтармен шектелген фигураның ауданы 4-ке тең y = x3, y = 0, x = a (2)
146. а-ның қандай мәнінде 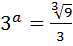 теңдігі орындалады? (-1/3)
теңдігі орындалады? (-1/3)
147. а-ның қандай мәнінде 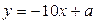 түзуі y =3x2–4x–2 функциясының графигіне жанама болады? (а=-5)
түзуі y =3x2–4x–2 функциясының графигіне жанама болады? (а=-5)
148. а-ның қандай мәнінде 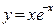 функциясы
функциясы 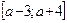 аралығында өседі (-
аралығында өседі (- 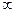 ;-3 ]
;-3 ]
149. а-ның қандай мәнінде 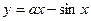 функциясы барлық сан өсінде өспелі. (a>1)
функциясы барлық сан өсінде өспелі. (a>1)
150. а-ның қандай мәнінде 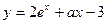 функциясының кризистік нүктелері болмайтынын табыңыз [ 0;+
функциясының кризистік нүктелері болмайтынын табыңыз [ 0;+ 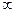 )
)
151. а-ның қандай мәнінде 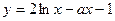 функциясының кризистік нүктелері болмайтынын табыңыз (-
функциясының кризистік нүктелері болмайтынын табыңыз (- 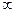 ;0 ]
;0 ]
152. а-ның қандай мәнінде 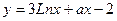 функциясының кризистік нүктелері болмайтынын табыңыз [ 0;+
функциясының кризистік нүктелері болмайтынын табыңыз [ 0;+ 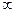 )
)
153. а-ның қандай мәнiнде теңдік орындалады: 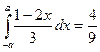 (а=2/3)
(а=2/3)
154. а-ның қандай мәндерiнде 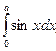
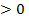 теңсiздiгi орындалады? (
теңсiздiгi орындалады? (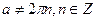 )
)
155. а-ның қандай мәндерінде 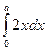 <3 теңсіздігі орындалады?
<3 теңсіздігі орындалады? 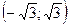
156. 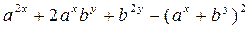 өрнегін ықшамдаңыз.(0)
өрнегін ықшамдаңыз.(0)
157. 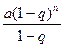 өрнегінің a=8, q=-1/2, n=4 болғандағы сан мәнін табыңыз.(27)
өрнегінің a=8, q=-1/2, n=4 болғандағы сан мәнін табыңыз.(27)
158. 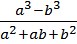 өрнегінің a=5/4, b=1/4 болғандағы сан мәнін табыңыз.(1)
өрнегінің a=5/4, b=1/4 болғандағы сан мәнін табыңыз.(1)
159. 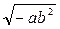 өрнегнің мағынасы болу үшін қандай шарт жеткілікті? (a<0)
өрнегнің мағынасы болу үшін қандай шарт жеткілікті? (a<0)
160. а параметрінің қандай мәнінде интеграл 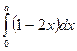 максимум мәнін қабылдайды? а=
максимум мәнін қабылдайды? а= 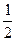
161. а параметрінің қандай мәнінде интеграл 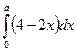 3-тен артпайды?
3-тен артпайды?
(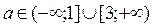 )
)
162. а параметірінің қандай мәнінде 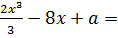 0 қисығы абцисс өсімен жанасады (a=32/3,a=-32/3)
0 қисығы абцисс өсімен жанасады (a=32/3,a=-32/3)
163. а параметірінің қандай мәнінде 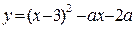 функциясы жұп болып табылады? (-6)
функциясы жұп болып табылады? (-6)
164. а саны 5-ке бөлінеді. b саны 5-ке бөлгенде 1 қалдық қалады. Ал с санын 5-ке бөлгенде 2 қалдық қалады. a+b+c қосындысын 5-ке бөлгенде қандай қалдық қалады? (3)
165. а санына қарама-қарсы сан мен 3-тің қосындысын әріпті өрнек түрінде жаз. (а+3)
166. а түзуі β жазықтығымен қиылысады, ал β жазықтығы γ жазықтығына паралелль. а түзуі мен γ жазықтығының өзара орналасуы (қиылысады)
167. а түзуі β жазықтығына перпендикуляр, ал β жазықтығы с түзуіне параллель. а және с түзулерінің өзара орналасуы (перпендикуляр)
168. а түзуі b түзуіне параллель, ал b түзуі γ жазықтығымен қиылысады, а түзуі мен γ жазықтығының өзара орналасуы (қиылысады)
169. а түзуі b түзуіне перпендикуляр, ал b түзуі γ жазықтығына перпендикуляр. а түзуі мен γ жазықтығының өзара орналасуы (а түзуі мен γ жазықтығына параллель немесе γ жазықтығында жатады)
170. а түзуі b түзуіне перпендикуляр, ал b түзуі с түзуіне параллель. а және с түзулерінің өзара орналасуы. (перпендикуляр)
171. 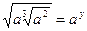 , y-ті табыңыз(5/6)
, y-ті табыңыз(5/6)
172. α жазықтығы ABC үшбұрышының АВ және ВС қабырғаларын сәйкесінше Д және Е нүктелерде кияды. AC║a. ВД:АД=3:4 және ДЕ=10см болса, АС-ны таб. (23  см)
см)
173. α жазыктығы b түзуіне перпендикуляр, ал b түзуі γ жазықтығына перпендику-ляр. а және γ жазыктықтарының өзара орналасуы. (параллель н/е беттеседі)
174. α жазықтығы b түзуіне перпендикуляр, ал b түзуі с түзуіне параллель. а
175. жазықтығы мен с түзуінің өзара орналасуы. (перпендикуляр)
176. α жазықтығыb түзуіне параллель, ал b түзуі γ жазықтығына перпендикуляр. a және γ жазықтықтарының өзара орналасуы. (перпендикуляр)
177. α жазықтығы 𝛃 жазықтығына параллель, ал 𝛃 жазықтығы γ жазықтығына перпендикуляр. a және γ жазыктыктарының өзара орналасуы. (перпендикуляр)
178. α жазықтығы мен α-дан тыс М нүктесі берілген. α жазықтығына параллель М нүктесі арқылы өтетін канша жазықтық жүргізуге болады? (жалғыз)
179. α жазықтығы мен α-дан тыс М нүктесі берілген. α жазыктығына парал-лель М нүктесі арқылы өтетін қанша түзу жүргізуге болады? (шексіз көп)
180. α жазықтығы мен М нүктесі берілген. α жазықтығына перпендикуляр М нүктесі арқылы өтетін қанша жазықтық жүргізуге болады? (шексіз көп)
181. α жазықтық, ал О жазықтықтан тыс жатқан нүкте. О нүктесінен α жазықтығын А және В нүктелерінде киятын екі түзу жүргізілген OA және ОВ кесінділерінің орталары сәйкесінше С және D. CD=7 деп алып, АВ кесіңдісі-нің ұзындығы? (14)
182. α және 𝛃 жазықтықтары с түзуі бойымен 60° бұрыш жасап қиылысқан. A нүктесі α жазықтығында жатыр және β жазықтығынан 10 см қашықтықта орналасқан. А нүктесінен с түзуіне дейінгі арақашықтық неге тең? (20/ 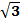 )
)
183. α және 𝛃 жазықтықтары перпендикуляр. α жазықтығы а түзуіне, β жазықтығы b түзуіне перпендикуляр. a және 𝛃 жазықтық-ң өзара орналасуы. (перпендикуляр)
184. α және 𝛃 жазықтықтары перпендикуляр. а түзуі α жазықтығы, β жазықтығына перпендикуляр. a және b түзулерінің өзара орналасуы. (перпендикуляр)
185. α және 𝛃 жазықтықтары с түзуі бойымен 30° бұрыш жасап қиылысқан. A нүктесі α жазықтығында жатыр және β жазықтығынан 10 см қашықтықта орналасқан. А нүктесінен с түзуіне дейінгі арақашықтық неге тең? (20см)
186. α және 𝛃 жарты жазықтығымен құралған екі жақты бұрыш 90°-қа тең. A нүктесі екі жарты бұрышының жақтарынан 8см мен 6см қашықтықта орналасқан. А нүктесінен екі жақты бұрыштың қырына дейінгі қашықтықты табыңыз. (10)
187. 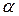 қандай мәнінде
қандай мәнінде 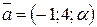 және
және 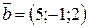 векторлардың арасындағы бұрыш доғал болады. (–∞;4,5)
векторлардың арасындағы бұрыш доғал болады. (–∞;4,5)
188. а-ның қандай мәнiнде 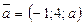 және
және 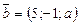 векторының арасындағы бұрыш сүйiр болады?
векторының арасындағы бұрыш сүйiр болады? 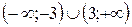
189. 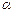 - ның қандай мәнiнде
- ның қандай мәнiнде 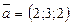 және
және 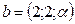 векторларының арасындағы бұрыш сүйір болады? (–5;+∞)
векторларының арасындағы бұрыш сүйір болады? (–5;+∞)
190. 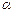 - ның қандай мәнiнде
- ның қандай мәнiнде 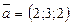 және
және 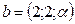 векторларының арасындағы бұрыш доғал болады?
векторларының арасындағы бұрыш доғал болады? 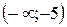
191. а-ның қандай мәнiнде 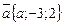 және
және 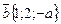 векторларының өзара перпендикуляр болатынын көрсетiңiз: (-6)
векторларының өзара перпендикуляр болатынын көрсетiңiз: (-6)
192. 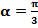 мәніндегі,
мәніндегі, 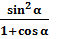 өрнегін есептеңіз.(1/2)
өрнегін есептеңіз.(1/2)
193. 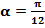 мәніндегі,
мәніндегі, 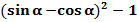 өрнегін есептеңіз.(–1/2)
өрнегін есептеңіз.(–1/2)
194. Абсцисса осімен 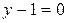 түзуімен
түзуімен 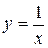 гиперболамен және [0;e] кесіндісімен шектелген фигураның ауданын табыңыз.(2)
гиперболамен және [0;e] кесіндісімен шектелген фигураның ауданын табыңыз.(2)
195. Абсцисса осіне параллель болатын 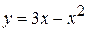 функциясының графигіне жүргізілген жанаманың теңдеуін табыңыз. (у=9/4)
функциясының графигіне жүргізілген жанаманың теңдеуін табыңыз. (у=9/4)
196. Абсциссасы 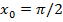 болатын нүктесінде
болатын нүктесінде 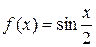 функциясының графигіне жүргізілген жанаманың бұрыштық коэффициентін табыңыз.(
функциясының графигіне жүргізілген жанаманың бұрыштық коэффициентін табыңыз.(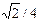 )
)
197. Абсциссасы 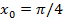 болатын нүктеде
болатын нүктеде 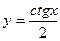 қисығына жүргізілген жанама Ох осіне қандай бұрышпен көлбеген? (
қисығына жүргізілген жанама Ох осіне қандай бұрышпен көлбеген? (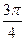 )
)
198. Абциссасы 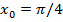 болатын нүктеде
болатын нүктеде 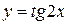 қисығына жүргізілген жанаманың Ох осімен жасайтын бұрышы қандай болады?
қисығына жүргізілген жанаманың Ох осімен жасайтын бұрышы қандай болады? 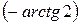
199. Абсциссасы х0 ═ – 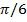 болатын нүктеде y = cos 2x қисығына жүргізілген жанама Ох осіне қандай бұрышпен көлбеген. (
болатын нүктеде y = cos 2x қисығына жүргізілген жанама Ох осіне қандай бұрышпен көлбеген. ( 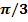 )
)
200. Абциссасы 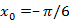
|
|
|
|
|
Дата добавления: 2017-02-24; Мы поможем в написании ваших работ!; просмотров: 2136 | Нарушение авторских прав
Лучшие изречения:






