А1. Елементи векторної алгебри
В геометрії вектором (в вузькому сенсі) зветься будь-який направлений відрізок, який має початок та кінець. Кінець вектора позначається стрілкою.
Модулем вектора зветься його довжина (звичайні позначки 
чи 
).
Два ненульових вектора вважаються рівними, коли вони мають однакову довжину (модуль) та однаковий напрям (повністю співпадають при паралельному переносі - дивись рис. 1, на якому 
, 
, 
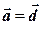). Всі нульові вектори вважаються рівними. У всіх інших випадках вектори не рівні. Кутом між векторами є кут між їх напрямами.
Вираз „ проекція векторана вісь ” має два тлумачення:
а) Геометрична проекція вектора 
на вісь– вектор, початок якого є проекція початку вектора на вісь, а кінець – проекція кінця вектора 
на вісь (наприклад, 
та 
на рис. 2). Модуль вектора може бути визначено за його проекціями в прямокутній системі координат
= 
.
б) Алгебраїчна проекція вектора на вісь– число, яке дорівнює різниці координат кінця і початку вектора (наприклад, для вектора 
, рис. 2, маємо: 
> 0, 
< 0).
Складання векторів (операція однозначна) – сумою векторів і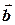 
зветься вектор 
, який побудовано за будь-яким з наступних правил:
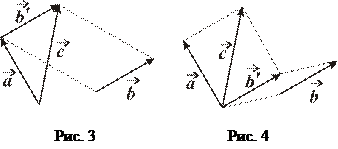
- Правило трикутника – вектор 
переноситься паралельно самому собі таким чином, щоб його початок був розташований в кінці вектора 
. Сумою векторів буде вектор 
, який проведено з початку вектора в кінець вектора 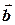(дивись рис. 3).
- Правило паралелограма - вектор 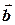переноситься паралельно самому себе таким чином, щоб його початок був розташований в початку вектора . Сумою векторів буде вектор 
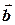- діагональ паралелограма, яка проведена з початку вектора у протилежний кут паралелограма побудованого на сторонах і (дивись рис. 4).
Якщо відомі проекції векторів і 
(
, 
, 
) та (
, 
, 
), то
= + , 
= + , 
= + .
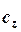Добуток вектора і скаляра
Добутком вектора на скалярну величину 
є вектор 
, який в 
разів довший, ніж вектор . Цей вектор спрямований у той же бік, що і вектор , якщо додатна і в протилежний, якщо від’ємна.
Скалярний добуток векторів
Скалярний добуток векторів ( і ) – це число 
, яке визначається за наступними правилами: = 
= 
, де 
– кут між векторами і . Скалярний добуток дорівнює нулю, якщо модуль одного чи обох векторів дорівнює нулю, або коли вектори взаємно перпендикулярні.
Якщо відомі проекції векторів (, , ) та (, , ),то в декартовій системі координат
= · + · + · .
Зауважимо, що · = · .
Векторний добуток векторів
Векторний добуток векторів і – це вектор 
, модуль якого визначається як 
, де – кут між векторами і . Результуючий вектор розташовано перпендикулярно до векторів і , а його напрям визначається за правилом правого свердлика: якщо обертати перший вектор так, щоб найкоротшим поворотом сумістити його з другим, то поступальний рух свердлика вкаже напрям добутку векторів. Векторний добуток дорівнює нулю, якщо модуль одного чи обох векторів дорівнює нулю, чи вектори паралельні.
Якщо відомі проекції векторів (, , ) і (, , ) в декартовій системі координат, то
.
Тут 
, 
, 
- орти декартової системи координат. Тоді:
,
,
.
Зауважимо, що 
.
