Исследование поведения автоматов в стационарной случайной среде. Целесообразные автоматы.
Понятие о конечном автомате. Целесообразные автоматы. Асимптотически-оптимальная последовательность автоматов.
Конечный автомат – объект, имеющий конечное число внутренних состояний (состояний памяти) 
(
), конечное число входных сигналов 
(
) и конечное число выходных сигналов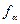 
(
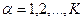). Предполагается, что автоматы функционируют в дискретном времени, т.е. время принимает целочисленные значения.
Автомат зададим каноническими уравнениями:
 ,
| (1) |
 ,
| (2) |
где уравнение (1) определяет смену внутренних состояний под воздействием входной величины, а уравнение (2) – зависимость выходного сигнала от внутреннего состояния автомата.
Функция перехода автомата может быть задана либо системой матриц 
, которые определяют смену состояний автомата (
) (
) под воздействием сигнала (), либо ориентированными графами состояний.
Автоматы могут быть детерминированными или стохастическими. Для детерминированных автоматов матрицы являются простыми, т.е. каждая их строка содержит только один элемент равный единице, а остальные элементы строки равны нулю. Для стохастических автоматов матрицы - стохастические (
, 
). Каждый элемент 
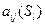матрицы определяет вероятность перехода автомата из состояния в состояние 
под воздействием входного сигнала .
Рассмотрим поведение автомата во внешней среде С. Это означает, что выходные сигналы автомата 
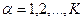() являются входными сигналами для некоторого устройства C, которое реагирует на них сигналами являющимися входными для автомата. Выходные сигналы 
называют действиями, а входные сигналы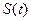 
- реакцией среды С. Будем считать, что реакции среды С, воспринимаемые автоматом, делятся на два класса: класс благоприятных реакций 
= +1 (выигрыш, поощрение, вознаграждение) и класс неблагоприятных реакций = -1 (проигрыш, штраф).
Рассмотрим простейшую задачу о поведении автомата в стационарной случайной среде С (
), где 
постоянны и не зависят от времени. Автомат A функционирует в случайной среде С (), если действие автомата 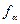(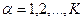), произведенное автоматом в момент времени t, влечёт за собой в момент времени t +1 значение 
= -1 (штраф) с вероятностью 
и значение = +1 (поощрение) с вероятностью 
.
Поведение системы “автомат – случайная стационарная среда” описывается дискретной цепью Маркова. В том случае, когда конструкция автомата (набор матриц 
и 
) такова, что цепь Маркова эргодична, существуют финальные вероятности состояний, не зависящие от начального состояния.
Обозначим через 
финальную вероятность состояния 
автомата в среде C и через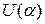 
(
) финальную вероятность действия . Математическое ожидание выигрыша 
автомата А в среде С определяется формулой
.
Очевидно, что
.
Если автомат выбирает свои действия независимо от реакций среды и равновероятно, то математическое ожидание его выигрыша
.
Говорят, что автомат А обладает целесообразным поведением в стационарной случайной среде С, если
.
Задача построения автомата, обладающего целесообразным поведением в данной среде С, тривиальна, т.к. её решением является автомат с одним внутренним состоянием, в котором он выполняет то действие, за которое в данной среде полается минимальный штраф. Такой автомат обладает “априорной целесообразностью”, т.е. целесообразность его поведения основывается на априорном знании параметров случайной среды.
В дальнейшем нас будут интересовать автоматы, которые “априорной целесообразностью” не обладают, т.е. симметрические автоматы случайных сред, получаемых из сред С (), всеми возможными перестановками параметров . В этом случае, функция является симметрической функцией параметров .
Нас будут интересовать конструкции автоматов, для которых приближается к 
. Введём следующее определение:
Последовательность автоматов 
называется асимптотически - оптимальной, если
.
Автомат, принадлежащий асимптотически-оптимальной последовательности, при достаточной величине номера m производит почти всегда то действие, при котором вероятность выигрыша максимальна. В качестве номера автомата в последовательности мы будем использовать число состояний памяти, называя его емкостью (глубиной) памяти.
