III Силовой анализ рычажного механизма
Целью силового анализа является получение значений сил и реакции в кинематических парах для последующего расчета на прочность и определения потерь мощности на трение.
Согласно заданию, силовой анализ производим для второго положения механизма.
Определение угловой скорости и углового ускорения
Кривошипного вала с учетом маховика
Определим величину угла сдвига амплитуды угловой координаты n-й гармоники с учетом маховика.
 (3.1)
(3.1)
Для n=1 получим:
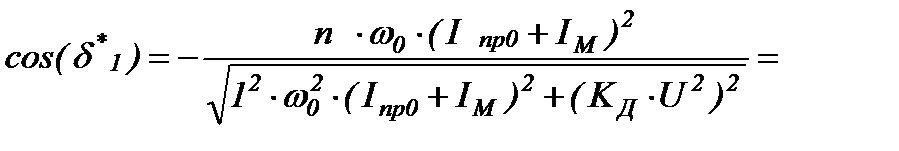

 (3.2)
(3.2)
Для n=1 получим:

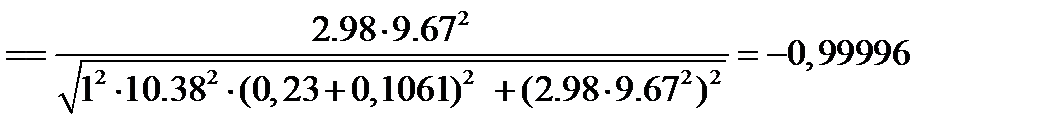
Аналогично определяем  и
и  результаты представлены в виде таблицы 3.1
результаты представлены в виде таблицы 3.1
Таблица 3.1 Численные значения угла сдвига амплитуды угловой координаты
cos 
| 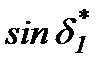
| 
| 
| 
| 
|
| -0.00911 | -0,99996 | -0,01822 | -0,99983 | -0,02732 | -0,99963 |
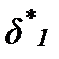 =269,4781° =269,4781°
|  =268,9563° =268,9563°
|  =268.4347° =268.4347°
|
Определим амплитудные значения динамического отклонения угловой координаты с учетом маховика
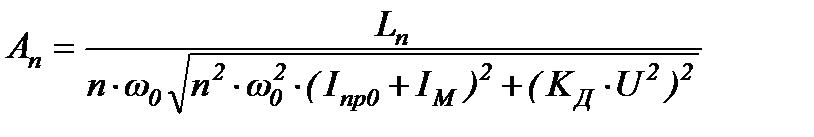 (3.3)
(3.3)
Для n=1 получим:


Таблица 3.2 Численные значения амплитудного
значения динамического отклонения
| А1,м | А2,м | А3,м |
| 0,06412759 | 0,0016414 | 0,00343675 |
Угловая скорость кривошипного вала с учетом маховика определяются по формулам:
 (3.4)
(3.4)
Для пятого положения находим:

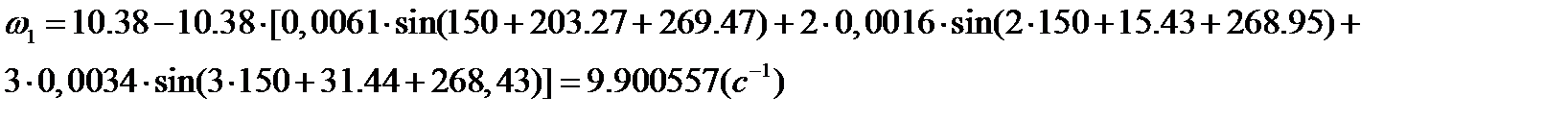
Угловое ускорение кривошипного вала с учетом маховика определяются по формулам:
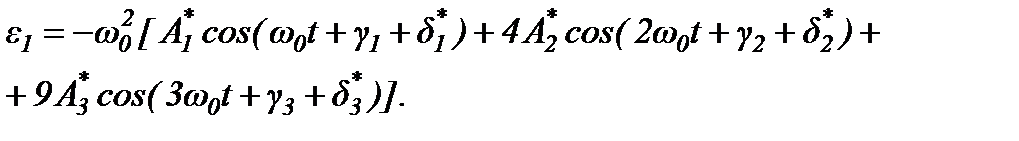 (3.5)
(3.5)
Для пятого положения находим:

Построение планов ускорений
Определим ускорение точки А кривошипа 1 из уравнения:
 ; (3.6)
; (3.6)
где:  –вектор ускорения точки 0;
–вектор ускорения точки 0;
 – вектор ускорении точки А относительно О, направлен параллельно кривошипу 1 к центру его вращения;
– вектор ускорении точки А относительно О, направлен параллельно кривошипу 1 к центру его вращения;
 – вектор ускорении точки А относительно О, направлен перпендикулярно кривошипу.
– вектор ускорении точки А относительно О, направлен перпендикулярно кривошипу.
Определим численное значение вектора ускорения  точки А:
точки А:
 (3.7)
(3.7)
Определим численное значение вектора ускорения  точки А
точки А

Построение планов ускорений начинаем с выбора масштаба плана для 5-го положения механизма
Для этого определим величину отрезка изображающего вектор  на плане. Имеем:
на плане. Имеем:
 (3.8)
(3.8)
где:  масштаб плана ускорений.
масштаб плана ускорений.
Из произвольно выбранной на плане точки  принятой за полюс, откладываем в масштабе
принятой за полюс, откладываем в масштабе 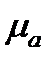 вектор
вектор  .
.
Составим векторное уравнение для структурной группы 2-3 механизма.
 ; (3.9)
; (3.9)
где:  – вектор нормального ускорения точки B относительно А, направлен параллельно шатуну 2 в сторону точки А;
– вектор нормального ускорения точки B относительно А, направлен параллельно шатуну 2 в сторону точки А;
 – вектор тангенциального ускорении точки B относительно А, направлен перпендикулярно шатуну 2.
– вектор тангенциального ускорении точки B относительно А, направлен перпендикулярно шатуну 2.
Определим численное значение вектора нормального ускорения  .
.
 (3.10)
(3.10)
где: 
Решим векторное уравнение (3.9) графически. Для этого из конца вектора  в масштабе
в масштабе 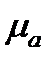 откладываем вектор
откладываем вектор  параллельно шатуну АB, в направлении точки А. Через полюс
параллельно шатуну АB, в направлении точки А. Через полюс  плана проводим направляющую ОB ускорения
плана проводим направляющую ОB ускорения  . Чрез конец вектора
. Чрез конец вектора  проводим направляющую вектора
проводим направляющую вектора  , перпендикулярно АB, до пересечения с направляющей ОB. Из полученного плана находим:
, перпендикулярно АB, до пересечения с направляющей ОB. Из полученного плана находим:

(3.11)
где: n2в – отрезок изображающий вектор  на плане.
на плане.
Составим векторное ускорение для структурной группы 4-5 механизма.
 ; (3.12)
; (3.12)
Определим численное значение вектора нормального ускорения  .
.
 (3.13)
(3.13)
где: 
Решим векторное уравнение (3.12) графически. Для этого из конца вектора 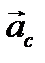 в масштабе
в масштабе 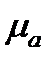 откладываем вектор
откладываем вектор  параллельно шатуну АC в направлении точки А. Через полюс
параллельно шатуну АC в направлении точки А. Через полюс  плана проводим направляющую ОС ускорения
плана проводим направляющую ОС ускорения  . Чрез конец вектора
. Чрез конец вектора  проводим направляющую вектора
проводим направляющую вектора  , перпендикулярно АС, до пересечения с направляющей ОС. Из полученного плана находим:
, перпендикулярно АС, до пересечения с направляющей ОС. Из полученного плана находим:
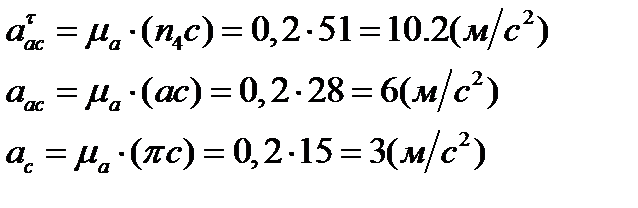
(3.14)
где: n4с – отрезок изображающий вектор  на плане;
на плане;
 - отрезок изображающий вектор
- отрезок изображающий вектор  на плане.
на плане.
По теореме подобия определим положение точек s2 и s4 на плане ускорении. Имеем:
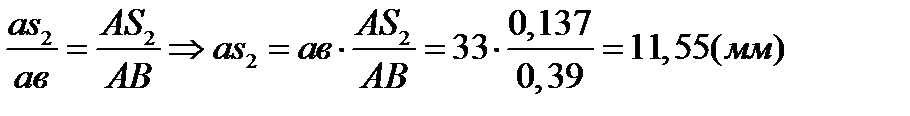 (3.15)
(3.15)
и
 (3.16)
(3.16)
Соединив полученную точку с полюсом  плана, получим:
плана, получим:
 (3.17)
(3.17)
 (3.18)
(3.18)
Определим угловое ускорение звена 2.
 (3.19)
(3.19)
 (3.20)
(3.20)
где:  – тангенциальное ускорение точки В вокруг А.
– тангенциальное ускорение точки В вокруг А.
Результаты расчета ускорений представим в виде таблицы 3.3.
Таблица 3.3 Ускорения характерных точек механизма в пятом положении
| Положение механизма | 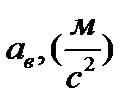
| 
| 
| 
| 
| 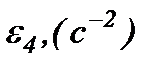
|
| 13,2 | 11,6 | 8,4 | 15,4 | 26,2 |
Построение планов сил
Цель силового расчета – определение реакций в кинематических парах под действием внешних сил и сил инерции, а также качественная оценка спроектированного механизма.
Силовой анализ выполняем графоаналитическим методом на примере 10-го положения механизма.
В заданном положении на звенья механизма действуют:
сила полезного сопротивления Рпс.3= 0 Н;
сила полезного сопротивления Рпс.5= 550 Н;
силы тяжести звеньев
Gi = mi·g (3.21)
Для кривошипа 1 имеем:
G1 = (m1+mм)·g = (1,14+2,34) ·9,81=34,1(Н)
силы и моменты сил инерции для десятого положения
Силы инерции определяем по формуле
Ри= –mi·asi (3.22)
Знак минус указывает на то, что сила инерции направлена в строну противоположную ускорению. Для шатуна находим:
Ри2=m2·aS2= -4,64·11,6= –53,8 (H);
Момент сил инерции определяется по формуле
Ми = – IS·ε (3.23)
Знак минус указывает на то, что момент инерции направлен в строну противоположную ускорению
Mи2= Is2·ε2=-0,12·15,4=-1,8 (H·м);
Таблица 3.4 Силы тяжести, инерции и моменты сил инерции
| П.К. | G1,(Н) | G2,(Н) | G3,(Н) | G4,(Н) | G5,(Н) | Ри2,(Н) | Ри3,(Н) | Ри4,(Н) | Ри5,(Н) | Mи2,(н·м) | Mи4,(н·м) |
| 34,1 | 46,4 | 58,4 | 46,4 | 25,6 | -53,8 | -49,1 | -53,8 | -29,7 | -1,8 | -0,1 |
Расчленяем механизм на структурные группы, вычерчиваем их отдельно в масштабе
μl =0,002(м/мм) прикладываем к соответствующим точкам силы и реакции расчлененных кинематических пар.
Силовой анализ начинаем со структурной группы Ассура 4-5.
Воздействие звена 5 и стойки 0 на звенья отсоединенной группы 4-5 заменяем силами реакций. В соответствии с принципом Даламбера условие равновесия структурной группы 4-5 имеет вид:
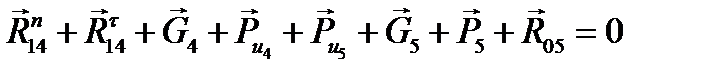 (3.24)
(3.24)
Это уравнение имеет три неизвестных:  Реакцию
Реакцию  определяем из уравнения моментов сил, действующих на звено 4, составленного относительно шарнира С:
определяем из уравнения моментов сил, действующих на звено 4, составленного относительно шарнира С:
 (3.25)
(3.25)
где:  – направлен перпендикулярно АС;
– направлен перпендикулярно АС;
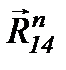 – направлен параллельно АС;
– направлен параллельно АС;
 – направлен перпендикулярно ОС.
– направлен перпендикулярно ОС.
Откуда находим:
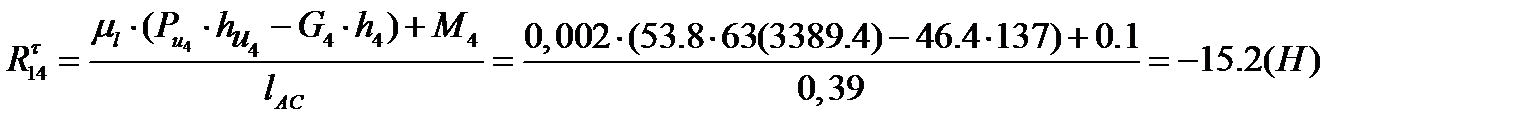 (3.26)
(3.26)
Величину векторов 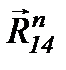 и
и  определяем построением плана сил в масштабе μР=20 Н/мм.
определяем построением плана сил в масштабе μР=20 Н/мм.
Решим уравнение (3.24) графически: Откладываем в принятом масштабе  затем из его конца откладываем вектор
затем из его конца откладываем вектор  из его конца откладываем
из его конца откладываем  и так последовательно, согласно уравнения (3.24), соединяем векторы:
и так последовательно, согласно уравнения (3.24), соединяем векторы:  и
и  . Через конец последнего вектора
. Через конец последнего вектора  , проводим направляющую для вектора
, проводим направляющую для вектора  , а через начало вектора
, а через начало вектора  проводим перпендикулярно ОС линию действия вектора нормальной реакции
проводим перпендикулярно ОС линию действия вектора нормальной реакции 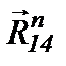 до пересечения с линей действия вектора
до пересечения с линей действия вектора  . Соединяем векторы
. Соединяем векторы 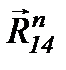 и
и  так, чтобы силовой многоугольник был замкнутым.
так, чтобы силовой многоугольник был замкнутым.
Получим:

 (3.27)
(3.27)

Давление в промежуточном шарнире Д определяем составив уравнение равновесия звена 4
 (3.28)
(3.28)
Модуль реакций  определяется из плана сил:
определяется из плана сил:
 =
=  (3.29)
(3.29)
Группа Ассура 2-3
Уравнение равновесия группы имеет вид:
 (3.30)
(3.30)
Для определения величины реакции  составляем уравнение моментов относительно шарнира В из которого находим:
составляем уравнение моментов относительно шарнира В из которого находим:
 (3.31)
(3.31)
Решим уравнение (3.30) графически: Откладываем в масштабе  :
: 
затем из его конца откладываем  из его конца откладываем
из его конца откладываем  и так последовательно, согласно уравнения (3.30), соединяем векторы:
и так последовательно, согласно уравнения (3.30), соединяем векторы:  и
и  . Через конец последнего вектора
. Через конец последнего вектора  , проводим направляющуюго для вектора
, проводим направляющуюго для вектора  , а черз начало вектора
, а черз начало вектора  проводим перпендикулярно ОВ линию действия вектора нормальной реакции
проводим перпендикулярно ОВ линию действия вектора нормальной реакции  до пересечения с линей действиия вектора
до пересечения с линей действиия вектора  . Соединяем векторы
. Соединяем векторы  и
и  так, чтобы силовой многоугольник был замкнутым. Получим:
так, чтобы силовой многоугольник был замкнутым. Получим:

 (3.32)
(3.32)

Рассмотрим равновесие звена –2–
 (3.33)
(3.33)
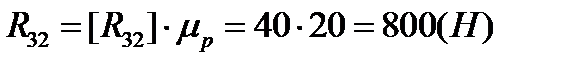 (3.34)
(3.34)
Определив реакцию  переходим к силовому расчету входного звена. В шарнире А прикладываем реакции
переходим к силовому расчету входного звена. В шарнире А прикладываем реакции 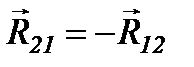 и
и  . Воздействие стойки 0 в шарнире О заменяем реакцией
. Воздействие стойки 0 в шарнире О заменяем реакцией  . Составляем уравнение равновесия звена 1,
. Составляем уравнение равновесия звена 1,  :
:
 (3.35)
(3.35)
В уравнении уравновешивающую силу находим из уравнения моментов относительно точки О. Имеем:

где: Ми.м.=Iм·ε1=-0,0017·(-1,5)=0,0025(н·м)
Решая уравнение (3.34) графически, из построенного плана сил находим:

Уравновешивающий момент будет равен:
МУР = РУР × lОА=600·0,095=57 (н·м) (3.36)
Результаты расчета силового анализа сводим в таблицу 3.5.
Таблица 3.5 Результаты силового анализа
механизма
| Наименование параметра | Численное значение |
Сила  ,Н ,Н
| |
Сила 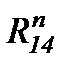 ,Н ,Н
| |
Сила  ,Н ,Н
| -15,2 |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| 5,04 |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| |
Сила  ,Н ,Н
| 1054,7 |
Момент  ,Н·м ,Н·м
| |
Сила  ,Н ,Н
|
Определение потерь мощности на трение
Потери мощности на трение в поступательных кинематических парах:
 (3.37)
(3.37)
где:  - приведенный коэффициент трения для цилиндрических ползунов;
- приведенный коэффициент трения для цилиндрических ползунов;
 - сила давление в паре, образованной звеньями i и к, Н;
- сила давление в паре, образованной звеньями i и к, Н;
 - относительная скорость звеньев кинематической пары, м/с.
- относительная скорость звеньев кинематической пары, м/с.
 =
= 
Потери мощности на трение во вращательных кинематических парах:
 (3.38)
(3.38)
где:  - приведенный коэффициент трения для новых вращательных кинематических пар;
- приведенный коэффициент трения для новых вращательных кинематических пар;
 - сила давление в паре, образованной звеньями i и к, Н;
- сила давление в паре, образованной звеньями i и к, Н;
 и
и  - угловые скорости звеньев кинематической пары, с-1.
- угловые скорости звеньев кинематической пары, с-1.
 - диаметр цапфы, м.
- диаметр цапфы, м.
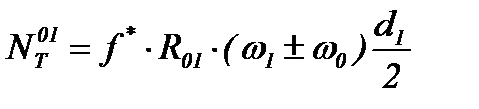
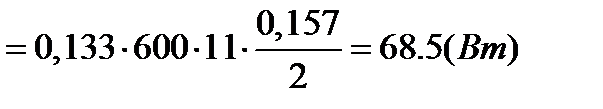
Результаты расчета потерь на трение сводим в таблицу 3.8.
Таблица 3.8 Потери на трение в кинематических парах

| 
| 
| 
| 
| 
| 
|
| 64.1 | 25.6 | 68.5 | 102.7 | 68.5 | 91.3 | 125.5 |
Абсолютные потери мощности на трение равны:
 (3.39)
(3.39)
Коэффициент потерь составляет:
 .=
.=  (3.40)
(3.40)
Мгновенное значение КПД механизма будет равно:
 1-0,47=0,53 (3.41)
1-0,47=0,53 (3.41)
Литература
1. Артоболевский И.И. Теория механизмов и машин/ И.И. Артоболевский. М. Наука 1988.
2.. Гордеенко В.К., Саскевич М.К., Гордеенко О.В. Теория механизмов и машин. -М. Часть 1 Горки, 2004 г.
3. Гордеенко В.К., Саскевич М.К., Гордеенко О.В. Теория механизмов и машин. -М. Часть 2: Горки, 2006 г.
4. Гордеенко В.К., Саскевич М.К., Гордеенко О.В. Теория механизмов и машин. -М. Часть 3 «Силовой анализ механизмов»: Горки, 2007.3600






