Рассмотрим следующую задачу. Пусть n изделий (деталей) должны проходить последователь-ную обработку на двух станках M 1 и M 2 (в указанном порядке), причем станок в каждый момент вре-мени может обрабатывать одну деталь. Продолжительность обработки детали Pj станком Mi предполагается известной; обозначим её через τij. Требуется минимизировать общее время обработки всех деталей на обоих станках.
Конечно, названия «деталь» и «станок» здесь условны; вместо них речь может идти о любых объектах, с которыми надо осуществить две последовательные операции. Например, такими объекта-ми могут быть пациенты, которые должны пройти две медицинских процедуры, приблизительная продолжительность которых известна (так, при курортно-санаторном лечении каждому пациенту ука-зывается продолжительность нахождения в радоновой или другой специальной ванне – обычно от 5 до 20 минут).
Ясно, что 1-й станок может начать обрабатывать следующую деталь сразу же, как только закон-чит обработку предыдущей. Поэтому простоев у него не будет. Иначе обстоит дело со 2-м станком. Он может начать обработку очередной детали только в том случае, когда
а) эта деталь уже обработана на 1-м станке;
б) предыдущая деталь уже обработана на 2-м станке.
Поэтому у 2-го станка возможны простои. Легко понять, что общее время обработки всех дета-лей на 1-м станке не зависит от порядка, в котором эти детали обрабатываются (оно равно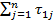 
). Время же обработки всех деталей на 2-м станке (считая от момента, когда начал работу 1-й станок), равно сумме времени, в течение которого 2-й станок работал (оно равно 
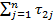и не зависит от по-рядка), и времени простоя. Поэтому исходная задача сводится к минимизации времени простоя.
То, что время простоя (а вместе с ним, следовательно, и общее время обработки вcех деталей) зависит от порядка, в котором они поступают, можно продемонстрировать на примере.
Пример 1. Пусть числа τij (i = 1, 2; j = 1, …, n) приведены в таблице 1. Временнáя диаграмма об-работки деталей в порядке 1, 2, 3, 4, 5, 6 представлена на рис.1а; в порядке 5, 2, 4, 3, 6, 1- на рис 1b. Общий выигрыш 2-го варианта по сравнению с 1-м составляет 3 единицы времени.
Таблица 1
| i | ||||||
| ||||||
|
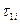
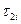
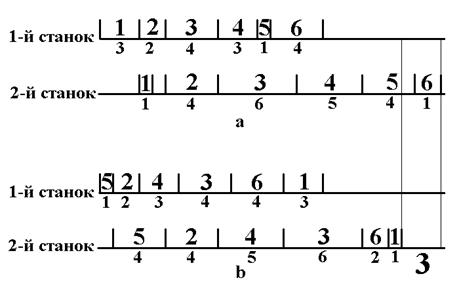
Рис.1. Временные диаграммы при различном упорядочении. Выигрыш составляет три единицы, или 11,5%.
Общее число вариантов (т.е. мощность допустимого множества A) в данном случае совпадает с общим числом всех возможных порядков поступления деталей на обработку, которое, очевидно, рав-но n!. Рассматриваемая здесь задача и состоит в выборе такого варианта, при котором общее время обработки всех деталей (или, что эквивалентно, общее время простоя 2-го станка) минимально. Эта задача получила название задачи Джонсона по имени математика, давшего её простое решение. Это решение и излагается ниже. Будем говорить, что один порядок лучше другого, если соответствующее ему общее время обработки меньше, и что порядки равноценны, если времена обработки совпадают.
Решение данной задачи начнём со следующих рассуждений. Зафиксируем произвольный поря-док поступления деталей. Без ограничения общности можно считать, что это порядок 1, 2, …, n. По-ложим
Aj = τ 1 j, Bj = τ 2 j (j = 1, 2, …, n). (1)
Пусть k – произвольный номер от 1 до n –1. Наряду с исходным порядком обработки деталей рассмот-рим новый порядок, отличающийся перестановкой двух соседних – k -ой и (k +1)-ой – деталей: 1, …, k +1, k, …, n. Рассмотрим три взаимоисключающих условия:
min{ Ak, Bk +1} < min{ Ak +1, Bk }, (2a)
min{ Ak, Bk +1} > min{ Ak +1, Bk }. (2b)
min{ Ak, Bk +1} = min{ Ak +1, Bk }. (2с)
Рассматриваемое ниже решение задачи основано на следующем центральном утверждении, доказа-тельство которого приводится ниже.
Утверждение 1. Исходный порядок лучше нового тогда и только тогда, когда выполнено нера-венство (2a). Новый порядок лучше исходного тогда и только тогда, когда выполнено неравенство (2b). Порядки равноценны тогда и только тогда, когда выполнено равенство (2с).
Очевидно, что 3-я часть утверждения непосредственно следует из 1-й и 2-й. Очевидно также, что 1-я и 2-я части эквивалентны – одна следует из другой просто при перенумерации деталей (когда новый и старый порядки меняются местами, неравенства (2a) и (2b) переходят друг в друга). Поэтому доказывать придётся только 1-ю часть утверждения.
Рассмотрим следствия из пока не доказанного утверждения 1. Среди 2 n чисел A 1, …, An, B 1, …, Bn есть минимальное. Возможны два случая:
а) минимальным числом среди них является одно из чисел A 1, …, An;
б) минимальным числом среди них является одно из чисел B 1, …, Bn и не является ни одно из чисел A 1, …, An (уточнение нужно для полного разделения случаев а) и б)).
Рассмотрим сначала случай а). Пусть номер минимального числа больше 1. Тогда он может быть записан как k +1, где k – число от 1 до n –1. Тогда выполняется неравенство (2b) или равенство (2с), а это и значит – в силу утверждения 1 – что перестановка k -ой и (k +1)-ой детали либо уменьшает общее время, либо (в случае равенства (2с)) не меняет его. Поэтому всегда имеет смысл деталь с ми-нимальным временем обработки на 1-м станке поменять в очереди с соседней слева (т.е. продвинуть её к началу). Рассуждая аналогично, путём конечного числа транспозиций ставим эту деталь на первое место.
Рассмотрим теперь случай б). Пусть номер минимального числа равен k, где k – число от 1 до n –1. В этом случае опять выполняется неравенство (2b) или равенство (2с). Значит (в силу утвержде-ния 1) опять целесообразно поменять местами k -ю и (k +1)-ю детали. Но при этом деталь с минимальным временем обработки на 2-м станке сдвинется с k -го на (k +1)-е место. Продолжая этот процесс, путём конечного числа транспозиций поставим деталь с минимальным временем обработки на 2-м станке на последнее место n.
Итак, в любом случае определено место одной детали – либо в начале, либо в конце списка. Те-перь можно рассмотреть оставшиеся детали, считая без ограничения общности, что в случае а) они имеют номера от 2 до n (номер уже «поставленной» детали считаем равным 1), а в случае б) они имеют номера от 1 до n –1 (номер уже «поставленной» детали считаем равным n). Точно теми же рассуждениями отправляем одну из этих деталей (с минимальным временем обработки) в начало или в конец списка, уменьшая при этом общее время. Таким образом, после любого числа шагов рассмот-ренного вида получаем (с учётом указанной выше нумерации), что для деталей, передвигаемых в на-чало списка, выполняются условия:
1) A 1 ≤ A 2 ≤ …≤ As; 2) Ai ≤ Bi (i = 1, …, s), (3a)
а для деталей, передвигаемых в конец списка, выполняются условия
1) Bt ≥ … ≥ Bn -1 ≥ Bn; 2) Bi > Ai (i = t, …, n). (3b)
Процедура заканчивается, когда все детали войдут в указанный список. По построению и с учётом (3a) и (3b) можно сказать, что в результате все детали разбиты на две группы: детали, для которых τ 1 i ≤ τ 2 i, и детали, для которых τ 1 i > τ 2 i. Детали 1-ой группы упорядочены в порядке возрастания τ 1 i; дета-ли 2-ой группы упорядочены в порядке убывания τ 2 i; сначала обрабатываются детали 1-й группы, а затем – 2-ой группы. Таким образом, существует номер m, такой что
A 1 ≤ A 2 ≤ …≤ Am, Ai ≤ Bi (i = 1, …, m), (4a)
Bm +1 ≥ … ≥ Bn -1 ≥ Bn, Bi > Ai (i = m +1, …, n) (4b)
(случаи m =0 или m = n, т.е. случаи пустоты одной группы, не исключаются).
Поскольку мы исходили из произвольной перестановки деталей, и на каждом шаге процедуры новая перестановка либо становилась лучше предыдущей, либо оставалась равноценной ей, то тем са-мым доказано следующее
Утверждение 2. Из любой перестановки с помощью транспозиций соседних деталей можно по-лучить некоторую перестановку, удовлетворяющую условиям (4), которая будет лучше или равноцен-на исходной.
Утверждение 3. Любые две перестановки, удовлетворяющие условиям (4), равноценны.
Доказательство. Номер m и сами группы условиями задачи определяется однознач-но. 1-ая группа деталей разбивается на непересекающиеся подмножества G 1, …, Gd, такие что
< … < 
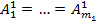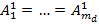; (5a)
2-ая группа деталей разбивается на непересекающиеся подмножества H 1, …, He, такие что
> … > 
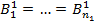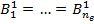. (5b)
Оба разбиения также определяется только условиями задачи. Все различия между перестановками, удовлетворяющими (4), состоят в произвольности порядка деталей внутри групп Gi и Hj. Пусть π 1 и π 2 – любые две перестановки элементов в группе G 1. От π 1 к π 2 можно перейти транспозициями сосед-них деталей. Поскольку внутри группы G 1
Ak = Ak +1 =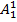 
, Ak ≤ Bk, Ak +1≤ Bk +1, (6)
то из (6) следует, что
min{ Ak, Bk +1} = min{ Ak +1, Bk } = 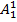. (7)
Поэтому, в силу утверждения 1, любые две перестановки деталей, отличающиеся только внутри груп-пы G 1, равноценны. Аналогичные рассуждения для других групп завершают доказательство утверж-дения 3 ■
Утверждения 2 и 3 вместе означают, что любая перестановка деталей, удовлетворяющая услови-ям (4), является оптимальной. (Заметим, что именно таковой является 2-ая перестановка в примере 1.) Подобная перестановка легко находится непосредственно по исходным данным. Никакого специаль-ного алгоритма в данном случае не требуется. Тот факт, что в рассматриваемой задаче удалось полу-чить такой простой явный ответ, является для дискретных задач скорее исключением, чем правилом. Уже в случае трех станков (аналогичная задача, в которой требуется последовательная обработка на трех станках) в общем случае такого простого ответа нет.
