Если в канале нет помех, то потери информации не будет. Если источник имеет N различных символов, а основание кода равно m, то длина кодовой группы равна числу кодовых символов. Пусть длина i -й кодовой группы ni сопоставляется сообщению Ai, веро-
ятность которого p(Ai). Средняя длина кодовой группы

зависит от того, как закодировано сообщение. Вообще говоря, необходимо, чтобы

Информация на символ кода максимальна, если символы кода равновероятны и независимы, тогда она равна log m.
Минимальная длина i -й кодовой группы i-го сообщения находится как

где log m – информация на символ кода; log p(Ai) – информация i -го сообщения.
Тогда
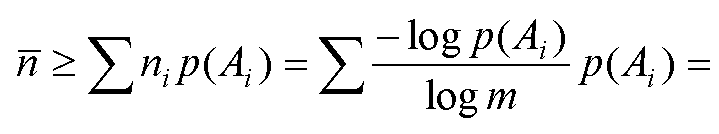

46 Напишите о кодировании источников сообщений с равновероятными символами
Пусть имеется источник сообщений 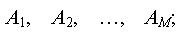

энтропия на сообщение H(A) = log N.
Так как код равномерный, то все кодовые комбинации будут иметь одинаковую длину

Если по каналу в секунду передаётся VM символов кода или VM / n кодовых комбинаций, то

47 Напишите о кодировании источников сообщений с неравновероятными независимыми символами без помех
имеется источник сообщений 

Если выбрать равномерный код, то

т. е. для неравновероятных символов равномерный код переносит меньшую информацию, чем пропускная способность, т. е. он не оптимален.
Скорость передачи информации можно увеличить путём укорочения длины кодовых комбинаций
48 Напишите о кодировании в каналах с помехами
Пропускная способность

где (H(x)–H(x/y)) – информация, которая переносится в КС одним символом; VМ – скорость модуляции; H(x/y) – потери; H(x) – энтропия КС; Vп = VМH(x) – скорость передачи информации по КС; Vпотерь = VМH(x/у).
Пропускная способность – это максимальная скорость передачи информации по КС, где максимум берётся по всем возможным законам распределения сообщений на выходе ИС

49 Напишите о первой прямой теореме Шеннона
В канале связи с помехами всегда можно получить сколь угодно малую вероятность ошибочного приёма сообщений, если выполняется условие

Д о к а з а т е л ь с т в о. Рассмотрим проблемы, возникающие при передаче дискретных сообщений по каналам с шумом
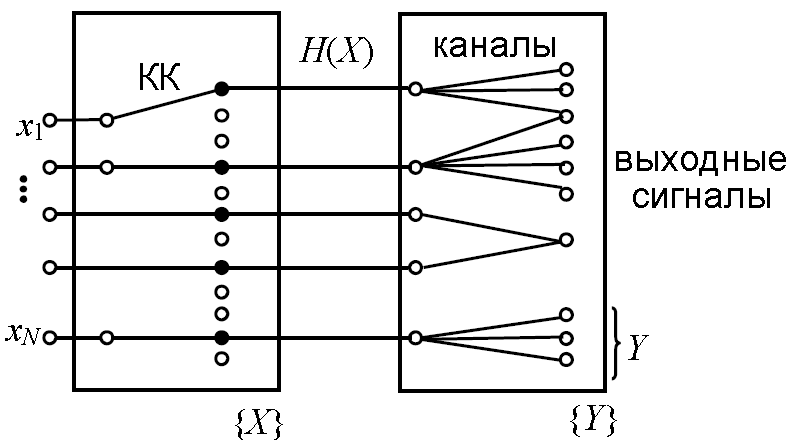
На вход КК поступает одна из N0 последовательностей символов, которую надо передать по каналу связи без ошибок. Число возможных последовательностей резко увеличивается, но КК работает только с N0 из них разрешёнными.
Проблема состоит в том, чтобы выяснить, возможно ли такое размещение N0 переданных последовательностей среди возможных N входных и разбиение на группы, чтобы вероятность ошибки не превышала сколь угодно малой заданной величины.
50 Напишите обратную теорему Шеннона
Обратная теорема ограничивает максимальную степень сжатия, достигаемую с помощью кодирования без потерь. В применении к побуквенному кодированию, описывает ограничение на среднюю длину кодового слова для любого разделимого кода.
Для любого разделимого кода с длинами {\displaystyle w_{1},w_{2},...,w_{K}} средняя длина сообщений больше или равна энтропии источника {\displaystyle U}, нормированный на двоичный логарифмот числа букв {\displaystyle D} в алфавите кодера:

51 Напишите о второй теореме Шеннона
Вторая теорема гласит, что увеличения избыточности до бесконечности не требуется при снижении Pош до нуля.
Теорема. При условии Vист≤C среди кодов, обеспечивающих сколь угодно малую Рош, существует код, при котором скорость передачи информации сколь угодно близка к скорости создания информации:

Наличие шума в информационной системе приводит к нарушению соответствия между входным и выходным сигналами

Были получены наиболее важные результаты теории информации, которые можно назвать крупными научными открытиями.
К ним относятся:
– первая теорема Шеннона (прямая и обратная);
– вторая теорема Шеннона.
Из первой теоремы следует, что как бы ни был сильным шум, можно создать условия, при которых возможна передача информации при сколь угодно малой вероятности ошибки.
Из второй теоремы следует, что не потребуется до бесконечности понижать скорость передачи при повышении требований к малости ошибки.
52 Напишите применение теорем Шеннона для непрерывных каналов

Если М – число каналов продолжительностью T, то скорость передачи информации равна [бит/с]


Найдём число сообщений M. Вероятность того, что точка находится внутри объёма Vштр





53 Напишите основную задачу помехоустойчивого кодирования
Основной задачей помехоустойчивого кодирования является обеспечение высокой достоверности передаваемых данных за счет применения устройств кодирования/декодирования в составе системы передачи цифровой информации, включающей источник данных, кодер канала, модулятор, физический канал, демодулятор и детектор, декодер канала, приемник данных.
В общем случае процедура кодирования представляет собой преобразование одного алфавита в другой.
Для реализации возможности примененияна приемной стороне режимов обнаружения и исправления ошибок в кодовые комбинации на передающей стороне необходимо ввести избыточность. Такие коды называются кодами с избыточностью или помехоустойчивыми (корректирующими) кодами. Избыточность чаще всего вводится путем добавления к безызбыточной КК так называемых проверочных символов.
54 Напишите об обозначениях для помехоустойчивых кодов
Приняты следующие обозначения для помехоустойчивых кодов:
n – значность кода, т. е. общее число символов в избыточной кодовой комбинации;
k – число информационных символов, т. е. число символов в первоначальной безызбыточной кодовой комбинации;
r – число проверочных символов, т. е. число символов, добавляемых к первоначальной безызбыточной кодовой комбинации, причем
n = k + r.
Помехоустойчивый код значности nс числом k информационных сим- волов обозначается как (n,k)-код.
55 Напишите о минимальном Хеммингово расстоянии dmin
Важной характеристикой помехоустойчивого кода является так называемое минимальное Хеммингово расстояние dmin, определяемое как минимальное расстояние в пространстве Хемминга среди всех возможных расстояний между двумя любыми КК данного кода.


Пример двух расстояний: 100 → 011 имеют расстояние 3 (красные рёбра); 010 → 111 имеют расстояние 2 (синие рёбра).
Одной из важных задач в теории помехоустойчивого кодирования является задача максимизации минимального Хеммингова расстояния dmin при фиксированных значениях остальных параметров. Наглядный подход к уяснению данной задачи может быть показан при рассмотрении геометрического смысла кодирования
56 Напишите об энергетическом выигрыше от кодирования
Ещё одной важной и широко применяемой характеристикой помехоустойчивого кода является энергетический выигрыш от кодирования (ЭВК), определяемый как отношение превышений энергии сигнала на бит к спектральной мощности шума при отсутствии и при наличии кодирования




Графическая интерпретация оценки ЭВК
57 Напишите использование помехоустойчивых кодов в режиме обнаружения и в режиме исправления ошибок.
Помехоустойчивые коды могут использоваться в режиме обнаружения и в режиме исправления ошибок.

58 Приведите графическую интерпретацию оценки энергетического выигрыша от кодирования
Ещё одной важной и широко применяемой характеристикой помехоустойчивого кода является энергетический выигрыш от кодирования (ЭВК), определяемый как отношение превышений энергии сигнала на бит к спектральной мощности шума при отсутствии и при наличии кодирования




Графическая интерпретация оценки ЭВК
59 Напишите формулы пропускной способности

60 Приведите виды аналоговых систем модуляции
4) Амплитудная модуляция (АМ)
5) 
6) Фазовая модуляция (ФМ)
7) 
3) Частотная модуляция (ЧМ)

4) Однополосная модуляция (ОМ)

{\displaystyle {\frac {H\left(U\right)}{\log _{2}D}}\leq E_{U}w\left(U\right)}






