Тема 1. Систематические погрешности.
1. Методом амперметра-вольтметра измеряется сопротивление RХ. Показания амперметра IА = 0,03 А, показания вольтметра UV = 9 В. Известно, что сопротивления амперметра и вольтметра составляют соответственно RA = 3 Ом, RV = 30 кОм. Нарисовать оптимальную схему измерения, определить величину относительной методической погрешности, найти исправленный результат измерения.
2. 
Сопротивление RХ измеряется с помощью четырехплечего моста, в котором номинальные значения резисторов R2 и R3 равны 1000 Ом. Равновесие моста достигается при R /1 = 1000,4 Ом. Для устранения систематической погрешности производится смена местами резисторов RХ и R1. В этом случае равновесие моста достигается при R //1 = 1000,2 Ом. Определить RХ и действительное соотношение плеч моста n=R2/R3. Классифицировать метод измерения RХ и метод устранения систематической погрешности.
Тема 2. Случайные погрешности.
1. В результате испытаний милливольтметра установлено, что 60% его погрешностей не превосходят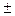 
20 мВ. Погрешности распределены по равновероятному закону с нулевым математическим ожиданием. Определить границы доверительного интервала погрешности при доверительной вероятности Рд = 0,95. Найти СКП.
2. В результате поверки амперметра установлено, что 50% его погрешностей не превосходят 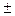10 мА. Считая, что погрешность распределена по нормальному закону с нулевым математическим ожиданием, найти симметричный доверительный интервал для погрешности, вероятность попадания в который равна 0,95.
3. Для случайной погрешности измерения напряжения, распределенной по нормальному закону с нулевым математическим ожиданием определить среднюю квадратическую погрешность S, если известно, что граница доверительного интервала погрешности 
=10мВ при доверительной вероятности Рд = 0,7.
4. Известно, что границы доверительного интервала случайной погрешности, распределенной по треугольному закону 
. Определить границы существования погрешности и ее СКО.
Тема 3. Погрешности СИ.
1. Построить графики зависимости абсолютной и относительной погрешностей от измеряемой мощности для ваттметра с пределом шкалы 1,0 Вт, класса точности 1,0. Количество расчетных точек графиков – не менее 5. Повторить задачу для прибора с классом точности 1,0/0,2.
2. 
Определить величину измеряемого напряжения, если известно, что оно измерено с погрешностью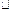 
U=1,0 В вольтметром с пределом измерения Uшк = 100В и классом точности 1,0/0,2. Повторить решение задачи для прибора с классом точности 
.
3. Определить эксплуатационную погрешность измерения силы тока, если известно, что амперметр с пределом шкалы 100 мА; класса точности 2,0 показал 80,25 мА. Измерения проводились при напряженности внешнего магнитного поля 200А/м и напряжении питания 200 В. Дополнительная погрешность амперметра не превышает половины основной при изменении напряженности магнитного поля на каждые 100 А/м относительно нормального значения напряженности поля 100 А/м, а дополнительная погрешность прибора за счет напряжения питания не превышает основной при изменении питания на каждые 20 В относительно нормального значения 220 В. Записать результат измерения.
Тема 4. Обработка многократных равноточных измерений.
1. Известны результаты многократных равноточных наблюдений мощности сигнала в Вт.: 1,1; 1,2; 1,3; 1,4; 1,0; 1,8; 1,2; 1,2; 1,1; 1,3. Определить результат измерения, СКП отдельного измерения, записать результат измерения при доверительной вероятности Рд =0,95.
2. Определить наличие и удалить, в случае необходимости, промахи из результатов многократных равноточных измерений напряжения в мВ: 20,0; 20,5; 20,5; 22,0; 18,0; 19,5; 20,0; 24,0; 25,5; 19,5.
3. При поверке вольтметра с помощью образцовой меры 20В показания поверяемого прибора в вольтах были: 20,15; 20,50; 20,35; 20,25; 20,05; 20,35; 20,28; 20,24; 20,26; 20,18. Определить систематическую, среднеквадратическую и максимальную погрешность поверяемого вольтметра.
Тема 5. Обработка косвенных измерений.
1. Определить результат и погрешность косвенного измерения напряжения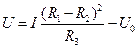 
по результатам прямых измерений: R1=(100 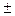1) Ом, R2=(51 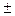0,5)Ом, R3=2,4 Ом, 
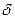R3= 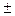1%; U0=2В измерено вольтметром класса точности 1,0 с пределом шкалы 3В. I=9 мА измерено амперметром класса точности 
1,5 с пределом шкалы 10 мА. Записать результат измерения.
2. 
Емкость 
С=С2-С1 определена по результатам прямых измерений: С1=94,8 пФ, С2=102,3 пФ. Систематические погрешности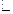 
с1=0,9 пФ; 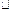с2=1,1 пФ. СКО случайных погрешностей, распределенных по гауссовому закону 
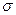с1= 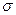с2=0,5 пФ, коэффициент корреляции rij=0. Определить результат и погрешность измерения С. Записать результат измерения.
Тема 6. Суммирование погрешностей.
1. При измерении напряжения получено среднее арифметическое многократных измерений 
=115,73 мВ; составляющие случайной погрешности S1=1.2 мВ; S2=0,8мВ; 
мВ, коэффициент корреляции 
, составляющие неисключенной систематической погрешности (НСП) 
1=0,8мВ; 2=0,6 мВ. Записать результат измерения при доверительной вероятности Рд=0,9.
2. При измерении сопротивления цифровым омметром с пределом шкалы 1000 Ом показания прибора составили 910 Ом. Из паспортных данных прибора известно, что систематическая погрешность составляет 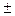(0,2% + стоимость 1 единицы младшего разряда кода R), дополнительная температурная погрешность при рабочей температуре 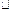Rt= 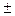1 Ом, среднеквадратическое отклонение случайной погрешности S=0,7 Ом. Записать результат измерения.
Тема 7. Поверка, калибровка.
1. При поверке милливольтметра класса точности 
0=2,0 с пределом шкалы Uшкп=100 мВ используется образцовый прибор с Uшк 0=300 мВ класса точности 0=0,1. В результате поверки получены следующие результаты:
| Un | ||||||
| Uо | 19,05 | 39,1 | 59,0 | 81,0 | 99,01 |
Определить — годен ли поверяемый прибор.
2. При поверке частотомера с помощью стандарта частоты 1 кГц были получены следующие результаты: 1001; 1002; 1001; 999; 1000,5; 1001,5; 1001,5; 1002; 1001 Гц. Определить систематическую погрешность и СКО случайной погрешности частотомера. Присвоить ему класс точности, считая. что погрешность носит в основном мультипликативный характер.
Рекомендуемая литература:
5. Эрастов В.Е. «Метрология, стандартизация и сертификация», — Томск, Издательство ТУСУР, 2005.
6. Отчалко В.Ф. Метрология, стандартизация и сертификация: Учебное пособие. – Томск: ТМЦДО, 2010
7. Отчалко В.Ф, Сидоров Ю.К., Эрастов В.Е. «Измерительная техника и датчики». Учебное методическое пособие. — Томск, ТМЦДО, 2004.
8. Отчалко В.Ф. Метрология, стандартизация и сертификация: Учебное методическое пособие. – Томск: ТМЦДО, 2010
9. Федеральный закон РФ «О техническом регулировании» №184-ФЗ от 27.12.2002г. с последующими изменениями.
10. Федеральный закон РФ «Об обеспечении единства измерений» №102 от 26.06.2008г.
Приложение
Статистические таблицы
Таблица П.1 — Интегральная функция нормального распределения
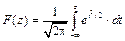
| z | 0.08 | 0.06 | 0.04 | 0.02 | 0.00 |
| –3.3 | 0.00036 | 0.00039 | 0.00042 | 0.00045 | 0.00048 |
| –3.2 | 0.00052 | 0.00056 | 0.00060 | 0.00064 | 0.00069 |
| –3.1 | 0.00074 | 0.00079 | 0.00085 | 0.00090 | 0.00097 |
| –3.0 | 0.00104 | 0.00111 | 0.00118 | 0.00126 | 0.00135 |
| –2.9 | 0.0014 | 0.0015 | 0.0016 | 0.0017 | 0.0019 |
| –2.8 | 0.0020 | 0.0021 | 0.0023 | 0.0024 | 0.0026 |
| –2.7 | 0.0027 | 0.0029 | 0.0031 | 0.0033 | 0.0035 |
| –2.6 | 0.0037 | 0.0039 | 0.0041 | 0.0044 | 0.0047 |
| –2.5 | 0.0049 | 0.0052 | 0.0055 | 0.0059 | 0.0062 |
| –2.4 | 0.0066 | 0.0069 | 0.0073 | 0.0078 | 0.0082 |
| –2.3 | 0.0087 | 0.0091 | 0.0096 | 0.0102 | 0.0107 |
| –2.2 | 0.0113 | 0.0119 | 0.0125 | 0.0132 | 0.0139 |
| –2.1 | 0.0146 | 0.0154 | 0.0162 | 0.0170 | 0.0179 |
| –2.0 | 0.0188 | 0.0197 | 0.0207 | 0.0217 | 0.0228 |
| –1.9 | 0.0239 | 0.0250 | 0.0262 | 0.0274 | 0.0287 |
| –1.8 | 0.0301 | 0.0314 | 0.0329 | 0.0344 | 0.0359 |
| –1.7 | 0.0375 | 0.0392 | 0.0409 | 0.0427 | 0.0446 |
| –1.6 | 0.0465 | 0.0485 | 0.0505 | 0.0556 | 0.0578 |
| –1.5 | 0.0571 | 0.0594 | 0.0618 | 0.0643 | 0.0668 |
| –1.4 | 0.0694 | 0.0721 | 0.0749 | 0.0778 | 0.0808 |
| –1.3 | 0.0838 | 0.0869 | 0.0901 | 0.0934 | 0.0968 |
| –1.2 | 0.1003 | 0.1038 | 0.1075 | 0.1112 | 0.1151 |
| –1.1 | 0.1190 | 0.1230 | 0.1271 | 0.1314 | 0.1357 |
| –1.0 | 0.1401 | 0.1446 | 0.1492 | 0.1539 | 0.1587 |
| –0.9 | 0.1635 | 0.1685 | 0.1736 | 0.1788 | 0.1841 |
| –0.8 | 0.1894 | 0.1949 | 0.2005 | 0.2061 | 0.2119 |
| –0.7 | 0.2177 | 0.2236 | 0.2297 | 0.2358 | 0.2420 |
| –0.6 | 0.2483 | 0.2546 | 0.2611 | 0.2678 | 0.2743 |
| –0.5 | 0.2810 | 0.2877 | 0.2946 | 0.3015 | 0.3085 |
| –0.4 | 0.3156 | 0.3288 | 0.3300 | 0.3372 | 0.3446 |
| –0.3 | 0.3520 | 0.3594 | 0.3669 | 0.3745 | 0.3821 |
| –0.2 | 0.3897 | 0.3974 | 0.4052 | 0.4129 | 0.4207 |
| –0.1 | 0.4286 | 0.4364 | 0.4443 | 0.4522 | 0.4602 |
| –0.0 | 0.4681 | 0.4761 | 0.4840 | 0.4920 | 0.5000 |
Окончание табл. П.1
| z | 0.00 | 0.02 | 0.04 | 0.06 | 0.08 |
| +0.0 | 0.5000 | 0.5080 | 0.5160 | 0.5319 | |
| +0.1 | 0.5398 | 0.5478 | 0.5557 | 0.5636 | 0.5714 |
| +0.2 | 0.5793 | 0.5871 | 0.5948 | 0.6026 | 0.6103 |
| +0.3 | 0.6179 | 0.6255 | 0.6331 | 0.6406 | 0.6480 |
| +0.4 | 0.6554 | 0.6628 | 0.6700 | 0.6772 | 0.6844 |
| +0.5 | 0.6915 | 0.6985 | 0.7054 | 0.7123 | 0.7190 |
| +0.6 | 0.7257 | 0.7324 | 0.7389 | 0.7454 | 0.7517 |
| +0.7 | 0.7580 | 0.7642 | 0.7704 | 0.7764 | 0.7823 |
| +0.8 | 0.7881 | 0.7939 | 0.7995 | 0.8051 | 0.8106 |
| +0.9 | 0.8159 | 0.8212 | 0.8264 | 0.8315 | 0.8365 |
| +1.0 | 0.8413 | 0.8461 | 0.8505 | 0.8554 | 0.8599 |
| +1.1 | 0.8643 | 0.8686 | 0.8729 | 0.8770 | 0.8810 |
| +1.2 | 0.8849 | 0.8888 | 0.8925 | 0.8962 | 0.8997 |
| +1.3 | 0.9032 | 0.9066 | 0.9099 | 0.9131 | 0.9162 |
| +1.4 | 0.9192 | 0.9222 | 0.9251 | 0.9279 | 0.9306 |
| +1.5 | 0.9332 | 0.9357 | 0.9382 | 0.9406 | 0.9429 |
| +1.6 | 0.9452 | 0.9474 | 0.9495 | 0.9515 | 0.9535 |
| +1.7 | 0.9552 | 0.9573 | 0.9591 | 0.9608 | 0.9625 |
| +1.8 | 0.9641 | 0.9656 | 0.9671 | 0.9686 | 0.9699 |
| +1.9 | 0.9713 | 0.9726 | 0.9738 | 0.9750 | 0.9761 |
| +2.0 | 0.9773 | 0.9783 | 0.9793 | 0.9803 | 0.9812 |
| +2.1 | 0.9821 | 0.9830 | 0.9838 | 0.9846 | 0.9854 |
| +2.2 | 0.9861 | 0.9868 | 0.9875 | 0.9881 | 0.9887 |
| +2.3 | 0.9893 | 0.9898 | 0.9904 | 0.9909 | 0.9913 |
| +2.4 | 0.9918 | 0.9922 | 0.9927 | 0.9931 | 0.9934 |
| +2.5 | 0.9938 | 0.9941 | 0.9945 | 0.9948 | 0.9951 |
| +2.6 | 0.9953 | 0.9956 | 0.9959 | 0.9961 | 0.9963 |
| +2.7 | 0.9965 | 0.9967 | 0.9969 | 0.9971 | 0.9973 |
| +2.8 | 0.9974 | 0.9976 | 0.9977 | 0.9979 | 0.9980 |
| +2.9 | 0.9981 | 0.9983 | 0.9984 | 0.9985 | 0.9986 |
| +3.0 | 0.99865 | 0.99874 | 0.99882 | 0.99889 | 0.99896 |
| +3.1 | 0.99903 | 0.99910 | 0.99915 | 0.99921 | 0.99926 |
| +3.2 | 0.99931 | 0.99936 | 0.99940 | 0.99954 | 0.99948 |
Таблица П.2 — Значения допускаемых нормированных отклонений
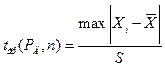
| Число наблюдений | Уровень значимости g (доверительная вероятность Р) | ||||
| g = 0.001 (P = 0.999) | g = 0.005 (P = 0.995) | g = 0.01 (P = 0.99) | g = 0.05 (P = 0.95) | g = 0.1 (P = 0.90) | |
| 1.414 | 1.414 | 1.414 | 1.414 | 1.412 | |
| 1.732 | 1.730 | 1.728 | 1.710 | 1.689 | |
| 1.994 | 1.982 | 1.972 | 1.917 | 1.869 | |
| 2.212 | 2.183 | 2.161 | 2.067 | 1.996 | |
| 2.395 | 2.344 | 2.310 | 2.182 | 2.093 | |
| 2.547 | 2.476 | 2.431 | 2.273 | 2.172 | |
| 2.677 | 2.586 | 2.532 | 2.349 | 2.238 | |
| 2.788 | 2.680 | 2.616 | 2.414 | 2.294 | |
| 2.884 | 2.760 | 2.689 | 2.470 | 2.343 | |
| 2.969 | 2.830 | 2.753 | 2.519 | 2.387 | |
| 3.044 | 2.892 | 2.809 | 2.563 | 2.426 | |
| 3.111 | 2.947 | 2.859 | 2.602 | 2.461 | |
| 3.171 | 2.997 | 2.905 | 2.638 | 2.494 | |
| 3.225 | 3.042 | 2.946 | 2.670 | 2.523 | |
| 3.274 | 3.083 | 2.983 | 2.701 | 2.551 | |
| 3.320 | 3.120 | 3.017 | 2.728 | 2.577 | |
| 3.361 | 3.155 | 3.049 | 2.754 | 2.601 | |
| 3.400 | 3.187 | 3.079 | 2.779 | 2.623 | |
| 3.436 | 3.217 | 3.106 | 2.801 | 2.644 | |
| 3.469 | 3.245 | 3.132 | 2.823 | 2.664 | |
| 3.500 | 3.271 | 3.156 | 2.843 | 2.683 | |
| 3.529 | 3.295 | 3.179 | 2.862 | 2.701 | |
| 3.556 | 3.318 | 3.200 | 2.880 | 2.718 | |
| 3.582 | 3.340 | 3.220 | 2.897 | 2.734 | |
| 3.606 | 3.360 | 3.239 | 2.913 | 2.749 | |
| 3.629 | 3.380 | 3.258 | 2.929 | 2.764 | |
| 3.651 | 3.399 | 3.275 | 2.944 | 2.778 | |
| 3.672 | 3.416 | 3.291 | 2.958 | 2.792 |
Таблица П.3 — Значение коэффициента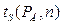 
для различных доверительных вероятностей (распределение Стьюдента)
| n | 0.8 | 0.9 | 0.95 | 0.98 | 0.99 | 0.999 |
| 3.078 | 6.314 | 12.706 | 31.821 | 63.657 | 636.619 | |
| 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 31.598 | |
| 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 12.941 | |
| 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 8.610 | |
| 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 6.859 | |
| 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 5.959 | |
| 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 5.405 | |
| 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 5.041 | |
| 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 4.781 | |
| 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 4.587 | |
| 1.363 | 1.796 | 2.201 | 2.718 | 3.103 | 4.487 | |
| 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 4.318 | |
| 1.350 | 1.771 | 2.160 | 2.850 | 3.012 | 4.221 | |
| 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 4.140 | |
| 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 4.073 | |
| 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 4.015 | |
| 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.965 | |
| 1.330 | 1.734 | 2.103 | 2.552 | 2.878 | 3.992 | |
| 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.883 | |
| 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.850 | |
| 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.819 | |
| 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.792 | |
| 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.767 | |
| 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.745 | |
| 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.725 | |
| 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.707 | |
| 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.690 | |
| 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.674 | |
| 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.659 | |
| 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.646 | |
| 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 3.551 | |
| 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 3.460 | |
| 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 3.373 | |
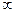
| 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 3.291 |
