НАДІЙНІСТЬ ТА ДІАГНОСТУВАННЯ
для студентів 3 курсу
напряму підготовки: 6.050201 «Системна інженерія»
факультету кібернетики
Херсон -2013
Конспект лекцій з дисципліни «Надійність та діагностування», для напряму підготовки 6.050201 ”Системна інженерія”
Укладач: к.т.н., доцент Касап А.М.,кількість сторінок - 76
Затверджено
на засіданні каф. ТК.
протокол № ____ від
«» ________ 2013 р.
Зав. кафедри д.т.н., проф. В.В.Марасанов
Відповідальний за випуск д.т.н., проф. В.В.Марасанов
ЗМІСТ
Вступ……..........................................................................5
Розділ І Основи теорії надійності …………..………6
1 Основні поняття і визначення теорії надійності……...6
1.1 Основні поняття і визначення теорії надійності………….6
1.2 Безвідмовність і її показники………………….………..….7
1.3 Основні закони розподілу часу безвідмовної роботи.. …15
1.4 Основні моделі надійності апаратури….. ……….………19
1.5 Чинники, що впливають на показники надійності………22
2 Методи підвищення надійності…...………………….25
2.1 Загальні методи підвищення надійності…..…………….25
2.2 Підвищення надійності шляхом впровадження
мікроелектроніки.................................................................26
2.3 Підвищення надійності шляхом резервування
апаратури ………………………………………………….27
2.4 Безвідмовність апаратури при загальному і
pоздільному резервуванні……………………………..….28
3 Розрахунок надійності апаратури…..………………...33
3.1 Аналітичний розрахунок надійності...…………..………33
3.2 Види аналітичного розрахунку надійності.……………..35
3.3 Розрахунок надійності за статистичними даними..…….38
4 Розрахунок запасних частин……...…………………..42
4.1 Призначення і типи запасних частин…...………...……....42
4.2 Вибір номенклатури запасних частин....…………………44
4.3 Розрахунок кількості запасних частин…………………...45
Розділ ІІ Технічна діагностика...…………………..49
5 Методи і алгоритми технічної діагностики….………49
5.1 Загальні відомості про технічну діагностику...…………..49
5.2 Технічні засоби діагностування….………………………..50
5.3 Показники діагностування…...…………………………….52
5.4 Методи діагностування…………………………………….55
5.5 Функціональні схеми систем діагностування...………….56
5.6 Функціональна модель апаратури…..……………………..59
5.7 Таблиця станів функціональної моделі...…………………60
5.8 Алгоритми перевірки технічного стану об’єктів...……….62
5.9 Алгоритми пошуку несправностей в об’єктах.………….64
6 Діагностування об’єктів обчислювальної техніки….69
6.1 Технічні засоби діагностування об’єктів
обчислювальної техніки……………………………...……69
6.2 Логічні аналізатори.……………………………………......69
6.3 Сигнатурні аналізатори..……………………………….....72
Література.........................................................................75
ВСТУП
Ефективність будь-якої технічної системи характеризується, перш за все, її технічними параметрами і надійністю. У свою чергу, надійність як складна властивість залежно від призначення системи або об'єктів складається з поєднання властивостей безвідмовності, довговічності, ремонтопридатності і збережливості, залежить від умов використання технічної системи.
При створенні складних систем виникає гостра необхідність вирішення завдань їх технічної діагностики практично на всіх етапах – проектування, виробництва і експлуатації. Застосування методів і засобів технічної діагностики надає істотний вплив на ефективність використання технічних систем.
Предметом вивчення навчальної дисципліни “Надійність та діагностування” є основні поняття і визначення теорії надійності, методи підвищення надійності, розрахунок надійності апаратури, розрахунок запаснихчастин, методи і алгоритми технічної діагностики, технічні засоби діагностики технічних об’єктів загалом і засобів обчислювальної техніки в частковості.
Розділ І. Основи теорії надійності
1 Основні поняття і визначення теорії надійності
Основні поняття і визначення теорії надійності.
Надійність - властивість oб’єкта зберігати в часі у встановлених межах значення всіх параметрів, що характеризують його здатність виконувати потрібні функцій в заданих режимах і умовах застосування, технічного обслуговування, ремонтів, зберігання і транспортування
(ГОСТ 27.002-82).
Надійність - складна властивість технічного об'єкту. Вона включає простіші властивості. Це складові частини або сторони надійності. До сторін надійності відносять:
· безвідмовність;
· ремонтопридатність;
· довговічність;
· збереженність.
Безвідмовність – властивість об'єкту безперервно зберігати працездатність протягом деякого часу або деякого напрацювання.
Ремонтопридатність – властивість об'єкту, яка полягає в пристосованості його до попередження і виявлення відмов і відновлення працездатності або шляхом проведення ремонту, або шляхом заміни комплектуючих елементів, що відмовили.
Довговічність – властивість об'єкту зберігати працездатність до настання граничного стану. Граничний стан об'єкту – це стан при якому подальша експлуатація об'єкту неможлива або економічно недоцільна.
Збереженність – властивість об'єкту зберігати працездатність під час зберігання або транспортування.
Працездатність – такий стан об'єкту при якому він здатний виконувати задані функції, задовольняючи вимогам нормативно-технічної документації.
В основі поняття надійності об'єкту лежить поняття його відмови. Відмова об'єкту – подія, що полягає в тому, що об'єкт або повністю, або частково втрачає свою працездатність При повній втраті працездатності виникає повна відмова, при частковій – часткова відмова.
Відмови можуть бути раптовими і поступовими. Раптовій відмові може не передувати поступове накопичення пошкоджень і він виникає раптово. Поступова відмова виникає в результаті поступового накопичення пошкоджень, головним чином унаслідок зносу і старіння матеріалів.
Відмова може бути короткочасною самоусуванною. Така відмова називається збоєм. Характерна ознака збою – те, що відновлення працездатності апаратури після виникнення збою не вимагає ремонту апаратури. Причиною збою може бути або короткочасна відмова апаратури (наприклад, залипання контакту), або короткочасно діюча перешкода, або дефекти програми.
1.2 Безвідмовність і її показники.
Поняття безвідмовності – основне поняття теорії надійності. Основною кількісною мірою безвідмовності є вірогідність безвідмовної роботи P(t) – вірогідність того, що в межах заданого напрацювання відмова об'єкту не виникає. «Напрацювання» - термін, що визначає тривалість роботи об'єкту.
Виникнення відмови є випадковою подією, тому час появи відмови - t0 також є випадкова величина (рис.1.1).
Вірогідність безвідмовної роботи можна визначити, як вірогідність того, що час роботи t0 об'єкту буде більше деякого заданого часу P(t) = P(t<t0). На практиці вірогідність безвідмовної работы часто визначають статистичним шляхом за
Рис. 1.1 Час відмови апаратури
інформацією про відмови за вибраний проміжок часу ti:
, (1.1)
де N – число однотипних об’єктів поставлених на випробування;
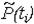ni – число об’єктів, відмовивших за час ti.
При значному числі об’єктів статистична вірогідність
спрямовується до теоретичної вірогідності.
Надійність об'єкту іноді зручніше характеризувати вірогідністю відмови:
. (1.2)
Таким чином, вірогідність появи відмови Q(t) можна розглядати як вірогідність того, що випадкова величина t0 прийме значення менше даного часу t. Це дозволяє розглядати Q(t) як функцію розподілу випадкової величини t0.
Функціональні залежності P(t) і Q(t) показані на рис.1.2.
 |
Рис. 1.2 Графіки залежності P(t) і Q(t) від часу
Статистичним шляхом вірогідність відмови знаходиться за допомогою виразу:
. (1.3)
Розрізняють об'єкти на такі, що не підлягають ремонту і ремонтовані. Показники безвідмовності цих об'єктів декілька відрізняються.
1.2.1. Безвідмовність об'єктів, що не підлягають ремонту.
У об’єктів, які не підлягають ремонту, показниками безвідмовності є:
– вірогідність безвідмовної робот - P(t);
– частота відмов - f(t);
– інтенсивність відмов - λ(t);
– среднє напрацювання на відмову - Тсер .
Під частотою відмов розуміють число відмов об'єктів (елементів) в одиницю часу, віднесене до первинного числа об'єктів (елементів) поставлених на випробування. За статистичними даними частота відмов знаходиться за допомогою виразу:
, (1.4)
де N – число об’єктів (елементів) поставлених на випробування;
ni – число об’єктів (елементів) відмовивших протягом i -го інтервалі часу - ti (рис.1.1.);
ti – величина i -го інтервала часу.
При цьому об'єкти, що відмовили в процесі випробувань, не замінюються новими і число працюючих об'єктів поступово зменшується.
Функцію частоти відмов можна записати в наступному вигляді:
Тут n(ti + Δ ti) – число об’єктів, відмовивших за час ti +Δ ti;
n(ti) - число об’єктів, відмовивших за час ti.
Якщо перейти від фіксованого часу ti до поточного t і поточний час спрямувати до нескінченності (t →∞), а інтервал часу Δ ti спрямувати до нуля, то:
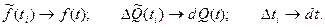
Тоді отримаємо:
. (1.5)
З виразу (5) випливає:
(1.6)
Продиференціювавши останній вираз, отримаємо:
. (1.7)
Таким чином, функція частоти відмов f(t) є похідна від функції P(t) узята із зворотним знаком. Вона характеризує швидкість зниження надійності в часі.
Оскільки Q(t) є інтегральний закон розподілу часу безвідмовної роботи t0 , то похідна від Q(t) є ніщо інше як щільність розподілу вірогідності випадкової величини t0. Тобто,
f(t) – щільність розподілу часу безвідмовної роботи.
Під інтенсивністю відмов розуміють число відмов в одиницю часу, віднесене до середнього числа об'єктів, що безвідмовно працюють в даний проміжок часу. При цьому об'єкти, що відмовили, не замінюються.
З дослідних даних ця характеристика розраховується по формулі:
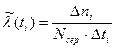, (1.8)
де 
- середнє число працездатних об’єктів в і – му інтервалі часу;
Ni - число об’єктів, працездатних на початку і – го інтервалу часу;
Ni+1 - число об’єктів, працездатних на кінець і – го інтервалу часу;
Якщо чисельник і знаменник виразу (8) розділити на величину N Δ ti, то отримаємо:
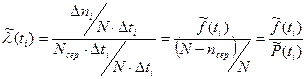. (1.9)
Тут nсер - середнє число об’єктів, відмовивших на кінець інтервалу Δ ti.
Переходячи від дискретних понять до безперервних (тобто при Δ ti →0), отримаємо:
.
Рішення цього диференціального рівняння дає основний закон надійності:
. (1.10)
Залежність інтенсивності відмов від часу експлуатації для складних технічних об'єктів показана на рис. 1.3.
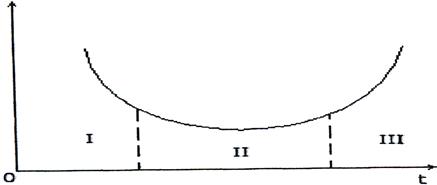
Рис. 1.3 Залежність від часу експлуатації технічних об’єктів
При експлуатації технічних об’єктів виділяють три періода (І, ІІ і ІІІ), коли інтенсивність відмов має різний характер поведінки. Протягом І періода інтенсивність відмов значна, але з часом падає. Цей період називають періодом припрацювання об’єкта. Період ІІ – це період нормальної експлуатації технічних об’єктів. Інтенсивність відмов в цей період практично не міняється (є незначне падіння). Це самий тривалий період експлуатації. В ІІІ – му періоді інтенсивність відмов зростає. Цей період називають періодом старіння та зносу.
Середнім напрацюванням до першої відмови Тсер називається математичне очікування часу напрацювання технічного об’єкта до першої відмови.
. (1.11)
Інтегруючи даний вираз по частинах, отримаємо
. (1.12)
Очевидно, що 
, оскільки при верхній межі Р(t) скоріше спрямовується до нуля, ніж t спрямовується до нескінченності. Таким чином,
. (1.13)
По даним випробувань Тсер однотипних об’єктів визначається
як:
(1.14)
де toi – час роботи i -го об’єкта до відмови;
N – загальне число об’єктів, поставлених на випробування.
Практично ж знати час тривалості справної роботи t0 всіх об'єктів, поставлених на випробування, не можливо.
Тому для обчислення Тсер користуються іншим виразом
(1.15)
де ∆ ni – число об’єктів, які відмовили в інтервалі часу ∆t
- середина і – го інтервала часу;
- число інтервалів;
tN – час, за який відмовили всі об’єкти, поставлені на випробування.
1.2.2 Безвідмовність обєктів, що підлягають ремонту.
Для об'єктів, які підлягають ремонту, характерне чередування справного стану і ремонту після відмови, тобто процес по експлуатації можна представити як послідовне чередування інтервалів часу працездатного і непрацездатного станів (рис.1.4).
Рис. 1.4 Чередування справного стану і ремонту об’єкта
Поява відмов в кожному з N об'єктів можна розглядати як потік вимог для ремонту.
Показниками безвідмовності ремонтованих об'єктів є:
– вірогідність безвідмовної роботи - Р(t);
– параметр потоку відмов - 
;
– середнє напрацювання на відмову.
Параметр потока відмов можна знайти за допомогою виразу:
. (1.16)
При цьому число об'єктів в процесі досліду залишається незмінним (об'єкти, що відмовили, замінюються новими).
Основним типом потоку відмов є простіший потік. Він, як відомо, задовольняє умовам ординарності, стаціонарності і відсутності післядії.
Якщо ремонтований об'єкт пропрацював сумарний час t∑ і мав за цей час n відмов, то середнє напрацювання на відмову у такого об'єкту рівне:
; (1.17)
Якщо потік відмов простіший, то параметр цього потоку і середнє напрацювання на відмову зв'язана між собою наступною залежністю:
. (1.18)
1.3 Основні закони розподілу часу безвідмовної роботи.
Внаслідок того, що час безвідмовної роботи є величина випадкова, для її опису в теорії надійності використовують ряд законів. Найбільшого поширення з них набули:
· розподіл Вейбулла;
· експоненціальний розподіл;
· розподіл Релея.
Розподіл Вейбулла має наступний вираз для вірогідності безвідмовної роботи:
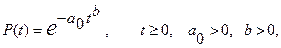(1.19)
де а0 - параметр масштаба;
b – параметр форми.
Звідси:
. (1.20)
Середній час безвідмовної роботи при цьому рівняється:
, (1.21)
де Г(1+1/b) – табульована повна гама-функція.
Інтенсивність відмов при розподілі Вейбулла рівняється:
. (1.22)
На рис. 1.5 показані основні залежності цього розподілу:
- для b< 1;
- для b> 1.
 |
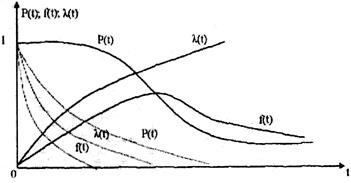Рис. 1.5 Основні залежності розподілу Вейбулла
Видно, що при b<1 інтенсивністьвідмов монотонно убуває, а при b>1 – монотонно зростає. Зазвичай значення b вибирається в межах від 1 до 2.
Закону Вейбулла досить добре підкоряється розподіл відмов в об'єктах, що містять велику кількість однотипних елементів, які не підлягають ремонту.
Експоненціальний розподіл можна розглядати як окремий випадок розподілу Вейбулла при b=1. Тоді
; 
; 
;
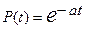. (1.23)
Звідси 
; або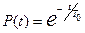 
.
При 
отримуємо: 
.
Залежності експоненціального розподілу представлені на рис.1.6.
 |
Рис. 1.6 Залежності експоненціального розподілу
При експоненціальному розподілі математичне очікування випадкової величини рівне средньоквадратичному відхиленню:
.
Експоненціальний розподіл типовий для більшості складних об'єктів, які містять велику кількість різних елементів, що не підлягають ремонту, коли відмови цих елементів переважно раптові.
Розподіл Релея також є окремим випадком розподілу Вейбулла при b =2. При цьому:
; 
; 
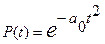. (1.24)
Введем новий параметр розподілу:
, тобто 
.
Тоді:
; 
; 
.
На рис.1.7 показані основні залежності при розподілі Релея.
 |
Рис.1.7 Основні залежності при розподілі Релея
Розподіл Релея досить добре описує поведінку ряду об'єктів і елементів з явно вираженим ефектом старіння і зносу.
1.4 Основні моделі надійності апаратури.
Моделлю надійності апаратури є графічне зображення основних елементів апаратури за їх функціональною ознакою. При цьому основні елементи і їх зв'язки виділяються так, щоб відмови будь-якого з них були незалежні і не зумовлювали відмов решти елементів. Простими універсальними моделями надійності апаратури є послідовні і паралельні схеми з'єднань з незалежних елементів.
Послідовна модель надійності - це система, що складається з двох і більш функціональних елементів, сполучених послідовно (рис.1.8). Тут Рі(t) – вірогідність безвідмовної работы і -го элемента.
 | |||||
 | |||||
 | |||||
Рис. 1.8 Послідовна модель надійності
Умовою працездатності такої моделі є: система залишається працездатною, якщо всі елементи моделі працездатні. При виході з ладу хоч би одного елементу система переходить в несправний стан.
На підставі теореми множення вірогідностей незалежних подій формулюється правило: вірогідність безвідмовної роботи послідовної моделі надійності рівна твору вірогідності безвідмовної роботи окремих її елементів.
, (1.25)
де Рс (t) – вірогідність безвідмовної роботи системи (моделі в цілому);
n – число послідовно включених елементів системи.
Вірогідність появи відмови в такій системі очевидно рівна:
. (1.26)
Якщо модель складається з однакових елементів з точки зору надійності, тобто 
, то:
(1.27)
Інтенсивність відмов послідовної моделі надійності очевидно рівна:
, (1.28)
де λі (t) - інтенсивність відмов і – го елемента системи.
Якщо елементи системи мають однакову надійність, тобто
, то
. (1.29)
Паралельна модель надійності відображає систему, що складається з двох і більше функціональних елементів, сполучених паралельно (рис. 1.9).
Умова працездатності моделі полягає в тому, що система залишається працездатною, якщо хоча б один з елементів знаходиться в справному стані. На підставі цієї властивості з використанням теореми множення вірогідностей незалежних подій формулюється правило: вірогідність відмови паралельної
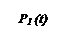
Рис.1.9 Паралельна модель надійності
моделі надійності рівна твору вірогідності відмови окремих її елементів. Тому:
. (1.30)
Тут Qc (t) – вірогідність відмови системи (моделі в цілому);
Qi (t) – вірогідність відмови і – го елемента системи;
Pi (t) = 1 – Qi (t) – вірогідність безвідмовної роботи і – го елемента системи.
Вірогідність безвідмовної роботи системи очевидно буде рівна:
. (1.31)
Якщо в системі всі елементи, що сполучені паралельно, мають одинакову надійність, тобто , то
(1.32)
1.5. Чинники, що впливають на показники надійності.
На надійність апаратури впливає ціла серія чинників. Їх умовно можна розбити на дві групи: суб'єктивні чинники і об'єктивні чинники.
До суб'єктивних чинників відносяться чинники в тій чи іншій мірі залежні від діяльності людини. Це, перш за все заходи, пов'язані з проектуванням і конструюванням апаратури, вибором матеріалів і елементів, забезпеченням режимів роботи, організацією техобслуговування.
До об'єктивних чинників відносяться чинники, пов'язані з кліматичними, метеорологічними, біологічними, механічними, космічними і ін. діями на апаратуру.
По характеру дії чинники, що впливають на надійність ділять на дві групи:
а) конструктивно-виробничі;
б) експлуатаційні.
До першої групи відносяться чинники, пов'язані з розробкою, проектуванням і виготовленням апаратури.
До експлуатаційних відносяться чинники, що впливають на надійність апаратури в процесі її експлуатації.
Розглянемо стисло деякі з конструктивно-виробничих і експлуатаційних чинників.
Серед конструктивно-виробничих чинників вагоме місце займають електричні режими роботи апаратури. Робота елементів при граничних електричних навантаженнях різко скорочує термін їх служби, знижує надійність апаратури. Зменшення електричних навантажень до оптимальних збільшує надійність апаратури.
Електричні режими роботи оцінюють по величині коефіцієнта навантаження по потужності або по напрузі:
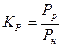, або 
.
Тут KP (KU) – коефіцієнт електричного навнтаження об’єкта по потужності (напрузі);
Рр (Up) – робоче електричне навантаження об’єкта по потужності (напрузі);
Pн (Uн ) – номінальне електричне навантаження об’єкта по потужності (напрузі);
При проектуванні апаратури зазвичай приймають коефіцієнт електричного навантаження 0,4–0,6.
Серед експлуатаційих чинників вагоме місце займають температура і вологість навколишнього середовища, забрудненість повітря і механічні навантаження.
Несприятливо діють на надійність як негативні так і позитивні значення температури. Так, наприклад, при збільшенні температури з +20 до +85оС інтенсивність відмов германієвих транзисторів збільшується в три рази, а у інтегральних мікросхем в 2-3 рази. Для експлуатації апаратури нормальною вважається температура +(25 ±10)о по Цельсію.
Вельми помітно на надійність апаратури впливає і вологість. Підвищена вологість приводить до погіршення електричних характеристик діелектриків зі всіма витікаючими з цього наслідками.
Інтенсивність відмов апаратури із збільшенням вологості збільшується згідно виразу:
λ в = λнв кв,
де λв - інтенсивність відмов апаратури з урахуванням підвищеної вологості;
λнв - інтенсивність відмов апаратури при нормальній вологості;
кв – поправочний коефіцієнт, який враховує вплив вологості на інтенсивність відмов апаратури.
Деякі значення кв приведені в таблиці 1.1.
Таблиця 1.1
| Вологість, % | Температура, оС | Значення коефіцієнта кв |
| 60-70 | 20-40 | |
| 90-98 | 20-25 | |
| 90-98 | 30-40 | 2,5 |
Нормальною вважається відносна вологість (60-65)%.
На надійність апаратури помітно впливає також забрудненість повітря як механічними, так і хімічними домішками.
Механічні навантаження (удари і вібрації) приводять до порушення цілісності паянь, контактів, обривам монтажних проводів і тому подібне. Механічну дію на надійність апаратури прийнято оцінювати за значенням створюваного прискорення.
Практика показує, що найбільш небезпечними є вібрації з частотами 10-150 Гц і 175-500 Гц.
Унаслідок вібрації і ударів параметр потоку відмов в апаратурі збільшується в 10-100 разів.
Для захисту апаратури від ударів і вібрацій застосовують різні амортизатори.
2 Методи підвищення надійності
2.1 Загальні методи підвищення надійності.
Високу надійність апаратури можна забезпечити ще на стадії її проектування і виробництва. Методами підвищення надійності апаратури на даній стадії є:
– правильний вибір схемних і конструктивних рішень;
– заміна аналогової обробки цифровою;
– правильний вибір елементів і матеріалів;
– заміна механічних перемикаючих і управляючих пристроїв електронними;
– правильний вибір електричних режимів роботи елементів і пристроїв апаратури;
– розробка мір по зручності технічного обслуговування і експлуатації апаратури;
– врахування вимог ергономіки;
– вибір відповідної технології виробництва апаратури і строге її дотримання;
– впровадження автоматизації при виробництві апаратури;
– вхідний контроль матеріалів і елементів;
– попереднє тренування елементів і апаратури;
– правильна методика настройки апаратури;
– поточний і вихідний контролі.
До підвищення надійності апаратури ведуть і заходи на стадії її експлуатації. Сюди входять заходи щодо зниження впливу об'єктивних чинників, що знижують надійність, і заходи щодо поліпшення організації процесу експлуатації апаратури. До поліпшення організації експлуатації апаратури ведуть наступні заходи:
– правильне планування профілактичних робіт;
– забезпечення експлуатації необхідною діагностичною і контрольно-вимірювальною апаратурою;
– правильний вибір кількості і номенклатури ЗІП;
– підвищення кваліфікації обслуговуючого персоналу.
2.2 Підвищення надійності шляхом впровадження мікроелектроніки.
Важливим заходом, який веде до підвищення надійності апаратури, є широке впровадження в неї мікроелектроніки.
Залежно від технології виготовлення інтегральні мікросхеми (ІМС) ділять на напівпровідникові, плівкові і гібридні.
Напівпровідникові ІМС є надійнішими і дешевшими зі всіх інтегральних структур. Досвід експлуатації і систематизація даних по відмовах напівпровідникових ІМС показав, що їх надійність визначається чотирма компонентами:
– зовнішніми з'єднаннями;
– внутрішніми контактними з'єднаннями;
– площею кристалів;
– корпусами ІМС.
При експоненціальному законі надійності інтенсивність відмов ІМС (λіс) можна представити як
λіс = λзз + λвкз + λкорп + λкр ,
де λзз – інтенсивність відмов зовнішніх з'єднань;
λвкз – інтенсивність відмов внутрішніх контактних з'єднань;
λкорп – інтенсивность відмов корпусів ІМС;
λкр – інтенсивность відмов кристала напівпровідника.
Надійність сучасних ІМС середньому ступеню інтеграції достатньо висока і оцінюється в даний час величиною
λіс = 10-8 1/ год.
Орієнтовні розрахунки показують, що середнє напрацювання на відмову при застосуванні ІМС в порівнянні з вариатом побудови апаратури на звичайних активних і пасивних елементах зростає в десятки тисяч разів.
Використання ІМС, крім того, дозволяє різко зменшити габарити, масу, споживану потужністю (у 10-100 разів і більш), вартість, підвищити швидкодію.
2.3. Підвищення надійності шляхом резервування апаратури.
Резервування апаратури - це один з ефективних способів підвищення надійності. Надійність апаратури при резервуванні може бути вище за надійність елементів, з яких складається апаратура. Разом з тим резервування веде до ускладнення апаратури, збільшення її вартості і споживаної нею енергії.
Розрізняють три методи резервування:
– загальне, що передбачає резервування об'єкта в цілому;
– роздільне, що передбачає резервування окремих елементів, їх груп або окремих вузлів;
– змішане, що передбачає поєднання загального і роздільного резервувань.
Відношення числа резервних елементів до резервованих називається кратністю резервування. Розрізняють однократне резервування (дублювання) і багатократне.
Крім того, резервування може бути з відновленням (з ремонтом тих елементів, що відмовили) і без відновлення. Сам резервний елемент може бути ремонтованим і таким, що не підлягає ремонту.
Існує три способи включення резерву: постійне, заміщенням і ковзаюче.
Постійним називають таке резервування, при якому резервні елементи беруть участь у функціонуванні об'єкту нарівні з основними. Природно, що резервні елементи знаходяться в такому режимі, що і основні, їх ресурс витрачається разом з резервованими елементами.
Недолік постійного резервування в тому, що апаратура значно збільшується в об'ємі і відмова резерву приводить до зміни параметрів і режиму роботи всього об'єкту.
Резервування, при якому функції основного елементу передаються резервному тільки після відмови основного елементу, називають резервуванням заміщенням. При цьому обов'язкова наявність комутуючих пристроїв для підключення резервних елементів замість тих, що відмовили.
Резервні елементи при цьому можуть знаходитися в різних режимах: навантаженому, полегшеному і ненавантаженому. Включення резервних елементів може здійснюватися уручну або автоматично.
Ковзаюче резервування застосовується за наявності в апаратурі однакових елементів (вузлів, блоків). При цьому один або декілька резервних елементів можуть заміщати будь-який з основних елементів даної групи, що відмовили. Для реалізації ковзаючого резервування необхідний логічний пристрій і комутатор.
2.4 Безвідмовність апаратури при загальному і роздільному резервуванні
Розглянемо вірогідність безвідмовної роботи апаратури при її загальному і роздільному постійному резервуванні.
а) Загальне постійне резервування.
Схема загального постійного резервування зображена на рис.2.1.
Рис. 2.1 Схема загального постійного резервування
Система із загальним постійним резервуванням нормально працюватиме при збереженні працездатності хоч би однієї з гілок.
На підставі теореми множення вірогідностей можна знайти вірогідність відмови такої системи - Qзп:
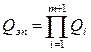, (i = 1,2,…,m+1), (2.1)
де Qi –вірогідність відмови і -ої гілки, що складається з n елементів.
У свою чергу безвідмовна робота і -ої гілки матиме місце при безвідмовній роботі кожного з n елементів. Тому:
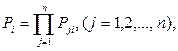(2.2)
де Рі - вірогідність безвідмовної роботи і -ої гілки;
Рji – вірогідність безвідмовної роботи j -го елемента і -ої гілки.
Вірогідність відмови і – ої гілки запишемо у вигляді:
. (2.3)
Вірогідність безвідмовної роботи системи тоді буде рівна:
. (2.4)
Якщо всі елементи однакові по надійності, тобто 
, то
. (2.5)
При експоненціальному законі надійності, коли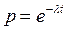 
отримаємо:
. (2.6)
Тут λ0 = n λ – інтенсивність відмов одної гілки системи.
Знайдем середній час роботи системи до відмови при умові рівнонадійності всіх елементів:
(2.7)
Тут Т0 - середній час безвідмовної роботи одної гілки системи;
Аm - коефіцієнт, який залежить від кратності резервування:
.
Нижче приведені значення Аm для різних кратностей резервування – m:
m 1 2 3 4 5
Аm 1,5 1,83 2,08 2,28 2,45
Видно, що при однократному резервуванню (дублюванню) середній час безвідмовної роботи системи Тзп збільшується в півтора рази в порівнянні з середнім часом безвідмовної роботи об’єкта без резервування Т0 (ланки). При трьохкратному резервуванню таке збільшення досягає 2.08.
б) Роздільне постійне резервування.
Схема роздільного постійного резервування зображена на рис.2.2. В ній послідовно сполучені n гілок, в кожній з яких паралельно сполучені (m+1) однотипних елементів.
Рис.2.2 Схема роздільного постійного резервування
Вірогідність відмови j – ої гілки - Qj очевидно рівна:
, (2.8)
де Qjі - вірогідність відмови і – го елемента в j – ій гілці;
Рjі - вірогідність безвідмовної роботи і – го елемента в j – ій гілці.
Оскільки всі елементи в гілці однотипні (а значить рівнонадійні), то
, (2.9)
де pj – вірогідність безвідмовної роботи одного елемента в j – ій гілці.
Вірогідність безвідмовної роботи j – ої гілки - Рj очевидно рівна:
. (2.10)
Вірогідність безвідмовної роботи системи в цілому - Ррп знаходиться як:
. (2.11)
Якщо всі гілки однотипні, то:
, (2.12)
де р – вірогідність безвідмовної роботи одного елемента системи.
Аналіз показує, що роздільне резервування ефективніше, ніж загальне. Дійсно, для відмови системи з загальним резервуванням досить, щоб в кожній гілці відмовив хоч би один елемент. Для відмови ж системи з роздільним резервуванням необхідно, щоб услід за відмовою якого-небудь робочого елементу відмовили всі елементи, що його резервують. Вірогідність такої події менша, ніж попередньої.
3 Розрахунок надійності апаратури
3.1 Аналітичний розрахунок надійності.
Під розрахунком надійності розуміють визначення числових значень показників безвідмовності за тими або іншими початковими даними. Розрізняють аналітичні методи розрахунку надійності і розрахунок надійності за статистичними даними, отриманими в процесі експлуатації апаратури або при її випробуванні. Аналітичні методи розрахунку надійності використовуються при проектуванні апаратури.
Апаратура, як відомо, складається з окремих блоків, вузлів, елементів. Від їх надійності залежить реалізація заданих параметрів надійності апаратури в цілому. Отже, необхідно розподілити вимоги по надійності апаратури в цілому по окремих її частинах.
Вважається, що з погляду надійності підсистеми в системі включені послідовно. Тому вірогідність безвідмовної роботи апаратури в цілому (системи) за час t буде рівна:
, (3.1)
де Рі (t) – вірогідність безвідмовної роботи і – ої підситеми;
N – число підсистем в системі.
При експоненціальному розподілі часу безвідмовної роботи
, (3.2)
де λі – інтенсивність відмов і – ої підситеми.
Для системи має
, (3.3)
де 
- інтенсивність відмов системи в цілому.
Якщо і -та підсистема складається з К груп елементів і в кожній групі nij елементів, то:
, (3.4)
де λіj - інтенсивність відмов j – ої групи однотипних елементів в
і – тій підсистемі.
Для системи в цілому:
. (3.5)
Нижче в таблиці приведені усереднені дані про інтенсивність відмов ряду елементів радіоелектронної апаратури.
Таблиця 3.1
| Найменування елементів | Інтенсивність відмов
 * 10-6,г-1
|
| ЕВП | 1.0-35.0 |
| Резістори | 0.01-1 |
| Конденсатори | 0.1-16.0 |
| Трансформатори | 0.02-6.5 |
| Дроселі, котушки індуктивності | 0.02-4.4 |
| Реле | 0.5-100 |
| Напівпровідникові діоди | 0.12-50 |
| Напівпровідникові тріоди | 0.003-3.0 |
| Комутаційні пристрої | 0.01-9.0 |
| Штепсельні роз'єми (на 1 штирок) | 1.11-0.025 |
| З'єднання паянням | 0.1-1.0 |
| ІМС | 0.001-0.01 |
На практиці дуже часто доводиться обчислювати вірогідність безвідмовної роботи високонадійних систем. При цьому твір
навіть при великих значеннях t виходить значно менше одиниці. В цьому випадку можна користуватися наближеним обчисленням P(t):
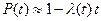. (3.6)
Обчислення кількісних характеристик надійності по наближених формулах не дає великих помилок для систем, вірогідність безвідмовної роботи яких перевищує 0,9.
При розрахунку надійності систем часто доводиться перемножувати вірогідності безвідмовної роботи, підносити їх до ступеня і витягувати з них корні. При значеннях P(t) близьких до одиниці ці обчислення можна з достатньою точністю виконувати по наступних наближених формулах:
;
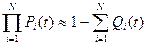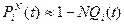; (3.7)
.
Тут Qi(t) = 1 - Рi(t) – вірогідність відмови і -го об’єкта.
3.2 Види аналітичного розрахунку надійності.
Залежно від повноти враховування чинників, що впливають на надійність, розрізняють прикидочний, орієнтовний і остаточний розрахунок надійності.
3.2.1 Прикидочний розрахунок надійності.
При проведенні прикидочного розрахунку надійності вважається, що:
- всі елементи виробу рівнонадійні;
- інтенсивності відмов всіх елементів виробу не залежать від часу (
);
- відмова будь-якого елементу приводить до відмови всього виробу (тобто елементи включені послідовно з точки зору надійності).
Прикидочний розрахунок надійності застосовується в наступних випадках:
- при перевірці вимог по надійності, висунутих замовником в технічному завданні (ТЗ) на проектування виробу;
- при розрахунку нормативних даних по надійності на окремі блоки, пристрої системи;
- для визначення мінімально допустимого рівня надійності елементів проектованого виробу;
- при порівняльній оцінці надійності окремих варіантів виробу на етапах передескізного і ескізного проектування.
Прикидочний розрахунок надійності дозволяє судити про принципову можливість забезпечення необхідної надійності виробу.
3.2.2 Орієнтовний розрахунок надійності
При орієнтовному розрахунку надійності враховується вплив на надійність тільки кількості і номенклатури використаних в апаратурі елементів.
Орієнтовний розрахунок надійності грунтується на наступних припущеннях:
- всі елементи даного типу рівнонадійні;
- всі елементи працюють в номінальних умовах і режимах;
- інтенсивності відмов всіх елементів не залежать від часу, тобто ().
Для виконання орієнтовного розрахунку надійності необхідно знати:
- вид з'єднання елементів з точки зору надійності;
- типи елементів, що входять у виріб, і число елементів кожного типу;
- величини інтенсивностей відмов елементів кожного типу.
Орієнтовний розрахунок надійності виконується після розробки принципових електричних схем виробу. Він дозволяє визначити раціональний склад елементів виробу і намітити шляхи підвищення надійності цього виробу.
Значення інтенсивностей відмов елементів кожного типу беруться з відповідних таблиць, які наведені в спеціальній літературі, і довідниках по розрахунку надійності.
3.2.3 Остаточний розрахунок надійності
Інтенсивності відмов елементів апаратури, як відомо, залежить від ряду впливаючих чинників. Найбільш істотними з них є: навколишня температура і швидкість її зміни; відносна вологість повітря; електричне навантаження; механічні навантаження (удари, вібрації, прискорення).
При експлуатації апаратури в реальних умовах інтенсивність відмов елементів знаходять як твір:
, (3.8)
де 
- інтенсивність відмов і – го об’єкта з урахуванням впливу на його надійність ряду чинників;
- інтенсивність відмов і – го об’єкта в номінальних умовах його експлуатації;
– поправочний коефіцієнт, що враховує вплив на надійність і – го об’єкта j - го чинника;
n – число чинників, вплив на надійність яких враховується.
Остаточний розрахунок надійності виробу можна виконувати тоді, коли відомі режими роботи елементів у виробі і умови експлуатації виробу. Для виконання остаточного розрахунку надійності необхідно знати:
· режими роботи елементів кожного типу;
· поправочні коефіцієнти для основних, впливаючих на надійність чинників.
Якщо розрахункові показники надійності не задовольняють заданим, то необхідно приймати заходи по підвищенню надійності спроектованої апаратури.
3.3 Розрахунок надійності за статистичними даними.
Для оцінки надійності за статистичними даними необхідна велика робота по правильному і об'єктивному збору цих даних.
Розрахунок надійності за статистичними даними може проводитися або в процесі випробувань на надійність, або на основі досвіду експлуатації апаратури. Для збору статистичних даних про надійність розробляються спеціальні документи, в які заносяться всі необхідні дані для розрахунку надійності. Основними документами є журнал обліку відмов і звіти про надійність.
При розрахунку надійності за даними звітів для кожного типу апаратури складається таблиця потоку відмов (табл.3.2).
Таблиця 3.2
| Номер відмови | ||||||||||||
| Напрацю- вання (год.) | ||||||||||||
| Номер відмови | ||||||||||||
| Напрацю- вання (год.) | ||||||||||||
| Номер відмови | ||||||||||||
| Напрацю- вання (год.) |
На підставі цієї таблиці будується варіаційний ряд напрацювання даного пристрою (табл. 3.3):
Таблиця 3.3
| Номер відмови | ||||||||||||
| Напрацю- вання (год.) | ||||||||||||
| Номер відмови | ||||||||||||
| Напрацю- вання (год.) | ||||||||||||
| Номер відмови | ||||||||||||
| Напрацю- вання (год.) |
При великому числі спостережень (порядка декілька сотень) варіаційний ряд стає громіздким і малонаочним. Для додання йому компактності проводять додаткову обробку ряду. Для цього весь діапазон зафіксованих значень відмов ділиться на інтервали часу tі і підраховується кількість відмов Δ ni в кожному і - му інтервалі.
Далі будується таблиця (табл.3.4) в якій приводяться інтервали в порядку їх розташування уздовж осі абсцис, число відмов в кожному інтервалі, оцінки показників надійності, розрахованих для кожного інтервалу.
Таблиця 3.4
| tі
| Δ nі | Pi | Qi | fi | i
| Тi (год.) |
Ця таблиця називається статистичним рядом. За даними цього ряду будуються гістограми для оцінюваних показників надійності. Статистичний ряд за даними таблиці 3.3. має вигляд (табл.3.5).
Таблиця 3.5
| tі
| Δ nі | Pi | Qi | fi (1/год.) | i (1/год.)
| Тi (год.) |
| 0 – 20 | 0.47 | 0.54 | 0.027 | 0.036 | 27.8 | |
| 20 – 40 | 0.3 | 0.7 | 0.0083 | 0.022 | 45.5 | |
| 40 – 60 | 0.23 | 0.77 | 0.0033 | 0.0125 | ||
| 60 – 80 | 0.13 | 0.87 | 0.005 | 0.027 | ||
| 80 – 100 | 0.07 | 0.93 | 0.0033 | 0.033 | 30.3 | |
| 100 - 120 | - | - | - | - |
Гістограми, які побудовані по даним таблиці 3.5, представлені на рисунках 3.1 і 3.2
Рис. 3.1 Гістограма для вірогідності безвідмовної роботи
Рис.3.2 Гістограма для інтенсивності відмов
Побудовані гістограми апроксимуються кривими, по вигляду яких можна приблизно встановити закони зміни показників надійності в часі шляхом порівняння з відповідними теоретичними кривими.
4 Розрахунок запасних частин
4.1 Призначення і типи запасних частин.
Для проведення робіт по технічному обслуговуванню і ремонту необхідно мати запасні частини і матеріали. У зв'язку з цим підприємства-виробники разом з приладами поставляють і комплекти запасних частин, інструментів і приладдя (ЗІП). Досвід експлуатації складних систем свідчить про те, що час відновлення працездатності устаткування після відмови істотним чином залежить від наявності запасних елементів. Так, при експлуатації систем високої готовності до дії відсутність ЗІП збільшує час відновлення в 10-20 разів.
Аналіз складу і витрати запасних елементів в складних системах показує, що по окремих типах елементів запас перевершує потреби, тоді як в деяких інших елементах відчувається його недолік. З цього виходить, що впровадження в практику науково обгрунтованих методів розрахунку кількісного складу ЗІП до дорогого устаткування приведе до підвищення характеристик відновлюваності останнього і отриманню істотного економічного ефекту. Практичне значення має знаходження кількісних співвідношень між числом запасних елементів і вірогідністю того, що на заданому інтервалі часу роботи дана система не простоюватиме через відсутність необхідних запасних елементів, надійністю елементів і вартістю ЗІП. В даний час вартість ЗІП складає 20% і більш від загальної вартості устаткування. Зміст запасних елементів зв'язаний з великими економічними витратами; при цьому може опинитися, що значне збільшення вартості ЗІП не дасть істотного ефекту в зменшенні часу простою, тобто фактичні витрати не виправдають отриманого виграшу.
Комплект запасних частин повинен містити всі необхідні в процесі експлуатації устаткування елементи.
Залежно від призначення і особливостей використання комплекти ЗІП розділяють на одиночні, групові і ремонтні.
Одиночний комплект ЗІП служить для підтримки працездатності об'єкту протягом встановленого часу, рівного ресурсу об'єкту (або терміну служби), з вірогідністю безвідмовної роботи не нижче заданої при мінімальних витратах часу і засобів. Одиночний комплект ЗІП входить в об'єм постачання, його вартість - у вартість виробу.
Груповий комплект ЗІП вибирається для групи однотипного устаткування і зберігається на складах або на базі, призначений для проведення аварійного ремонту устаткування агрегатним методом, поповнення одиночних комплектів, а також для забезпечення приладу такими елементами,
