В булевых алгебрах существуют двойственные утверждения, которые либо одновременно верны, либо одновременно неверны. Именно, если в формуле, которая верна в некоторой булевой алгебре, поменять все конъюнкции на дизъюнкции, 0 на 1, ≤ на ≥ и наоборот, то получится формула также истинная в этой булевой алгебре. Это следует из симметричности аксиом относительно таких замен.
Пусть 
― произвольная формула булевой алгебры, содержащая булевы переменные 
.
Формула
называется двойственной формуле .
Для двойственныхформул справедлив принцип двойственности. Если
то и обязательно
а также, если
то и обязательно
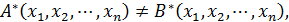
Так как любая формула булевой алгебры определяет булеву функцию, то понятие двойственности можно использовать и для функций.
Булева функция 
называется двойственной функции 
, если
.
Отношение двойственности булевых функций симметричное
.
Булева функция, для которой 
называется самодвойственной.
Построим таблицу истинности для функци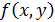и 
и 
учитывая, что 
, 
и т. д.
.
С этой таблицы можно сформулировать правило построения таблицы истинности двойственной функции.
Для построения таблицы истинности двойственной функции, необходимо:
1. построить таблицу истинности заданной функции;
2. каждое ее значения инвертировать 
;
3. полученную строку записать в обратном порядке.
/*Пример 12.1
Известно, что булева функция 
на словах 001, 011, 111 (на первом, третьим и седьмом слове). Найти двойственную функцию 
.
Выполнение. Выпишем таблицу истинности функции, инвертируем ее значения на всех словах и полученную последовательность запишем в обратном порядке:
*/
Таблица истинности для самодвойственной функции двух переменных имеет вид
.
Как видно с этой таблицы, каждое значения самодвойственной функции равно значению симметричного к нему значения (симметричность относительно прямой, делящей таблицу истинности пополам). Таким образом, по таблице истинности всегда можно определить, самодвойственная ли функция, или нет.
/*Пример 12.2
Функци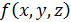и 
и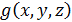 
заданы таблицами истинности.
.
Определить, самодвойственные ли данные функции.
Выполнение. С таблицы истинности видно, что каждое значение функции 
― отрицание симметричного значения:
, 
,
, 
.
Отсюда вывод: функция 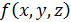― самодвойственная функция.
Функция 
не самодвойственная, так как
, 
. * /
Значения самодвойственной функции определяются полностью ее значениями на половине слов. Всего есть 
слов, половина от них равна 
. Таким образом, количество самодвойственных функций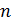 
переменных равно 
.
Пусть функция задана суперпозицией
.
Можно доказать, что для функции 
двойственная функция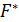 
имеет вид
.
Найдем двойственные функции до отрицания, конъюнкции, дизъюнкции, константы 0 и константы 1.
1. 
, 
.
2. 
, 
.
3. 
, 
.
4. 
, 
.
5. 
, 
.
Таким образом:
1. конъюнкция двойственная дизъюнкции, и наоборот;
2. константа 0 двойственная константе 1, и наоборот;
3. отрицание самодвойственная функция.
Отсюда следует правило построения двойственной функции:
Для того, чтобы получить двойственную функцию заданной булевой функции, представленной формулой булевой алгебры, необходимо заменить дизъюнкции на конъюнкции, и, наоборот, 0 на 1, и, наоборот, и использовать круглые скобки для сохранения первичного порядка выполнение операций.
/*Пример 12.3
Построить двойственную функцию функции
.
Выполнение. В формуле выполним необходимые замены:
.
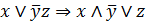Операция дизъюнкции в полученной формуле должна выполняться раньше, чем операция конъюнкции, поэтому используем скобки.
.
В результате получим двойственную функцию
. * /
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 9
Упражнение 1. Определить двойственную функцию функции 
по ее известному номеру 
и ее номер 
.
Выполнение. 
.
.
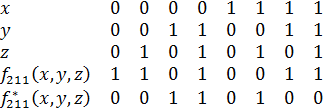Номер двойственной функции 
.
ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
| Вариант. |  
|
| 1. | 147. |
| 2. | 188. |
| 3. | 158. |
| 4. | 173. |
| 5. | 112. |
| 6. | 138. |
| 7. | 150. |
| 8. | 125. |
| 9. | 124. |
| 10. | 149. |
| 11. | 137. |
| 12. | 123. |
| 13. | 175. |
| 14. | 157. |
| 15. | 187. |
| 16. | 136. |
| 17. | 201. |
| 18. | 189. |
| 19. | 151. |
| 20. | 127. |
| 21. | 133. |
| 22. | 129. |
| 23. | 159. |
| 24. | 167. |
| 25. | 169. |
13. ПОЛИНОМ ЖЕГАЛКИНА, ЛИНЕЙНЫЕ ФУНКЦИИ
Полиномом Жегалкина называется конечная сумма по модулю 2 попарно различных элементарных конъюнкций. Количество переменных, входящих в элементарную конъюнкцию, называют рангом элементарной конъюнкции. Количество попарно разных элементарных конъюнкций полинома Жегалкина называют длиной полинома.
Любая булева функция 
может быть представленным единственным полиномом Жегалкина.
Алгоритм построения полинома Жегалкина булевой функции, заданной формулой алгебры Жегалкина:
1. Раскрыть скобки в заданной формуле. Для этого использовать дистрибутивностью конъюнкции относительно суммы по модулю 2
2. Упростить выражение, используя формулы (7.1 – 7.4).
/*Пример 13.1
Записать полином Жегалкина для импликации (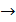
).
Выполнение.
. */
/*Пример 13.2
Записать полином Жегалкина для эквивалентности (~).
Выполнение.
. * /
Булева функция называется линейной, если она может быть представлена полином Жегалкина, не содержащего конъюнкций переменных.
/*Пример 13.3
Отрицание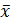 
―линейная функция, так как ее полиномЖегалкина 
не содержит конъюнкций переменных.
Дизъюнкция 
― не линейная функция, так как ее полином Жегалкина 
содержит конъюнкцию переменных х и у.
Импликация 
― не линейная функция, так как ее полином Жегалкина 
(Пример 13.1) содержит конъюнкциюпеременных х и у. Эквивалентность 
есть линейной функцией, так как ее полином Жегалкина 
(Пример 13.2) не содержит конъюнкций переменных. * /
/* Пример 13.4
Исследовать на линейность функцию
.
Выполнение. Построим полином Жегалкина:
.
Полином Жегалкина содержит конъюнкции переменных и поэтому функция
не линейная. * /
Для любой булевой функции существует только один полином Жегалкин а.
Для нахождения полинома Жегалкина можно использовать метод неопределенных коэффициентов. Суть этого метода понятна с примера.
/*Пример 13.5
Построить полином Жегалкина для импликации
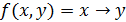
методом неопределенных коэффициентов.
Выполнение. Запишем полином для заданной функции в виде сложения по модулю 2 всех возможных элементарных конъюнкций переменных 
и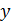 
з неопределенными коэффициентами:
, (*)
где коэффициенты 
принимают значения с множества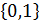 
и определяют присутствие или отсутствие элементарных конъюнкций в полиноме.
Вычислим значения функции на всех словах с использованием (*):
;
;
;
.
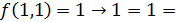
Поэтому
. */
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 10
Упражнение 1. Записать полином Жегалкина для булевой функции 
заданной формулой булевой алгебры.
Выполнение.
.
Окончательно:
.
Упражнение 2. Построить полином Жегалкина функции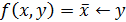 
методом неопределенных коэффициентов.
Выполнение.
.
,
.
.
.
.
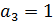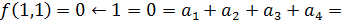
В результате:
.
ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
| Вариант | 
| 
|
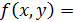
| 1. |  .
|  .
|
| 2. |  .
|  .
|
| 3. |  .
|  .
|
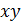| 4. |  .
|  .
|
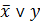| 5. |  .
|  .
|
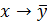| 6. |  .
|  .
|
| 7. |  .
|  .
|
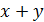| 8. |  .
|  .
|
| 9. |  .
|  .
|
| 10. |  .
|  .
|
| 11. |  .
|  .
|
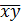| 12. |  .
| .
|
| 13. |  .
|  .
|
| 14. |  .
|  .
|
| 15. |  .
|  .
|
| 16. |  .
|  .
|
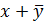| 17. |  .
| .
|
| 18. |  .
| .
|
| 19. |  .
|  .
|
| 20. |  .
|  .
|
| 21. |  .
| .
|
| 22. |  .
| .
|
| 23. |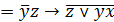 
| .
|
| 24. | 
|  .
|
| 25. | 
| .
|
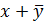14. ФУНКЦИИ, СОХРАНЯЮЩИЕ 0, ФУНКЦИИ, СОХРАНЯЮЩИЕ 1, МОНОТОННЫЕ ФУНКЦИИ
Булева функция 
называется функцией, сохраняющей 0, если на нулевом слове она принимает значение 0, то есть, если
.
Булева функция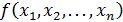 
называется функцией, сохраняющей 1, если на слове со всех единиц она принимает значения 1, то есть, если
.
/* Пример 14.1
Функци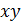и и сохраняют 0, так как
, 
Кроме этого, функции сохраняют 1, так как
, 
*/
/*Пример 14.2
Функция 
сохраняет 1 и не сохраняет 0, так как
,
*/
Введем на множестве слов отношение порядка, которое обозначим символом 
. Пусть 
и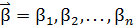 
― два слова. Тогда 
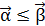, если 
, 
.
Если это не так, хотя бы для одной пари 
(
,), то слова 
и 
― несравнимы.
/*Пример 14.3
Для функций двух переменных:
, 
, 
, 
, 
,
, 
, 
, 
.
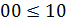Несравнимыми словами есть слова 01 и 10. * /
Булева функция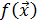 
называется монотонной, если для любых слов и , для которых ,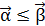 
,
, 
,
.
/*Пример 14.4
Исследовать на монотонность функцию
.
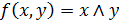Выполнение.
, 
;
, 
;
, 
;
, 
;
, 
.
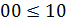Вывод: ― функция монотонная. * /
/* Пример 14.5
Исследовать на монотонность функцию
.
Выполнение.
.
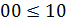
Вывод: функция ― не монотонная. * /
Булева функция, отличная от констант 0 и 1, монотонна, если и только если она допускает представления формулой булевой алгебры без отрицаний.
/*Пример 14.6
Определить, монотонная ли функция
.
Выполнение.
.
Полученная формула булевой алгебры не содержит отрицаний, поэтому 
― монотонная функция. * /
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 11
Исследовать на монотонность функцию
.
Выполнение.
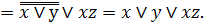
Таким образом
.
Полученная формула булевой алгебры не содержит отрицание, поэтому заданная функция монотонная.
ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
| Вариант |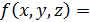
|
| 1. |  .
|
| 2. |  .
|
| 3. |  .
|
| 4. |  .
|
| 5. |  .
|
| 6. |  .
|
| 7. |  .
|
| 8. |  .
|
| 9. |  .
|
| 10. |  .
|
| 11. |  .
|
| 12. |  .
|
| 13. |  .
|
| 14. |  .
|
| 15. |  .
|
| 16. |  .
|
| 17. |  .
|
| 18. |  .
|
| 19. | .
|
| 20. | .
|
| 21. | .
|
| 22. |  .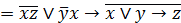
|
| 23. | .
|
| 24. | .
|
| 25. | .
|
15. КЛАССЫ ПОСТА. ТЕОРЕМА ПОСТА
Классами Поста называют следующие пять классов (множеств) булевых функций:
― класс функций, сохраняющих 0;
― класс функций, сохраняющих 1;
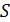― класс самодвойственных функций;
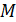― класс монотонных функций;
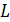― класс линейных функций;
Булева функция 
может принадлежать одному или нескольким классам Поста, а может и не принадлежать ни одному.
/*Пример 15.1
Булева функция 
принадлежит всем классам Поста.
Действительно:
― функция сохраняет 0;
― функция сохраняет 1;
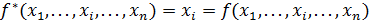― функция самодвойственная;
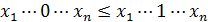и
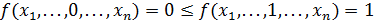― функция монотонная;
Функция не содержит конъюнкций, поэтому она линейная. * /
/*Пример 15.2
Функция 
(штрих Шеффера) не принадлежит ни одному классу Поста.
Действительно, 
имеет нелинейный полином Жегалкина и поэтому 
не принадлежит классу 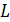линейных функций;
С таблицы истинности функции
следует, что
― функция не сохраняет 0;
― функция не сохраняет 1;
но 
― функция немонотонная;
, но 
― функция не самодвойственная. * /
Пусть 
― множество всех булевых функций, зависимых от любого числа переменных, и пусть 
― система булевых функций.
Замыканием множества называется множество 
, состоящее с булевых функций, которые можно получить суперпозицией функций с 
. Если 
, то множество булевых функций называется замкнутым классом
Система булевых функций называется функционально полной, если 
.
Каждый класс Поста замкнутый.
Система полная, если, и только если, она содержит хотя бы одну функцию, не сохраняющую 0, хотя б одну функцию, не сохраняющую 1, хотя б одну не самодвойственную функцию, хотя б одну не монотонную функцию и хотя б одну нелинейную функцию (теорема Поста).
Так как существуют булевы функции, которые не принадлежат ни одному классу Поста, то минимальное количество функций функционально полной системы булевых функций равно 1.
Полная система булевых функций называется несокращенной, если из нее нельзя исключить ни одной функции без потери свойства полноты. Отсюда, как следствие, следует, что максимальное количество функций несокращенной системы булевых функций равно четырем.
/* Пример 15.3
Определить по теореме Поста о полноте, есть ли система булевых функций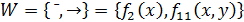 
функционально полной?
Выполнение. Функция 
не сохраняет ноль ( 
), не сохраняет единицу ( 
). Функция 
не самодвойственная. Это следует с таблицы истинности
Функция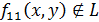 
не линейная. Действительно:
.
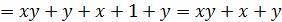Функция 
не монотонная. Действительно:
, но 
.
Все условия теоремы Поста выполняются, поэтому система функций 
― полная. */
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 12
Упражнение 1. Исследовать на принадлежность классам Поста булеву функцию
.
Выполнение. Преобразуем формулу, которой задана функция, в формулу булевой алгебры и формулу алгебры Жегалкина.
.
,
.
.
.
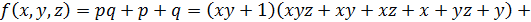
А теперь перейдем к исследованию принадлежности заданной функции классам Поста.
, функция не сохраняет 0, 
.
, функция не сохраняет 1, 
.
Функция нелинейная (
), так как ее полином Жегалкина 
содержит дизъюнкцию 
.
Функция немонотонная (
), так как ее формула булевой алгебры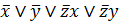 
содержит отрицание.
Так как двойственная функция
,
не равняется заданной функции, то последняя не самодвойственная,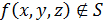 
.
ВАРИАНТЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
| Вариант |
|
| 1. |  .
|
| 2. |  .
|
| 3. |  .
|
| 4. |  .
|
| 5. |  .
|
| 6. |  .
|
| 7. |  .
|
| 8. |  .
|
| 9. |  .
|
| 10. |  .
|
| 11. |  .
|
| 12. |  .
|
| 13. |  .
|
| 14. |  .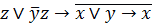
|
| 15. |  .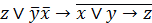
|
| 16. |  .
|
| 17. |  .
|
| 18. |  .
|
| 19. |  .
|
| 20. |  .
|
| 21. |  .
|
| 22. |  .
|
| 23. |  .
|
| 24. |  .
|
| 25. |  .
|
ЛИТЕРАТУРА
1. Игошин В.И. Математическая логика: учеб. пособие для студентов вузов / В.И. Игошин. ― М.: ИНФРАМ, 2012. ― 399 с.
2. Гринченков Д.В. Математическая логика и теория алгоритмов для программистов: учеб. пособие для студентов вузов / Д.В. Гринченков, С.И. Потоцкий. ― М.: КНОРУС, 2013. – 206 с.
3. Бондаренко М.Ф. Комп’ютерна дискретна математика: Підручник / М.Ф. Бондаренко, Н. В. Білоус, А. Г Руткас. ― Харків: «Компанія СМІТ», 2004. ― 480 с.
Михаил Васильевич Остапович
Павлина Васильевна Хмара
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ РАБОТ ПРИ ИЗУЧЕНИИ ДИСЦИПЛИНЫ «ТЕОРИЯ АЛГОРИТМОВ»
(Модуль 1 «БУЛЕВА АЛГЕБРА, АЛГЕБРЫ ЛОГИКИ И ЖЕГАЛКИНА»)
| Подписано в печать 1.07.2016. Формат 84х108/32. Бумага тип №1. Гарнитура Таймс. Печать офсетная. Уч.–изд. л. 4,0. Тираж 100 экз. |
Отпечатано в типографии
Гуманитарно-педагогической академии (г. Ялта)
РИО ГПА ул. Севастопольская, 2 а, г. Ялта
