Описание устройства и работы автоматической системы, разработка ее функциональной схемы.
Разработка математической модели и структурной схемы заданной системы.
Система «золотник — исполнительный механизм»
Гидравлическая система, состоящая из золотника и поршневого исполнительного механизма, может быть использована в качестве примера для рассмотрения методики вывода точных дифференциальных уравнений или передаточных функций. Система, показанная на рис. 2.1, состоит из четырехходового золотника, исполнительного механизма с поршнем и инерционной нагрузки. К центральному буртику золотника от внешнего источника подастся рабочая жидкость под постоянным давлением.
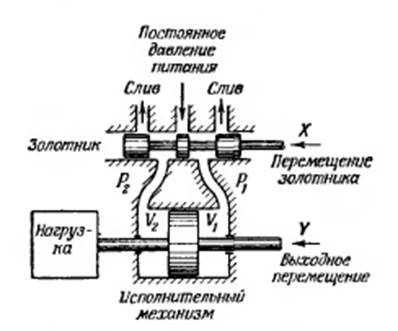
Рис.2.1. Гидравлическая система, состоящая из четырехходового золотника и исполнительного механизма.
Если золотник стоит в средней позиции, то рабочая жидкость не поступает к исполнительному механизму и, следовательно, скорость поршня и нагрузки будет равна нулю. Когда же золотник смещен в одном из направлений, поршень и нагрузка будут двигаться со скоростью, пропорциональной величине перемещения золотника. При смещении золотника в противоположном направлении от средней позиции жидкость будет поступать в другую полость силового цилиндра и произойдет реверс движения нагрузки. Перепад давлений на поршне исполнительного механизма, возникающий при смещении золотника со средней позиции, создаст силу, необходимую для движения нагрузки. Уравнение системы, помимо инерционной нагрузки, будет также учитывать вязкое трение на поршне, сжимаемость жидкости и утечки через золотник. Вывод основан на определении перемещений золотника, необходимых для обеспечения различных видов движения нагрузки: 1) для создания движения нагрузки с требуемой скоростью; 2) для обеспечения ускоренною движения нагрузки; 3) для обеспечения заданной степени изменении ускорения нагрузки и создания расхода, идущего на компенсацию сжимаемости жидкости. Для вывода используются следующие обозначения: X – перемещение золотника, см; Y – перемещения поршня и нагрузки, см; X1 – перемещение золотника, необходимое для создания скорости, см; Х2 перемещение золотника, необходимое для обеспечения ускоренного движения нагрузки, см; Х3 – перемещение золотника, необходимое для создания расхода, идущего на компенсацию сжимаемости жидкости, см; C1 коэффициент усиления по скорости, (см/сек)/см; α – коэффициент вязкого трения нагрузки и поршня, кг/(см/сек); KQ0 – коэффициент усиления по расходу при нулевом перепаде давлений па поршне, (см3/сек)/см; С2 – коэффициент усиления по усилию, кг/см, s = d/dt комплексный оператор; М – масса нагрузки и поршня, кг·сек2/см; А–площадь поршня, см2; V – эффективный объем жидкости, находящейся в системе, см3 (V составляет половину общего объема жидкости, заключенной между золотником и поршнем); Vi – объем жидкости, находящейся с одной стороны поршня, см3, V1 – объем жидкости, находящейся с другой стороны поршня, см3; Кр – коэффициент усиления по давлению, (кг/см2)/см; Р1 – изменение давления с одной стороны поршня, кг/см2; Р2 – изменение давления с другой стороны поршня, кг/см2; H – перепад давлений на поршне, кг/см2; В – объемный модуль упругости жидкости, кг/см2; ωр – резонансная частота, рад/с; δ – коэффициент демпфирования (безразмерная величина).
При данном перемещении золотника поршень и нагрузка будут двигаться с определенной скоростью. Это соотношение можно записать следующим образом:
| (2.1) |
 ,
,
 ,
,
Коэффициент усиления по скорости С1 получается из коэффициента KQ0, так как при наличии только инерционной нагрузки максимум скорости обычно возникает при нулевом перепаде давлений па поршне:

| (2.1) |
 .
.
Однако в выражении не учтено дополнительное перемещение золотника, требующееся для преодоления вязкого трения поршня и нагрузки α. Чтобы учесть вязкое трение, нужно использовать коэффициент усиления по усилию С2.
Таким образом, выражение для перемещения золотника, которое требуется для создания заданной скорости движения нагрузки, имеет вид
 .
.
Коэффициент усиления по усилию можно выразить через коэффициент усиления по давлению Kр:

| (2.1) |
 .
.
Сила, необходимая для создания ускорения инерционной нагрузки, определяется по второму закону Ньютона:
 .
.
С другой стороны, эту силу можно выразить через перемещение золотника и коэффициент усиления по усилию
 ,
,
 .
.
Для изменения ускорения нагрузки должна быть изменена скорость возрастания или убывания по времени давлений в полостях силового цилиндра. Так как жидкость сжимаема, то для того, чтобы изменить давление в полости, через золотник нужно пропустить расход, компенсирующий сжимаемость. Величина этого расхода зависит от объема жидкости в полости и от объемного модуля упругости. Для одной полости можно записать
 .
.
Считая, что золотник симметричен, для второй полости имеем
 .
.
Если допустить, что изменение перепада давлений на поршне равно сумме изменений давлений в полостях, то можно написать

Коэффициент  , выразим через коэффициент усиления по скорости C1
, выразим через коэффициент усиления по скорости C1

Перепад давлений на поршне H можно выразить через силу, необходимую для создания ускорения инерционной нагрузки, и силу, идущую на преодоление вязкого трения

Объединяя уравнения и, получим

Полное перемещение золотника, обеспечивающее все заданные случаи движения нагрузки, получается при суммировании уравнений, и, т. е.
 .
.
Следовательно,
 .
.
Передаточная функция, полученная из уравнения, будет иметь вид

Наличие колебательного звена в передаточной функции означает, что гидравлическая система «золотник — исполнительный механизм» является системой резонансного типа, подобно механической системе «пружина—масса». Следовательно, для такой системы можно записать выражения для резонансной частоты и коэффициента демпфирования

| (2.1) |
 ,
,

| (2.1) |
 .
.
Передаточную функцию с учетом уравнений и можно представить как

| (2.1) |

Коэффициенты уравнения или передаточной функции сервомеханизма «золотник – исполнительный механизм» можно вычислить, используя постоянные коэффициенты системы. Сила вязкого трения и коэффициенты усиления золотника по расходу и давлению могут быть замерены, если для данной системы эти величины не известны. Характеристики золотника обычно нелинейны. Однако указанные коэффициенты золотника можно линеаризировать, считая, что границы рабочего диапазона не должны приближаться к точкам насыщения.
Коэффициент усиления по давлению Кр определяет величину изменения давления в полости силового цилиндра на единицу перемещения золотника. Использование методики, для определения коэффициентов усиления золотника по расходу и давлению, обусловливает получение линеаризированной передаточной функции системы «золотник– исполнительный механизм». Следует заметить, что хотя в рассматриваемом сервомеханизме величина вязкого демпфирования и превышает демпфирование, обусловленное утечками, его влияние на резонансную частоту системы весьма незначительно.
Когда поршень находится в крайних положениях, резонансная частота возрастает незначительно, и этим изменением обычно пренебрегают.
Система «насос – гидродвигатель»
Сервомеханизм «насос – гидродвигатель» предназначается для управления вращательным движением нагрузки. Этот сервомеханизм можно также назвать усилителем мощности, так как он обеспечивает большую мощность на выходном валу. Если устройство «золотник — поршневой исполнительный механизм» имеет довольно ограниченную номинальную мощность, то мощность на выходе гидродвигателя можно изменять от десятых долей до нескольких сотен лошадиных сил.
При анализе этого типа привода будут рассмотрены насос и двигатель с радиальным расположением поршней.
Методику анализа можно также без изменений применять к аксиально-поршневым или лопастным гидроагрегатам, так как их основные принципы действия идентичны. Рассматриваемый сервомеханизм схематично показан на рис.4.2.

Рис.4.2 – Гидравлический сервомеханизм «насос - гидродвигатель»
Сервомеханизм состоит из насоса с переменной производительностью, приводящегося во вращение электродвигателем с постоянной скоростью, и из гидродвигателя, который соединяется с нагрузкой через шестеренчатую передачу. Направление и величина расхода на выходе насоса регулируются в данном случае изменением эксцентриситета между центром внешней обоймы и центром блока, в котором находятся плунжеры. Посредством гидродвигателя расход и давление преобразуются в скорость вращения и момент на выходном валу, который жестко соединен с нагрузкой.
Гидросистема, соединяющая насос с гидродвигателем, представляет собой замкнутый объем, и поэтому утечки жидкости должны восполняться через обратные клапаны посредством гидроаккумулятора или насоса подпитки. По этой причине давление в сливной магистрали для этого типа гидроприводов должно быть равно давлению подпитки. В противоположность разности давлений в полостях силового цилиндра, управляемого четырех ходовым золотником, в данном типе привода давление изменяется только в одной из магистралей между насосом и двигателем, а в другой остается равным давлению подпитки. Рабочее давление в приводе является функцией сопротивления нагрузки. Уравнение привода и передаточная функция, определяющая отношение угла поворота выходного вала двигателя к величине эксцентриситета насоса, выводятся с учетом только инерционной нагрузки. Принимаются во внимание также вязкое трение и потери момента в гидродвигателе, включая эффекты от сжимаемости жидкости и демпфирования, вызванного утечками.
При выводе будут использованы следующие обозначения: S — величина эксцентриситета насоса, см; θд – угол поворота выходного вала гидродвигателя, рад; θн – угол поворота нагрузки, рад; dд - удельный объем гидродвигателя, см3/рад; dн - максимальная удельная производительность насоса, см3/рад; Jн – момент инерции нагрузки, кг·см·с2; Jд – момент инерции гидродвигателя, кг·см·с2; Kg – передаточное отношение θн/θд; J – общий момент инерции, приведенный к валу гидродвигателя, кг·см·с2; Кутд – коэффициент утечек в гидродвигателе, (см3/сек)/(кг/см2); Кутн – коэффициент утечек в насосе, (см3/сек)/(кг/см2); KQ — коэффициент усиления насоса по расходу, (см3/сек)/(кг/см2); Кр—коэффициент усиления насоса по давлению (кг/см2)/см; V – эффективный объем жидкости в гидросистеме, см3 (равен половине общего объема жидкости между насосом и гидродвигателем; s = комплексный оператор; ωр – резонансная частота, рад/с; В – объемный модуль упругости жидкости, кг/см2; δ — коэффициент демпфирования; H – разность давлений в напорной и сливной магистралях гидродвигателя, кг/см2; а коэффициент вязкого трения гидродвигателя и нагрузки, кг·см/(рад/с); Ка – коэффициент усиления привода по скорости, (рад/сек)/см; Км – коэффициент усиления привода по моменту (кг·см/рад)/см; N – скорость вращения насоса, рад/с; Smax – максимальная величина эксцентриситета насоса, см; Sск – величина эксцентриситета, идущая на создание скорости движения нагрузки, см; Sут – величина эксцентриситета, необходимая дли создания расхода, компенсирующего утечки рабочей жидкости, см; Sсж – величина эксцентриситета необходимая для создания расхода, компенсирующего сжимаемость жидкости, см.
Анализ привода «насос — гидродвигатель» заключается в определении значений эксцентриситета насоса, требующихся для обеспечения различных видов движения нагрузки. Уравнение и передаточные функции выводятся для случая движения нагрузки с постоянной скоростью, а также для случаев движения нагрузки с постоянным и переменным ускорением, когда необходимо компенсировать влияние утечек и сжимаемость жидкости.
При каждом значении эксцентриситета насоса гидродвигатель будет иметь определенную скорость вращения в установившемся режиме работы. При отсутствии вязкого трения и нагрузки справедливо следующее соотношение:
 .
.
Это уравнение учитывает только расход, выдаваемый насосом. Если же имеется вязкое трение в гидродвигателе или в нагрузке, то для определения действительной скорости вращения гидродвигателя при заданном значении эксцентриситета должен быть использован коэффициент усиления привода по моменту

или

Коэффициент усиления по скорости Kа может быть выражен через конструктивные постоянные системы или через коэффициент усиления по расходу
 ,
,

| (2.1) |
 .
.
Коэффициент усиления по моменту KM можно выразить через коэффициент усиления насоса по давлению или с помощью суммы коэффициентов утечек насоса и гидродвигателя

| (2.1) |
 ,
,
 .
.
Дополнительная величина эксцентриситета, необходимая для того, чтобы создать ускоренное движение инерционной нагрузки, определяется на основании второго закона Ньютона

где

При умножении па квадрат передаточного отношения момент инерции нагрузки приводится к выходному валу гидродвигателя. Уравнение можно записать в следующем виде:
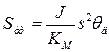
Определим величину эксцентриситета, которая бы обеспечивала расход, компенсирующий сжимаемость жидкости при изменении ускорения нагрузки, сопровождающегося изменением давлений в полостях силового цилиндра. Исследуя выражение, запишем уравнение, определяющее зависимость расхода, компенсирующего сжимаемость, от объемного модуля упругости и объема жидкости
 .
.
Когда исследуется только движение выходного вала привода, перепад давлений H может быть выражен через угловое перемещение θд. Для этого запишем сумму моментов, которые идут на преодоление вязкого трения и сопротивления инерционной нагрузки. Так как момент, развиваемый гидродвигателем, равен произведению удельного объема dд, на перепад давлений H, то

Подставляя уравнение в, получим искомое выражение

Величина общею потребною эксцентриситета определяется как сумма найденных величин
 .
.
Таким образом, общее дифференциальное уравнение системы, получаемое при сложении уравнений, и, будет иметь вид
 .
.
Из уравнения можно получить передаточную функцию привода
 .
.
Передаточную функцию можно представить как

| (2.1) |

где

| (2.1) |


| (2.1) |

Полученное уравнение системы не учитывает люфтов в шестеренчатых передачах и трансмиссиях. При рассмотрении движения вала гидродвигателя механический резонанс будет совпадать с гидравлическим, а при рассмотрении характера движения нагрузки механический и гидравлический резонансы не совпадают.






