ПРОЕКТИРОВАНИЕ УЧЕБНОГО ЗАНЯТИЯ
ПЛАН-КОНСПЕКТ УЧЕБНОГО ЗАНЯТИЯ
| Дата | 20-24.12.2016 |
| Тема | Практическое занятие №15 «Правила дифференцирования» |
| Преподаватель | Лузан Л.О. |
| Профессия / Специальность | |
| Группа | 1503, 1504, 1503к, 1504к |
| Место проведения | корпус №5 |
| Тип занятия | Практическое |
Задачи учебного занятия
| Методические: | - активизация учебно-познавательной деятельности обучающихся через опрос по правилам дифференцирования и выполнение самостоятельной работы - закрепление полученных знаний; - актуализация (ОК1, ОК2, ОК3); |
| Образовательные: | - формирование системы знаний опроизводной - формирование и закрепление навыка вычисления первой производной, составления уравнения касательной - изучить правила дифференцирования второй производной, физический смысл второй производной; - проверить навыки учащихся по нахождению производной; |
| Воспитательные: | - формирование познавательных мотивов - формирование сознательного отношения к обучению, учебной деятельности; |
| Развивающие: | - развитие личностных качеств: внимательность, инициативность; - развитие памяти, развитие логического мышления; |
Методическое обеспечение учебного занятия: рабочая программа (КТП), конспект учебного занятия, раздаточный материал, литература
Периферийное оборудование: компьютер, панель
Структура и содержание учебного занятия
| Этапы учебного занятия | Хронометраж учебного занятия | Деятельность преподавателя | Деятельность обучающихся | |||||||||
| Организационный | 5 минут | Подготовка к занятию, определение готовности к совместной деятельности, проверка наличия тетрадей и ручек.
Цель занятия: актуализировать теоретические знания по нахождению первой производной, полученные на предыдущем уроке. Изучить правила дифференцирования второй производной, а также осуществить проверку знаний обучающихся (самостоятельная работа). Критерии оценивания по формулам:за каждый правильный ответ начисляется 1 балл, за неверный ответ или отсутствие ответа выставляется 0баллов.
Шкала перевода баллов в отметку:
| ||||||||||
| Проверка присутствующих, контроль | ||||||||||||
| Повторение и закрепление материала | 20 минут | 1. Повторение пройденного материала через письменный опрос по формулам дифференцирования. (Приложение №1) (5 мин) 2. Нахождение производных работа у доски Приложение №1 (10 мин) 3. Составление уравнений касательной Приложение №1 (5 мин) | Восприятие и осмысление пройденного материала, актуализация знаний, конспектирование в тетрадях | |||||||||
| Изучение нового материала | 15 минут | Правила дифференцирования второй производной, физический смысл второй производной.
Производные второго и высшего порядка.
Пусть мы нашли для функции y=f(x) ее производную y ¢= f ¢(x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается: 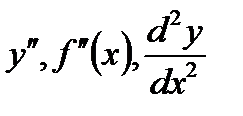 .
Аналогично определяются и обозначаются:
производная третьего порядка - .
Аналогично определяются и обозначаются:
производная третьего порядка - 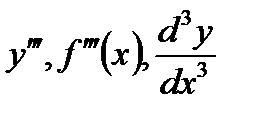 ,
и вообще производная n-го порядка - ,
и вообще производная n-го порядка - 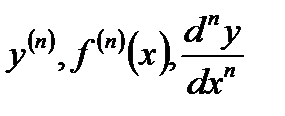 .
Теоретическая часть (устный опрос).
1. В чём заключается механический смысл первой производной?
Ответ. Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке.
2. Если функция задана законом прямолинейного движения S = S(t), то S' (t) –?
Ответ.Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t)
Разберем что есть вторая производная от закона движения?
Ответ. Скорость изменения скорости этого движения, т.е. ускорение а(t) = v' (t) = S' ' (t).
С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х. .
Теоретическая часть (устный опрос).
1. В чём заключается механический смысл первой производной?
Ответ. Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке.
2. Если функция задана законом прямолинейного движения S = S(t), то S' (t) –?
Ответ.Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t)
Разберем что есть вторая производная от закона движения?
Ответ. Скорость изменения скорости этого движения, т.е. ускорение а(t) = v' (t) = S' ' (t).
С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х.
| ||||||||||
| Самостоятельная практическая деятельность | 30 минут | Самостоятельная работа (8 вариантов) (цель: текущий контроль над усвоением знаний, еще раз закрепить знания по правилам дифференцирования, выявить пробелы). (Приложение №1, Самостоятельная работа) | 1. Используя основные формулы дифференцирования, решают самостоятельную работу (30 мин.) (1-6 задание) 2. Составляют уравнение касательной (7 задание) 3. Сдают преподавателю на проверку | |||||||||
| Проверка правильности выполнения самостоятельной работы остается за преподавателем. | ||||||||||||
| Подведение итогов | 5 минут | Теоретические выводы: в результате выполненной работы обучающиеся используют теоретические знания по основным операциям над векторами. | ||||||||||
| Заключительный | 5 минут | Подведение итогов учебного занятия. Итоги по выполнению самостоятельной работы озвучиваются на следующем занятии. | ||||||||||
¡ Домашнее задание. Тело массой 2 кг движется прямолинейно по закону x(t)=t2+t+1. Найти действующую на тело силу F, кинетическую энергию тела через 2с после начала движения.
¡  Найти вторую производную функции: Найти вторую производную функции:
|
1. Таблица производных:
| f(x) | c, где с=const | x | xn | 
| 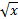
| sinx | cosx | tgx | ctgx | a x | ex | lnx | 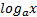
|
| f / (x) | nxn-1 | 
| 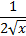
| cosx | -sinx | 
| 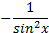
| a xln a | ex | 
| 
|
2. Правила дифференцирования:
(ku)/ = ku/
(u+v)/ = u/ + v/
(uv)/ = u/v + uv/
Практическая часть
1. Используя таблицу производных, правила дифференцирования суммы, произведения и частного элементарных функций, найти производные следующих функций:
2.
 1.1 1.1
|  1.4
1.4
|  1.7
1.7
|
 1.2 1.2
|  1.5 1.5
| 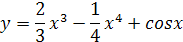 1.8 1.8
|
1.3
у = 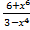
|  1.6
1.6
| 1.9 у = 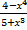
|
Теоретическая часть.
1. В чём заключается механический смысл первой производной?
Ответ. Производная функции у = f(х), в точке х0, выражает скорость изменения функции в этой точке.
2. Если функция задана законом прямолинейного движения S = S(t), то S' (t) –?
Ответ. Скорость движения в момент времени t - это производная по перемещению S' (t) = v(t)
3. Что есть вторая производная от закона движения?
Ответ. Скорость изменения скорости этого движения, т.е. ускорение а(t) = v' (t) = S' ' (t).
С физической точки зрения дифференцирование – определение скорости изменения переменной величины. Производная, таким образом, играет роль скорости изменения зависимой переменной y по отношению к изменению независимой переменной х.
Выясняем формулы из физики, где используется производная.
ü υ(t) = х'(t) – скорость.
ü a(t) = υ'(t) – ускорение.
ü I(t) = q'(t) – сила тока.
ü с(t) = Q'(t) – теплоемкость.
ü d(l) = m'(l) – линейная плотность.
ü K(t) = l'(t) – коэффициент линейного расширения.
ü ω(t) = φ'(t) – угловая скорость.
ü e(t) = ω'(t) – угловое ускорение.
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности.
ü N(t) = A'(t) – мощность.
ü F(x)= A'(x) – Сила есть производная работы по перемещению.
ü Е = Ф'(t) – ЭДС индукции F = р'(t) – 2 закон Ньютона.
| Примеры применения производной в физике | |
| Задача | Решение |
| Тело массой 4 кг движется прямолинейно по закону x(t)=t2+t+1. 1. Какова кинетическая энергия тела в - момент времени 3 сек. после начала движения тела? - конце движения тела? 2. Какова сила, действующая на тело? | 1. Wк = (mv2)/2 x ' (t) = v (t) = 2t+1, v (3) = 7, a(t)= v' (t) = 2, Wк = (4·72)/2=98 2. F = ma, a(t) = v' (t) = x' ' (t), x ' (t) = v (t) = 2t+1, a(t)= v' (t) = 2, F = ma = 4·2 = 8 H. |
| Угол поворота тела вокруг оси изменяется по закону φ(t)=0,1t2-0,5t+0,2. Найти угловую скорость вращения тела в момент времени t=20с. | ω(t) = φ'(t) φ'(t) = 0,2t-0,5 ω(t) = 0,2t-0,5 ω(20) = 3,5 |
| Для любой точки С стержня АВ длиной 10 см, масса куска стержня АС определяется по формуле m(l)=3l2+5l. Найти линейную плотность стержня в середине отрезка АВ, в конце отрезка. | d(l) = m'(l) m'(l) = 6l+5 d(l) = 6l+5 d(5) = 6·5+5=35 – в середине отрезка d(10) = 6·10+5=65 – в конце отрезка |
| Количество электричества, протекающее через проводник, начиная с момента времени t=0, задаётся формулой q=3t2-3t+4. Найти силу тока в конце 6-й секунды. | I(t) = q'(t) q'(t) = 6t-3 I(t) = 6t-3 I(6) = 6·6-3=33 |
Практическая часть.
1.Найти необходимые величины.
| 1.1 S(t)=2t4+3t2-t+√t3 v(t), a(t)-? | 1.6 S(t)=12t 2-(2/3)t3 v(t), a(t)-? | 1.11 S(t)=21t+2t2-(1/3)t3 v(t), a(t)-? |
| 1.2 S(t)=5sin(3t+1), v(t)-? | 1.7 S(t)=6cos(0,5t-4), v(t)-? | 1.12 S(t)=0,5sin(4t+2), v(t)-? |
| 1. 3 x(t)= - 4t2+2t+2, v(1)-? | 1.8 x(t)= √t+2t2 - 3t+2, v(25)-? | 1.13 x(t)=(-1/3)t3+2t2+5t, v(2)-? |
| 1.4 x(t)=t3-4t2, a(5) -? | 1.9 x(t)=0,25t4-2t2, a(1) -? | 1.14 x(t)=t5+3t2-1, a(2) -? |
| 1.5 x(t)=(-1/6)t3 +3t2 – 5, найти t, когда a(t)=0 | 1.10 x(t)=2t3+t-1, найти t, когда a(t)=2 | 1.15 x(t)= (-1/3)t3+2t2+5t, найти t, когда v(t)=0 |
2. Решить задачу.
2.1 Найти силу F, действующую на материальную точку с массой m, движущуюся прямолинейно по закону s(t) = 2t3-t2, при t=2.
2.2 Тело массой 2 кг движется прямолинейно по закону x(t)=t2+t+1. Найти действующую на тело силу F, кинетическую энергию тела через 2с после начала движения.
2.3 Маховик, задерживаемый тормозом, за время t поворачивается на угол φ(t)=4t-0,3t2. Найти угловую скорость ω(t) вращения маховика в момент времени 2 с.
2.4 Точка движется по закону x(t)=√t. Найти её скорость в момент времени 4с.
2.5 Найти скорость тела, движущегося по закону s(t)=3t+5.
2.6 Тело движется прямолинейно по закону s(t)=2t2-t+4. Найти скорость тела в моменты времени t1=0, t2=2, t3=5 с.
2.7 Найти скорость движения точки в момент времени t=5с, если закон движения задан формулой s(t)=3t2-2t+5.
2.8 Тело движется прямолинейно по закону s (t)=1-2t+t3. Найти скорость и ускорение в момент времени t=3с.
2.9 Найти скорость и ускорение движения тела в момент времени t=2с, если закон движения задан формулой s=4t2-3.
2.10 Когда скорость точки, движущейся прямолинейно по закону s(t)=t2-4t+5, равна 0?
2.11 Сила тока изменяется по закону I=0,4t2. Найти скорость изменения силы тока в конце 8-й секунды.
2.12 Изменение силы тока в зависимости от времени задано уравнением I = 2t2-5t. Найти скорость изменения силы тока в конце 10-й секунды.
2.13 Количество теплоты Q, получаемое некоторым веществом при нагревании определяется по формуле Q=10t+0,5t2. Найти теплоёмкость этого вещества при 20 К.
Производная функций. Информационная карта с алгоритмом решения
Вариант №1
| № п/п | Формула производной | Задания для самостоятельного решения |
| Если у=С, где С-const (постоянная), то y'=(C)'=0 Пример:1) у=6 (т.е. С=6), тогда y'=(6)'=0 2) у=-0,81 (т.е. С=0,81), тогда y'=(0,81)'=0 | 1) у=31 2) у=-1/3 | |
| Если у=сх, где С-const (постоянная), то y'=(сх)'=с Пример:1) у=5х (т.е. С=5), тогда y'=(5х)'=5 2) у=-3х (т.е. С=-3), тогда y'=(-3х)'=-3 3) у=2х/5 (т.е. С=2/5), тогда y'=(2х/5)'=2/5 | 1) у=17х 2) у=-0,2х 3)у=х/3 | |
Если у=х  (где n, где n (где n, где n  N, n≥2), то y'= nх N, n≥2), то y'= nх  .
Пример: 1) .
Пример: 1)  (т.е. n=10), тогдаy' (т.е. n=10), тогдаy' 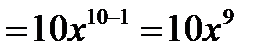 2)
2) (т.е. n=2), тогдаy' (т.е. n=2), тогдаy' 
| 1) у=  2) у=
2) у= 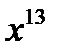 3) у=-
3) у=- 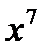
| |
Если у=cх  (где n, где n (где n, где n  N, n≥2, С-const), то y'= с·nх N, n≥2, С-const), то y'= с·nх  Пример:
1)
Пример:
1)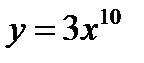 (т.е. n=10, с=3), тогдаy' (т.е. n=10, с=3), тогдаy' 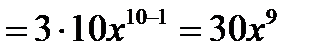 2)
2) (т.е. n=2, с=- (т.е. n=2, с=- 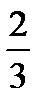 ), тогдаy' ), тогдаy' 
| 1) у=  2) у=
2) у= 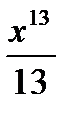 3) у=-0,5
3) у=-0,5 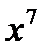
| |
Если y'=(u+v)', где u, v –функции, то y'=u'+v'
Пример:
1) (т.е. u= (т.е. u= 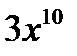 , v=3), тогдаy' , v=3), тогдаy'  2)
2)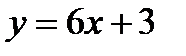 (т.е. u=6x, v=3), тогдаy'= (т.е. u=6x, v=3), тогдаy'= 
| 1) y=1-2x
2) y=13x  3) y=5x
3) y=5x 
| |
Если y=u·v, где u, v –функции, то y'=u'v+uv'
Пример:
1) (т.е. u= (т.е. u=  , v= , v= 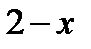 ), тогда
у'=(6х-3)'(2-х)+(6х-3)(2-х)'=6(2-х)+(6х-3)(-1)=12-6х-6х+3=-12х+15
2) у=3х ), тогда
у'=(6х-3)'(2-х)+(6х-3)(2-х)'=6(2-х)+(6х-3)(-1)=12-6х-6х+3=-12х+15
2) у=3х 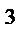 (х+5) (т.е. u=3x (х+5) (т.е. u=3x  , v=x+5), тогда
у'=(3x , v=x+5), тогда
у'=(3x  )'(х+5)+ 3x )'(х+5)+ 3x  (х+5)'=3·3х (х+5)'=3·3х 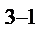 (х+5) +3x (х+5) +3x  ·1=9x ·1=9x  (х+5)+ 3x (х+5)+ 3x  =9x =9x  +45x +45x 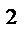 +3x +3x  =12x =12x  +45x +45x 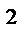
| 1) у=(5-2х)(3х+1)
2) у= 7 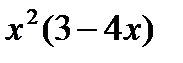 3) y=(x
3) y=(x 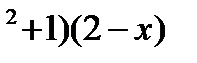
| |
Если y=  , где u, v –функции, v , где u, v –функции, v  , то , то 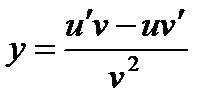 Пример:
1)
Пример:
1) 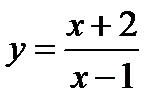 (т.е. u=х+2, v=х-1), тогда (т.е. u=х+2, v=х-1), тогда 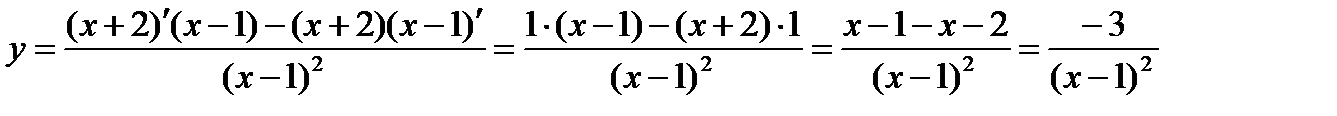
| 1) 
| |
Уравнение касательной к графику функции y = f(x) в точке  имеет вид: имеет вид:  Алгоритм составления уравнения касательной к графику функции y = f(x)1. Обозначить буквой Алгоритм составления уравнения касательной к графику функции y = f(x)1. Обозначить буквой  абсциссу точки касания. 2. Найти f( абсциссу точки касания. 2. Найти f(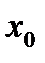 ). 3. Найти f '(x) и f '( ). 3. Найти f '(x) и f '( ). 4. Подставить найденные числа a, f(x), f '( ). 4. Подставить найденные числа a, f(x), f '( ) в общее уравнение касательной y - f( ) в общее уравнение касательной y - f( ) = f '(x)(x – ) = f '(x)(x –  ). Примеры составления уравнения касательной. Пример 1. Составьте уравнение касательной в точке ). Примеры составления уравнения касательной. Пример 1. Составьте уравнение касательной в точке  =3 к графику функции =3 к графику функции 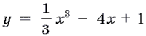 Решение1. a = 3 – абсцисса точки касания. 2. f(3) = – 2. 3. f '(x) = x2 – 4, f '(3) = 5. y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.
Решение1. a = 3 – абсцисса точки касания. 2. f(3) = – 2. 3. f '(x) = x2 – 4, f '(3) = 5. y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.
|
Задание для практической работы по теме «Вычисление производных функций»: Вычислить производные функций:
| Вариант 1 | Вариант 2 | Вариант 3 |
1. y= =x3-15
2. y=-3x3+5х-8+4x2
3. y=(x3-1)(x+1)
4. y=(x3-2)(3x+1)
5.  6.
6.  7. Y=3x3-x,
7. Y=3x3-x, 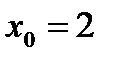
| 1. y= =2x2-1
2. y= x3+6х-18+6x2
3. y=(x2+1)(x-5)
4. y=(x3+2)(7x-3)
5.  6.
6. 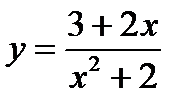 7. Y=-x3+x,
7. Y=-x3+x, 
| 1. y= =8x2+х
2. y= x4+5х-1+2x2
3. y=(x2+2)(x+5)
4. y=(x3+2х)(x+15)
5. 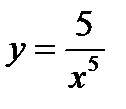 6.
6.  7. Y=-3x2+12x,
7. Y=-3x2+12x, 
|
| Вариант 4 | Вариант 5 | Вариант 6 |
1. y= =3x3-5
2. y= 5x3+5-8х+x2
3. y=(x3-7)(2x+1)
4. y=(x3-6)(x+1)
5.  6.
6. 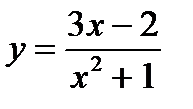 7. Y=x2+5x+4,
7. Y=x2+5x+4, 
| 1. y= =4x2+5х
2. y=x4+х-10+5x2
3. y=(x2-5)(x+2)
4. y=(3x3+х)(x-5)
5. 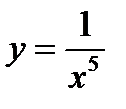 6.
6.  7. Y=-x2+2x+15,
7. Y=-x2+2x+15, 
| 1. y= =2x3-х
2. y= 4x3+5х-8+2x2
3. y=(x3-1)(x+2)
4. y=(x3-2)(2x+1)
5.  6.
6. 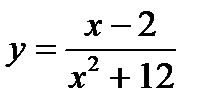 7. Y=1/3x3-9,
7. Y=1/3x3-9, 
|
| Вариант 7 | Вариант 8 | Вариант 9 |
1.  2. у=15x3+6-2х+x2
3. y=-8x2(х+1)
4. y=4x(1-2x-2x2)
5. y=sin x/ln x
6.
2. у=15x3+6-2х+x2
3. y=-8x2(х+1)
4. y=4x(1-2x-2x2)
5. y=sin x/ln x
6. 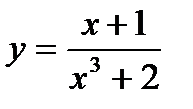  7. Y=3x3-x,
7. Y=3x3-x, 
| 1. Y=3x -5
2. у=2x4+5х-10+5x2
3. y=-2x(5x+3)
4. y=(3x-5)(5-x2)
5. 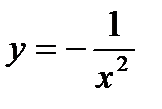 6. y=cos x·2x
7. Y=-x3+x,
6. y=cos x·2x
7. Y=-x3+x, 
| 1. y= =-3x3
2. y= 3x3+15х-8+x2
3. y=(x3-1)(x+1)
4. y=5x ·tg x
5. 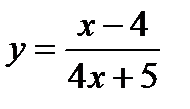 6.
6.  7. Y=-3x2+12x,
7. Y=-3x2+12x, 
|






