Отсев заведомо лишних чисел

Как быстро извлекать квадратные корни

Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:

1. Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
2. Существует алгоритм, с помощью которого эти корни считаются почти устно.

Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней.

Итак, алгоритм:

1. Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
2. Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
3. Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.

Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.

Ограничение корней

В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:

10² = 100;
20² = 400;
30² = 900;
40² = 1600;
...
90² = 8100;
100² = 10 000.

Получим ряд чисел:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:

То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:

Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.

Отсев заведомо лишних чисел

Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.

Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:

Последняя цифра квадрата зависит только от последней цифры исходного числа.

Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.

Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:

Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:

2² = 4;
8² = 64 → 4.

Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:

Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:

Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!

Финальные вычисления

Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.

Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:

52² = (50 +2)² = 2500 + 2 · 50 · 2 + 4 = 2704;
58² = (60 − 2)² = 3600 − 2 · 60 · 2 + 4 = 3364.

Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный:)

Примеры вычисления корней

Теория — это, конечно, хорошо. Но давайте проверим ее на практике.

Задача. Вычислите квадратный корень:

Для начала выясним, между какими числами лежит число 576:

400 < 576 < 900
20² < 576 < 30²

Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:

24; 26.

Осталось возвести каждое число в квадрат и сравнить с исходным:

24² = (20 + 4)² = 576

Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.

Задача. Вычислите квадратный корень:

Здесь и далее я буду писать только основные шаги. Итак, ограничиваем число:

900 < 1369 < 1600;
30² < 1369 < 40^2;

Смотрим на последнюю цифру:

1369 → 9;
33; 37.

Возводим в квадрат:

33² = (30 + 3)² = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
37² = (40 − 3)² = 1600 − 2 · 40 · 3 + 9 = 1369.

Вот и ответ: 37.

Задача. Вычислите квадратный корень:

Ограничиваем число:

2500 < 2704 < 3600;
50² < 2704 < 60^2;

Смотрим на последнюю цифру:

2704 → 4;
52; 58.

Возводим в квадрат:

52² = (50 + 2)² = 2500 + 2 · 50 · 2 + 4 = 2704;

Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.

Задача. Вычислите квадратный корень:

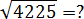
Ограничиваем число:

3600 < 4225 < 4900;
60² < 4225 < 70^2;

Смотрим на последнюю цифру:

4225 → 5;
65.

Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:

65² = (60 + 5)² = 3600 + 2 · 60 · 5 + 25 = 4225;

Все правильно. Записываем ответ.

Заключение

Многие спрашивают: зачем вообще считать такие корни? Не лучше ли взять калькулятор и не парить себе мозг?

Увы, не лучше. Давайте разберемся в причинах. Их две:

• На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
• Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.

В общем, учитесь считать. И все будет хорошо. Удачи!