Определение расстояний перевозки

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе

по дисциплине

«Взаимодействие видов транспорта при смешанных перевозках»

 

Выполнил студент гр.355 Егоров

Руководитель проекта Потапов

 

 

САМАРА 2012

РЕФЕРАТ

Пояснительная записка 34 стр., 2 рис., 18 табл., 2 источника.

ГРУЗ, ПЕРЕВОЗКА, ВИД ТРАНСПОРТА, ПУНКТ ОТПРАВЛЕНИЯ, ПУНКТ ВЗАИМОДЕЙСТВИЯ, ПУНКТ НАЗНАЧЕНИЯ, ПРОМЕЖУТОЧНЫЙ ПУНКТ, ПЕРЕВАЛКА, МАРШРУТ, МАТРИЦА РАССТОЯНИЙ, ЗАПАС ГРУЗА, ПЕРЕРАБАТЫВАЕМАЯ МОЩНОСТЬ, ЗАЯВКА, СЕБЕСТОИМОСТЬ ПЕРЕВОЗКИ, ЦЕЛЕВАЯ ФУНКЦИЯ

Определены кратчайшие расстояния от пунктов отправления до пунктов взаимодействия, а также себестоимости перевозки:

– из пунктов отправления в пункты взаимодействия;

– из пунктов отправления в пункты назначения;

– из пунктов взаимодействия в пункты назначения.

Получен план перевозок, обеспечивающий минимальные затраты.

СОДЕРЖАНИЕ

РЕФЕРАТ. 2

СОДЕРЖАНИЕ. 4

ВВЕДЕНИЕ. 5

1 ПОСТАНОВКА ЗАДАЧИ.. 6

2 ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ ПЕРЕВОЗКИ.. 9

2.1 Пункты отправления – пункты назначения (первый вид транспорта) 9

2.2 Пункты взаимодействия – пункты назначения (второй вид транспорта) 9

2.3 Пункты отправления – пункты взаимодействия (первый вид транспорта) 10

2.3.1 Пункт D₄ 10

2.3.2 Пункт D₃ 17

3 ОПРЕДЕЛЕНИЕ СЕБЕСТОИМОСТИ ПЕРЕВОЗКИ.. 24

3.1 Первый вид транспорта. 24

3.2 Второй вид транспорта. 25

4 РЕШЕНИЕ ЗАДАЧИ.. 27

ЗАКЛЮЧЕНИЕ. 33

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 34

ВВЕДЕНИЕ

В данной курсовой работе необходимо определить кратчайшие расстояния от пунктов отправления до пунктов взаимодействия, рассчитать себестоимости перевозки из пунктов отправления в пункты взаимодействия, из пунктов отправления в пункты назначения и из пунктов взаимодействия в пункты назначения и затем получить план перевозок, обеспечивающий минимальные затраты.

ПОСТАНОВКА ЗАДАЧИ

Имеется семь пунктов отправления однородного груза с заданными объемами его запасов. Имеется два пункта назначения с заданными заявками на получение груза. Доставка может осуществляться одним видам транспорта прямым сообщением или двумя видами с перевалкой с первого вида транспорта на второй в двух пунктах взаимодействия с заданными перерабатывающими способностями.

Необходимо составить такой план перевозок, чтобы во все пункты назначения заданное количество груза было доставлено, а общая себестоимость перевозок была минимальна.

Введем переменные для описания задачи:

k = 6 - количество пунктов отправления;

m = 4 - количество пунктов взаимодействия;

n = 2 - количество пунктов назначения;

Х_ki - количество груза, перевозимого из k-го пункта отправления в i-й пункт взаимодействия первым видом транспорта, т, k = 1...6, i = 1...4;

Y_ij - количество груза, перевозимого из i-ro пункта взаимодействия в j-й пункт назначения вторым видом транспорта, т, i = 1...4, j = 1...2;

Z_kj - количество груза, перевозимого в прямом сообщении из k-го пункта отправления в j-й пункт назначения первым видом транспорта, т, k = 1...6, j = 1...2;

А_k - запас груза в k-ом пункте отправления, т, k = 1...6;

D_i - перерабатывающая способность i-ro пункта взаимодействия, т, i = 1...3;

B_j - заявка на груз для j-го пункта назначения, т, j = 1...2;

- себестоимость перевозки 1 тонны груза из k-гопункта отправления в i-й пункт взаимодействия первым видом транспорта с учетом затрат на перевалку, руб./т,k=1...6, i=l...4;

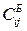- себестоимость перевозки 1 тонны груза из i-ro пункта взаимодействия в j-й пункт назначения вторым видом транспорта, руб./т, i = 1...4, j = l...2;

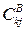- себестоимость перевозки 1 тонны груза в прямом сообщении из k-го пункта отправления в j-й пункт назначения первым видом транспорта, руб./т, k = 1...6,j = 1...2;

Значения переменных А_k, D_i,B_j известны и входят в состав исходных данных; значения переменных , , 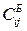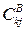рассчитываются; значения переменных Х_ki, Y_ij, Z_kj определяются в ходе решения задачи.

Целевая функция (суммарная себестоимость перевозок) записывается сле­дующим образом:

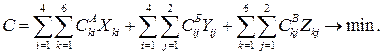(1)

Необходимым условием решения данной задачи является следующее (суммарный запас груза в пунктах отправки должен быть не меньше суммы заявок пунк­тов назначения):

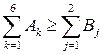(2)

Ограничения, накладываемые на задачу, формализуются в следующем виде.

1. Суммарное количество груза, прибывающего в j-й пункт назначения из пунктов взаимодействия и из пунктов отправления прямым сообщением, должно быть равно заявке этого пункта:

(3)

2. Суммарное количество груза, отправляемого из i-ro пункта взаимодействия, должно быть равно суммарному количеству груза, прибывающего в этот пункт:

(4)

3. Суммарное количество груза, прибывающего в i-й пункт взаимодействия, неможет превышать перерабатывающей способности этого пункта:

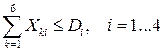(5)

4. Суммарное количество груза, отправляемого из k-ого пункта отправления впункты взаимодействия и в пункты назначения прямым сообщением, не может превышать запас груза в этом пункте:

(6)

Сформулированная задача является многопараметрической задачей линейного программирования минимизации критерия (1) с учетом выполнения условия (2) и ограничений (3), (4), (5), (6).

ОПРЕДЕЛЕНИЕ РАССТОЯНИЙ ПЕРЕВОЗКИ

2.1Пункты отправления – пункты назначения (первый вид транспорта)

Как следует из исходных данных, каждый пункт назначения связан с каждым пунктом отправления единственным прямым маршрутом. Следовательно, расстояния между этими пунктами совпадают с расстояниями, приведенными в матрице расстояний между пунктами (таблица 1).

 

Таблица 1 - Расстояния между пунктами отправления и назначения

Расстояние, км	Пункты назначения
B1	B2
Пункты отправления	A1
A2
A3
A4
A5
A6

2.2Пункты взаимодействия – пункты назначения (второй вид транспорта)

Как следует из исходных данных, каждый пункт назначения связан с каждым пунктом взаимодействия единственным прямым маршрутом. Следовательно, расстояния между этими пунктами совпадают с расстояниями, приведенными в матрице расстояний между пунктами (таблица 2).

 

Таблица 2 – Расстояния между пунктами взаимодействия и назначения

Расстояние, км	Пункты назначения
B1	B2
Пункты взаимодействия	D1
D2
D3
D4

2.3Пункты отправления – пункты взаимодействия (первый вид транспорта)

Из матрицы расстояний видно, что прямых маршрутов между пунктами А_k (k = 1...6) отправления и пунктами D_i (i = 3...4) взаимодействия нет. Необходимо построить кратчайшие маршруты, пролегающие через промежуточные пункты E_s (s = 1...9), и определить длины этих маршрутов.

Сформируем матрицу расстояний между пунктами А_k отправления, промежуточными пунктами E_s, пунктами D_i взаимодействия; введем сквозную нумерацию узлов (таблица 3).

 

Таблица 3 – Матрица расстояний между пунктами отправления, взаимодействия и промежуточными пунктами

Пункты

A1

A2

A3

A4

E1

E2

E3

E4

E5

E6

E7

E8

E9

D1

D2

D3

D4

Узлы

A1

A2

A3

A4

E1

E2

E3

E4

E5

E6

E7

E8

E9

D1

D2

D3

D4

 

2.3.1 Пункт D₄

Построим маршруты в узел 17 (пункт D₄) из узлов 1 (пункт А₁), 2 (пункт А₂), 3 (пункт А₃), 4 (пункт А₄).

1). Приближение k=0.

Определим длины прямых (без посещения промежуточных узлов) маршрутов в узел 17. Для каждого j-гo узла (j = 10, 12), который соединен дугой с узлом 17 (т.е. имеется прямой маршрут), длина кратчайшего маршрута принимается равной расстоянию между этим узлом и узлом 17; для остальных узлов значения принимаются равными бесконечности:

Полученные маршруты и значения их длин занесем в таблицу 7.

2) Приближение k=1.

Определим длину L¹_i-j возможного маршрута из i-го узла в узел 17, проходящего через j-й узел, с числом промежуточных узлов не более одного как сумму расстояния L_i-jот i-го узла до j-го узла и длины U⁰_j прямого маршрута из этого узла в узел 17:

L¹_i-j= L_i-j+ U⁰_j, i = 1, 2, … 16, j = 1,2, … 17, i ≠ 17, j ≠ i.

В качестве длины кратчайшего маршрута из i-го узла в узел 17 принимается минимальное из возможных значений:

U¹_j= min{L¹_i-j}.

 

Таблица 4 – Маршруты в узел 17 с числом промежуточных узлов не более одного

Из узла 3	j	L3-j	U0j	L13-j	U13
3-10-17	10	20	33	53	53
Из узла 4	j	L4-j	U0j	L14-j	U14
4-10-17	10	11	33	44	44
Из узла 8	j	L8-j	U0j	L18-j	U18
8-12-17	12	12	9	21	21
Из узла 10	j	L10-j	U0j	L110-j	U110
10-17	15			33	33
Из узла 11	j	L11-j	U0j	L111-j	U111
11-10-17
11-12-17	12	9	9	18	18
Из узла 12	j	L12-j	U0j	L112-j	U112
12-17	15			9	9
Из узла 13	j	L13-j	U0j	L113-j	U113
13-10-17
13-12-17	12	15	9	24	24

 

Полученные кратчайшие маршруты из каждого узла в узел 17 и значения их длин U¹_j (выделенные заливкой) занесем в таблицу 7.

3) Приближение k = 2.

Определим длину L²_i-j возможного маршрута из i-го узла в узел 17, проходящего через j-й узел, с числом промежуточных узлов не более двух как сумму расстояния L_i-jот i-го узла до j-го узла и длины U¹_j маршрута из j-го узла в узел 17 с числом узлов не более одного:

L²_i-j= L_i-j+ U¹_j, i = 1, 2, … 16, j = 1,2, … 17,i ≠ 17,j ≠ i.

В качестве длины кратчайшего маршрута из i-го узла в узел 17 принимается минимальное из возможных значений:

U²_j= min{L²_i-j}.

 

Таблица 5 – Маршруты в узел 17 с числом промежуточных узлов не более двух

Из узла 1	j	L1-j	U1j	L11-j	U21
1-8-12-17	8	16	21	37	37
Из узла 2	j	L2-j	U1j	L12-j	U22
2-8-12-17	8	9	21	30	30
Из узла 3	j	L3-j	U1j	L13-j	U23
3-10-17	10	20	33	53	53
Из узла 4	j	L4-j	U1j	L14-j	U24
4-10-17	10	11	33	44	44
Из узла 6	j	L6-j	U1j	L16-j	U26
6-11-12-17	11	12	18	30	30
Из узла 7	j	L7-j	U1j	L17-j	U27
7-8-12-17	8	11	21	32	32
7-11-12-17
Из узла 8	j	L8-j	U1j	L18-j	U28
8-12-17	12	12	9	21	21
8-13-12-17
Из узла 9	j	L9-j	U1j	L19-j	U29
9-3-10-17
9-8-12-17	8	4	21	25	25
9-13-12-17
Из узла 10	j	L10-j	U1j	L110-j	U210
10-17
10-11-12-17	11	6	18	24	24
10-13-12-17
Из узла 11	j	L11-j	U1j	L111-j	U211
11-12-17	12	9	9	18	18
11-10-17
Из узла 12	j	L12-j	U1j	L112-j	U212
12-17	15			9	9
Из узла 13	j	L13-j	U1j	L113-j	U213
13-8-12-17
13-10-17
13-12-17	12	15	9	24	24
Из узла 15	j	L15-j	U0j	L115-j	U215
15-13-12-17	13	7	24	31	31

 

Полученные кратчайшие маршруты из каждого узла в узел 17 и значения их длин U²_j (выделенные заливкой) занесем в таблицу 7.

4). Приближение k=3.

Определим длину L³_i-j возможного маршрута из i-го узла в узел 17, проходящего через j-й узел, с числом промежуточных узлов не более трех как сумму расстояния L_i-jот i-го узла до j-го узла и длины U²_j маршрута из j-го узла в узел 17 с числом узлов не более двух:

L³_i-j= L_i-j+ U²_j, i = 1, 2, … 16, j = 1,2, … 17,i ≠ 17,j ≠ i.

В качестве длины кратчайшего маршрута из i-го узла в узел 17 принимается минимальное из возможных значений:

U³_j= min{L³_i-j}.

 

Таблица 6 – Маршруты в узел 17 с числом промежуточных узлов не более трех

Из узла 1	j	L1-j	U2j	L11-j	U31
1-7-8-12-17
1-8-12-17	8	16	21	37	37
Из узла 2	j	L2-j	U2j	L12-j	U32
2-8-12-17	8	9	21	30	30
2-9-8-12-17
Из узла 3	j	L3-j	U2j	L13-j	U33
3-10-17
3-9-8-12-17	9	9	25	34	34
Из узла 4	j	L4-j	U2j	L14-j	U34
4-10-17
4-10-11-12-17	10	11	24	35	35
Из узла 5	j	L5-j	U2j	L15-j	U35
5-6-11-12-17	6	3	30	33	33
Из узла 6	j	L6-j	U2j	L16-j	U36
6-11-12-17	11	12	18	30	30
6-7-8-12-17
Из узла 7	j	L7-j	U2j	L17-j	U37
7-8-12-17	8	11	21	32	32
7-1-8-12-17
7-6-11-12-17
7-11-12-17
Из узла 8	j	L8-j	U2j	L18-j	U38
8-12-17	12	12	9	21	21
Из узла 9	j	L9-j	U2j	L19-j	U39
9-8-12-17	8	4	21	25	25
9-2-8-12-17
9-3-10-17
9-13-12-17
Из узла 10	j	L10-j	U2j	L110-j	U310
10-11-12-17	11	6	18	24	24
10-13-12-17
Из узла 11	j	L11-j	U2j	L111-j	U311
11-12-17	12	9	9	18	18
11-7-8-12-17
Из узла 12	j	L12-j	U2j	L112-j	U312
12-17
Из узла 13	j	L13-j	U2j	L113-j	U313
13-12-17	12	15	9	24	24
13-8-12-17
13-9-8-12-17
13-10-11-12-17
Из узла 15	j	L15-j	U0j	L115-j	U215
15-13-12-17	13	7	24	31	31

 

Полученные кратчайшие маршруты из каждого узла в узел 17 и значения их длин U³_j (выделены заливкой) занесем в таблицу 7.

5) Приближение k=4.

Определим длину L⁴_i-j возможного маршрута из i-гo узла в узел 17, проходящего через j-й узел, с числом промежуточных узлов не более четырех, как сумму расстояния L_i-jот i-го узла до j-го узла и длины U³_j маршрута из j-го узла в узел 17 с числом узлов не более трех:

L⁴_i-j= L_i-j+ U³_j, i = 1, 2, … 16, j = 1,2, … 17,i ≠ 17,j ≠ i.

В качестве длины кратчайшего маршрута из i-го узла в узел 17 принимается минимальное из возможных значений:

U⁴_j= min{L⁴_i-j}.

Результаты расчетов показывают, что длины кратчайших маршрутов U⁴_j с числом промежуточных узлов не более четырех оказываются равными длинам кратчайших маршрутов U³_j с числом промежуточных узлов не более трех. В связи с этим дальнейшие расчеты прекращаются.

В таблице 7 для каждого приближения приведены полученные кратчайшие маршруты в узел 17 и их длины.

 

Таблица 7 – Кратчайшие маршруты в узел 17

j	k=0	k=1	k=2
Маршрут	U0j	Маршрут	U1j	Маршрут	U2j
					1-8-12-17
					2-8-12-17
			3-10-17		3-10-17
			4-10-17		4-10-17
			8-12-17
					6-11-12-17
			10-17		7-8-12-17
			11-12-17		8-12-17
			12-17		9-8-12-17
	10-17		13-12-17		10-11-12-17
					11-12-17
	12-17				12-17
					13-12-17
					14-11-12-17
					15-13-12-17

 

j	k=3	k=4
Маршрут	U3j	Маршрут	U4j
	1-8-12-17		1-8-12-17
	2-8-12-17		2-8-12-17
	3-9-8-12-17		3-9-8-12-17
	4-10-11-12-17		4-10-11-12-17
	5-6-11-12-17		5-6-11-12-17
	6-11-12-17		6-11-12-17
	7-8-12-17		7-8-12-17
	8-12-17		8-12-17
	9-8-12-17		9-8-12-17
	10-11-12-17		10-11-12-17
	11-12-17		11-12-17
	12-17		12-17
	13-12-17		13-12-17
	14-11-12-17		14-11-12-17
	15-13-12-17		15-13-12-17

 

Искомые кратчайшие маршруты в узел 17 (пункт D₄)

из узла 1 (пункт A₁): 1-8-12-17(A₁-E₄-E₈-D₄); расстояние –37;

из узла 2 (пункт А₂): 2-8-12-17(A₂-E₄-E₈-D₄); расстояние – 30;

из узла 3 (пункт А₃): 3-9-8-12-17(A₃-E₅-E₄-E₈-D₄); расстояние –34;

из узла 4 (пункт А₄): 4-10-11-12-17 (A₄-E₆-E₇-E₈-D₄); расстояние –35.

2.3.2 Пункт D₃

Построим маршруты в узел 16 (пункт D₃) из узлов 1 (пункт А₁), 2 (пункт А₂), 3 (пункт А₃), 4 (пункт А₄).

1). Приближение k=0.

Определим длины прямых (без посещения промежуточных узлов) маршрутов в узел 16. Для каждого j-гo узла (j = 11, 13), который соединен дугой с узлом 16 (т.е. имеется прямой маршрут), длина кратчайшего маршрута принимается равной расстоянию L_j-16 между этим узлом и узлом 16; для остальных узлов значения принимаются равными бесконечности:

;

Полученные маршруты и значения их длин занесем в таблицу 12.

2) Приближение k=1.

Определим длину L¹_i-j возможного маршрута из i-го узла в узел 16, проходящего через j-й узел, с числом промежуточных узлов не более одного как сумму расстояния L_i-jот i-го узла до j-го узла и длины U⁰_j прямого маршрута из этого узла в узел 16:

L¹_i-j= L_i-j+ U⁰_j, i = 1, 2, … 15, j = 1,2, … 16, j ≠ i,j ≠ 16.

В качестве длины кратчайшего маршрута из i-го узла в узел 16 принимается минимальное из возможных значений:

U¹_j= min{L¹_i-j}.

 

Таблица 8 – Маршруты в узел 16 с числом промежуточных узлов не более одного

Из узла 6	j	L6-j	U0j	L16-j	U16
6-11-16	11	12	12	24	24
Из узла 7	j	L7-j	U0j	L17-j	U17
7-11-16	11	40	12	52	52
Из узла 8	j	L8-j	U0j	L18-j	U18
8-13-16	13	10	22	32	32
Из узла 9	j	L9-j	U0j	L19-j	U19
9-13-16	13	9	22	31	31
Из узла 10	j	L10-j	U0j	L110-j	U110
10-11-16	11	6	12	18	18
10-13-16
Из узла 11	j	L11-j	U0j	L111-j	U111
11-16	16			12	12
Из узла 12	j	L12-j	U0j	L112-j	U112
12-11-16	11	9	12	21	21
12-13-16
Из узла 13	j	L13-j	U0j	L113-j	U113
13-16	16			22	22
Из узла 14	j	L14-j	U0j	L114-j	U114
15-13-16	13	7	22	29	29

 

Полученные кратчайшие маршруты из каждого узла в узел 16 и значения их длин U¹_j (выделенные заливкой) занесем в таблицу 12.

3) Приближение k = 2.

Определим длину L²_i-j возможного маршрута из i-го узла в узел 16, проходящего через j-й узел, с числом промежуточных узлов не более двух как сумму расстояния L_i-jот i-го узла до j-го узла и длины U¹_j маршрута из j-го узла в узел 16 с числом узлов не более одного:

L²_i-j= L_i-j+ U¹_j, i = 1, 2, … 15, j = 1,2, … 16, j ≠ i,j ≠ 16.

В качестве длины кратчайшего маршрута из i-го узла в узел 16 принимается минимальное из возможных значений:

U²_j= min{L²_i-j}.

 

Таблица 9 – Маршруты в узел 16 с числом промежуточных узлов не более двух

Из узла 1	j	L1-j	U1j	L11-j	U21
1-7-11-16
1-8-13-16	8	16	32	48	48
Из узла 2	j	L2-j	U1j	L12-j	U22
2-8-13-16	8	9	32	41	41
2-9-13-16
Из узла 3	j	L3-j	U1j	L13-j	U23
3-9-13-16
3-10-11-16	10	20	18	38	38
Из узла 4	j	L4-j	U1j	L14-j	U24
4-10-11-16	10	11	18	29	29
Из узла 5	j	L5-j	U1j	L15-j	U25
5-6-11-16	6	3	24	27	27
Из узла 6	j	L6-j	U1j	L16-j	U26
6-11-16	11	12	12	24	24
6-7-11-16
Из узла 7	j	L7-j	U1j	L17-j	U27
7-11-16
7-6-11-16	6	9	24	33	33
7-8-13-16
Из узла 8	j	L8-j	U1j	L18-j	U28
8-13-16	13	10	22	32	32
8-7-11-16
8-9-13-16
8-12-11-16
Из узла 9	j	L9-j	U1j	L19-j	U29
9-13-16	13	9	22	31	31
9-8-13-16
Из узла 10	j	L10-j	U1j	L110-j	U210
10-11-16	11	6	12	18	18
Из узла 11	j	L11-j	U1j	L111-j	U211
11-16	16			12	12
Из узла 12	j	L12-j	U1j	L112-j	U212
12-11-16	11	9	12	21	21
12-8-13-16
Из узла 13	j	L13-j	U1j	L113-j	U213
13-16
13-10-11-16	10	2	18	20	20
13-12-11-16
Из узла 15	j	L15-j	U1j	L115-j	U215
15-13-16	13	7	22	29	29

 

 

Полученные кратчайшие маршруты из каждого узла в узел 16 и значения их длин U²_j (выделенные заливкой) занесем в таблицу 12.

4) Приближение k=3.

Определим длину L³_i-j возможного маршрута из i-го узла в узел 16, проходящего через j-й узел, с числом промежуточных узлов не более трех как сумму расстояния L_i-jот i-го узла до j-го узла и длины U²_j маршрута из j-го узла в узел 16 с числом узлов не более двух:

L³_i-j= L_i-j+ U²_j, i = 1, 2, … 15, j = 1,2, … 16, j ≠ i,j ≠ 16.

В качестве длины кратчайшего маршрута из i-го узла в узел 16 принимается минимальное из возможных значений:

U³_j= min{L³_i-j}.

 

Таблица 10 – Маршруты в узел 16 с числом промежуточных узлов не более трех

Из узла 1	j	L1-j	U2j	L11-j	U31
1-8-13-16
1-7-6-11-16	7	5	33	38	38
Из узла 2	j	L2-j	U2j	L12-j	U32
2-8-13-16	8	9	32	41	41
Из узла 3	j	L3-j	U2j	L13-j	U33
3-10-11-16	10	20	18	38	38
Из узла 4	j	L4-j	U2j	L14-j	U34
4-10-11-16	10	11	18	29	29
Из узла 5	j	L5-j	U2j	L15-j	U35
5-6-11-16	6	3	24	27	27
Из узла 6	j	L6-j	U2j	L16-j	U36
6-11-16	11	12	12	24	24
Из узла 7	j	L7-j	U2j	L17-j	U37
7-1-8-13-16
7-6-11-16	6	9	24	33	33
Из узла 8	j	L8-j	U2j	L18-j	U38
8-13-16
8-7-6-11-16
8-13-10-11-16	13	10	20	30	30
Из узла 9	j	L9-j	U2j	L19-j	U39
9-13-16
9-2-8-13-16
9-3-10-11-16
9-13-10-11-16	13	9	20	29	29
Из узла 10	j	L10-j	U2j	L110-j	U310
10-11-16	11	6	12	18	18
Из узла 11	j	L11-j	U2j	L111-j	U311
11-16	16			12	12
Из узла 12	j	L12-j	U2j	L112-j	U312
12-11-16	11	9	12	21	21
12-13-10-11-16
Из узла 13	j	L13-j	U2j	L113-j	U313
13-10-11-16	10	2	18	20	20
Из узла 15	j	L15-j	U2j	L115-j	U315
15-13-16
15-13-10-11-16	13	7	20	27	27

 

Полученные кратчайшие маршруты из каждого узла в узел 16 и значения их длин U³_j (выделены заливкой) занесем в таблицу 12.

5) Приближение k=4.

Определим длину L⁴_i-j возможного маршрута из i-гo узла в узел 16, проходящего через j-й узел, с числом промежуточных узлов не более четырех, как сумму расстояния L_i-jот i-го узла до j-го узла и длины U³_j маршрута из j-го узла в узел 16 с числом узлов не более трех:

L⁴_i-j= L_i-j+ U³_j, i = 1, 2, … 15, j = 1,2, … 16, j ≠ i,j ≠ 16.

В качестве длины кратчайшего маршрута из i-го узла в узел 16 принимается минимальное из возможных значений:

U⁴_j= min{L⁴_i-j}

 

Таблица 11 – Маршруты в узел 16 с числом промежуточных узлов не более четырех

Из узла 1	j	L1-j	U2j	L11-j	U31
1-7-6-11-16	7	5	33	38	38
Из узла 2	j	L2-j	U2j	L12-j	U32
2-8-13-16
2-8-13-10-11-16	8	9	30	39	39
Из узла 3	j	L3-j	U2j	L13-j	U33
3-10-11-16	10	20	18	38	38
Из узла 4	j	L4-j	U2j	L14-j	U34
4-10-11-16	10	11	18	29	29
Из узла 5	j	L5-j	U2j	L15-j	U35
5-6-11-16	6	3	24	27	27
Из узла 6	j	L6-j	U2j	L16-j